1. 簡介

OpenGL的光照是開啟真實世界的一扇窗，由於光照的引入可以帶來更大的真實場景模擬，更加強烈的視覺衝擊。

2. 光的本質

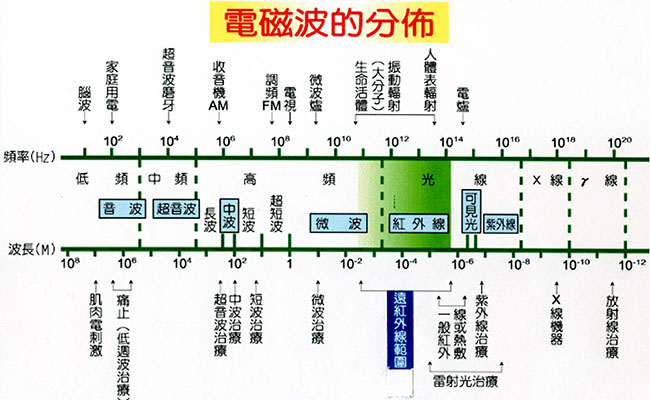
我們日常說的光實際上是狹義上的可見光，廣義上的光範圍更廣，包括了人眼不可見的紅外、紫外等，光實際是一種電磁波，電磁波圖如下所示

3. 顏色

說完了光，我們再說說顏色。現實世界中有無數種顏色，每個物體都有它自己的顏色。在計算機中我們只能通過數字模擬出有限種的顏色，儘管如此，對於人眼來說這種模擬已經足夠了。因為數字世界模擬出的顏色種類已經遠遠超過人眼的辨識極限了。在數字世界中我們通過紅、綠、藍（也稱為三原色），通過RGB的不同取值可以模擬出幾乎所有的顏色。

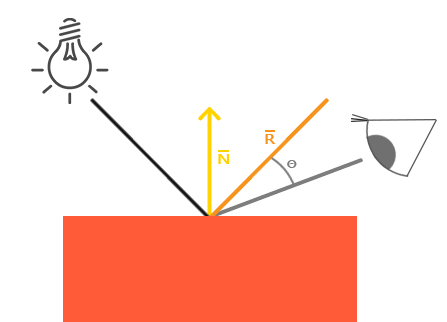
我們經常說一個物體是什麼顏色的，但是實際上物體真正並沒有那種顏色，真實情況是物體反射的顏色。物體不接受的顏色成分恰恰是它所表現的顏色。如,太陽光被認為是由許多不同的顏色組合成的白色光。如果我們將白光照在一個藍色的玩具上，這個藍色的玩具會吸收白光中除了藍色以外的所有顏色，不被吸收的藍色光被反射到我們的眼中，使我們看到了一個藍色的玩具。
下圖顯示的是一個珊瑚紅的玩具，它以不同強度的方式反射了幾種不同的顏色。

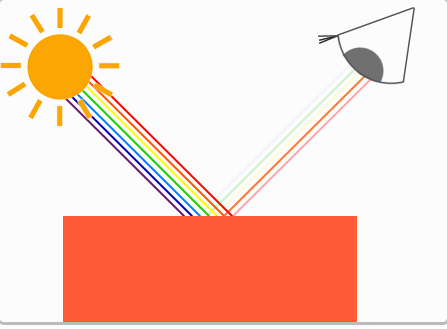
白色的陽光是一種所有可見顏色的集合，上面的物體吸收了其中的大部分顏色，它僅反射了那些代表這個物體顏色的部分，這些被反射顏色的組合就是我們感知到的顏色(此例中為珊瑚紅)。

3.1 未開啟光照的情形

在我們開始講光照之前，先了解一下未開啟光照的情況。預設情況下OpenGL並沒有開啟光照，當我們使用glColor函式設定繪製顏色的時候，我們實際上指定的是物體的最終渲染的顏色。示例程式如下：

//Legecy Code:
#pragma comment(lib, "glew32.lib")
#pragma comment(lib, "freeglut.lib")

#include <stdio.h>
#include <gl/glew.h>
#include <gl/glut.h>
#include <iostream>

int windowWidth = 0
 
;
int windowHeight = 0;

bool leftMouseDown = false;
float mouseX, mouseY;
float cameraAngleX, cameraAngleY;
float xRot, yRot;

void drawCube()
{
    // Draw six quads
    glBegin(GL_QUADS);
    // Front Face
    // White
    glColor3ub((GLubyte)255, (GLubyte)255, (GLubyte)255);
    glVertex3f(1.0f, 1.0f, 1.0f);

    // Yellow
    glColor3ub((GLubyte)255, (GLubyte)255, (GLubyte)0);
    glVertex3f(1.0f, -1.0f, 1.0f);

    // Red
    glColor3ub((GLubyte)255, (GLubyte)0, (GLubyte)0);
    glVertex3f(-1.0f, -1.0f, 1.0f);

    // Magenta
    glColor3ub((GLubyte)255, (GLubyte)0, (GLubyte)255);
    glVertex3f(-1.0f, 1.0f, 1.0f);

    // Back Face
    // Cyan
    glColor3f(0.0f, 1.0f, 1.0f);
    glVertex3f(1.0f, 1.0f, -1.0f);

    // Green
    glColor3f(0.0f, 1.0f, 0.0f);
    glVertex3f(1.0f, -1.0f, -1.0f);

    // Black
    glColor3f(0.0f, 0.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, -1.0f);

    // Blue
    glColor3f(0.0f, 0.0f, 1.0f);
    glVertex3f(-1.0f, 1.0f, -1.0f);

    // Top Face
    // Cyan
    glColor3f(0.0f, 1.0f, 1.0f);
    glVertex3f(1.0f, 1.0f, -1.0f);

    // White
    glColor3f(1.0f, 1.0f, 1.0f);
    glVertex3f(1.0f, 1.0f, 1.0f);

    // Magenta
    glColor3f(1.0f, 0.0f, 1.0f);
    glVertex3f(-1.0f, 1.0f, 1.0f);

    // Blue
    glColor3f(0.0f, 0.0f, 1.0f);
    glVertex3f(-1.0f, 1.0f, -1.0f);

    // Bottom Face
    // Green
    glColor3f(0.0f, 1.0f, 0.0f);
    glVertex3f(1.0f, -1.0f, -1.0f);

    // Yellow
    glColor3f(1.0f, 1.0f, 0.0f);
    glVertex3f(1.0f, -1.0f, 1.0f);

    // Red
    glColor3f(1.0f, 0.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, 1.0f);

    // Black
    glColor3f(0.0f, 0.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, -1.0f);

    // Left face
    // White
    glColor3f(1.0f, 1.0f, 1.0f);
    glVertex3f(1.0f, 1.0f, 1.0f);

    // Cyan
    glColor3f(0.0f, 1.0f, 1.0f);
    glVertex3f(1.0f, 1.0f, -1.0f);

    // Green
    glColor3f(0.0f, 1.0f, 0.0f);
    glVertex3f(1.0f, -1.0f, -1.0f);

    // Yellow
    glColor3f(1.0f, 1.0f, 0.0f);
    glVertex3f(1.0f, -1.0f, 1.0f);

    // Right face
    // Magenta
    glColor3f(1.0f, 0.0f, 1.0f);
    glVertex3f(-1.0f, 1.0f, 1.0f);

    // Blue
    glColor3f(0.0f, 0.0f, 1.0f);
    glVertex3f(-1.0f, 1.0f, -1.0f);

    // Black
    glColor3f(0.0f, 0.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, -1.0f);

    // Red
    glColor3f(1.0f, 0.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, 1.0f);
    glEnd();
}


void SetupRC()
{
    glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
    glEnable(GL_DEPTH_TEST);
}

void RenderScene(void)
{
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    glLoadIdentity();
    glTranslated(0, 0, -5);
    glRotated(cameraAngleY*0.5, 1, 0, 0);
    glRotated(cameraAngleX*0.5, 0, 1, 0);
    drawCube();

    glutSwapBuffers();
}


void ChangeSize(int w, int h)
{
    windowWidth = w;
    windowHeight = h;

    if (h == 0)
        h = 1;
    glViewport(0, 0, w, h);

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective(45.0, w*1.0 / h, 0.01, 1000.0f);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}


void MouseFuncCB(int button, int state, int x, int y)
{
    mouseX = x;
    mouseY = y;

    if (button == GLUT_LEFT_BUTTON)
    {
        if (state == GLUT_DOWN)
        {
            leftMouseDown = true;
        }
        else if (state == GLUT_UP)
        {
            leftMouseDown = false;
        }
    }

}

void MouseMotionFuncCB(int x, int y)
{
    if (leftMouseDown)
    {
        cameraAngleX += (x - mouseX);
        cameraAngleY += (y - mouseY);

        mouseX = x;
        mouseY = y;
    }

    glutPostRedisplay();
}


int main(int argc, char* argv[])
{
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH);
    glutInitWindowSize(800, 600);
    glutCreateWindow("OpenGL");
    glutReshapeFunc(ChangeSize);
    glutDisplayFunc(RenderScene);
    glutMouseFunc(MouseFuncCB);
    glutMotionFunc(MouseMotionFuncCB);

    GLenum err = glewInit();
    if (GLEW_OK != err) {
        fprintf(stderr, "GLEW Error: %s\n", glewGetErrorString(err));
        return 1;
    }

    SetupRC();

    glutMainLoop();
    return 0;
}

程式中通過使用glColor系列函式指定渲染最後呈現的顏色，執行結果如下：

我們通過指定每一個頂點的不同顏色，最終得到了上圖所示的效果。現在有一個問題是：我們指定的只有頂點的顏色，那兩個頂點間的顏色是怎麼計算的呢？OpenGL通過設定著色模式來達到計算指定頂點間顏色的插值。設定函式

glShaderMode(GLenum     mode)
mode:設定模式，取值有GL_SMOOTH和GL_FLAT兩種

SMOOTH插值使用的是一種線性的插值方式，如下圖所示：

vertex1和vertex2之間點的顏色是兩者顏色的線性插值。
FLAT模式僅僅使用所繪製幾何圖元最後一點的顏色來給圖元內部著色（Polygon是使用第一個點的顏色為內部著色）

3.2 開啟光照的情形

如果僅僅使用不開啟光照時候的情形，我們很難模擬真實的場景顏色。因為真實場景的顏色變幻莫測，不使用光照的模式使用的線性插值不可能模擬真實的場景。那麼究竟應該怎麼模擬呢？其實這是一個開放性的問題，每個人都可以有自己的模擬方式，都可以提出自己的演算法（但是如果使用固定管線LegacyOpenGL，你難以實現自己所想，對於可程式設計的OpenGL，你可以大膽用自己的方式來實現光照的效果）。OpenGL有自己的一套模擬方式，稱為Phong lighting model，這種模擬方式將光分成了三個成分：環境光（ambient）、散射光（diffuse）和鏡面光（specular），如下圖所示：

3.2.1 三種光成分介紹

1. 環境光：環境光不來自任何特定的方向，它來自某個光源，但是光線卻是在場景中四處反射，沒有方向可言。環境光照射的物體表面都是均勻照亮的。
2. 散射光：散射光具有方向性，來自於一個特定的方向。它根據入射光線的角度在表面均勻地反射開來。因此，如果光線直接指向物體表面，它看上去更明亮一些。如果光線是從一個較大的角度照射到物體表面，那麼它看上去顯得暗一些。
3. 鏡面光：和散射光一樣，鏡面光也具有很強的方向性，但是它的反射角度很銳利，只有沿著一個特定的方向反射。高強度的鏡面光傾向於在它照射物體的表面形成一個亮點。由於高度方向性的特點，能否被看到取決於觀察者的位置。

3.2.2 物體的材質

在OpenGL中開啟光照時，我們通過各種OpenGL的函式呼叫可以設定光的成分。當進行光照計算的時候，還需要指定物體的“顏色”。通過上面的介紹，讀者可以知道物體的“顏色”是由它所反射的光來定義的。一個藍色的球反射了光中大部分藍色的光子，並吸收其他光子。如果照射光並不包含藍色成分，那麼這個藍色的球在觀察者眼中呈現黑色。
OpenGL光照計算的時候也是使用這麼一種設定，我們並不把物體描述為具有一種特定的顏色，而是認為它由一些具有某種反射屬性的材料所組成。在指定反射屬性的時候，我們同樣也指定這種材料對於環境光、散射光以及鏡面光的反射屬性。（正好和入射光的三種成分相對應）。

4. OpenGL光照API

下文我們分析OpenGL中怎麼使用光照的API來得到光照的效果，分成兩部分介紹。

4.1 Legecy OpenGL 光照

在Legecy OpenGL中光照計算需要通過設定光的成分以及物體的材質來完成，包括如下的API

上文中的程式碼演示了一個使用glColor指定顏色的立方體，並沒有開啟光照。當我們開啟光照之後（只需要在SetupRC函式中新增一句程式碼glEnable(GL_LIGHTING);），可以發現場景完全變了，執行之後如下圖所示：

這是由於當開啟光照計算之後，glColor指定的顏色並沒有任何作用。物體的顏色是通過計算光照計算來完成的。之所以會出現暗灰色，是因為當前場景中存在這一個預設的微弱的環境光，可以通過修改glLightModel修改它。

float globalAmbient[4] = { 0.5, 0.5, 0.5, 1.0 };
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, globalAmbient);

通過修改之後物體顯得更亮了一些。當我們僅僅開啟了光照計算並沒有做任何設定的時候，OpenGL事實上使用了預設的設定。這個時候我們幾何體的材質的環境光反射RGBA值是（0.2,0.2,0.2,1.0），由於不存在其他光的成分，因此其他的材質特性不起作用。（參與計算的是光的環境光成分和物體的環境光反射成分）

4.2 Core Profile中 光照的計算公式

4.2.1 環境光計算公式

環境光的計算相對簡單，由於環境光對幾何體的每個頂點的影響都是一樣的。它僅僅將光源的環境光成分與材質的環境光成分相乘後疊加即可：計算的虛擬碼如下

光(R,G,B) x 材質(R',G',B') = (RxR', GxG', BxB')

4.2.2 散射光計算公式

當開啟光照之後，指定幾何體的散射材質，那麼計算公式如下：
散射光 x 散射材質 = 散射的顏色
當散射光照射物體表面的時候，物體表面呈現的亮度與光線的入射角有很大的關係，如下圖所示：

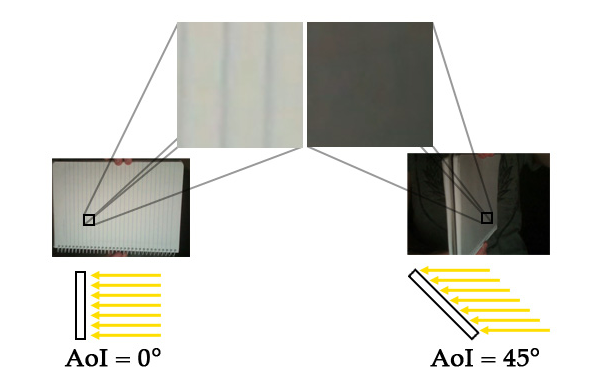
關於入射角的解釋：

也就是說入射角為0時，物體表面最亮，入射角為90度是，物體表面最暗。
如果我們以一個值來定義亮度，0.0是最暗，1.0是最亮。那麼可以簡單的定義亮度由入射角的餘弦值來表示。

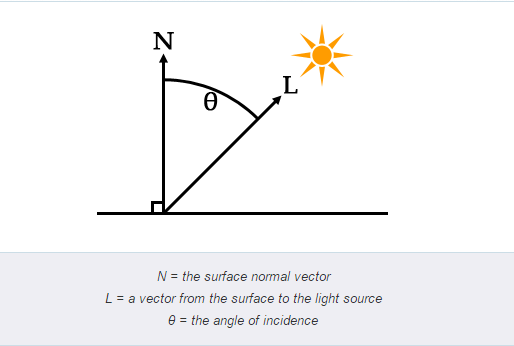
計算兩個角的餘弦值只需要獲得兩個向量單位化之後進行點乘就可以了。
也就是說，為了計算散射光，我們需要獲取兩個向量
1. 頂點的法線向量
2. 光線照射到頂點的方向
在OpenGL中使用點的法線這種方式可能有些奇怪，因為按照數學上來說，點並沒有發現，只有面才有法線。對於頂點的法線，一般來說我們需要提供一個頂點法線陣列作為頂點的屬性的輸入資料。另外也可以通過計算面個法線，並把該法線作為所有組成麵點的法線。（OpenGL中有時候為了做一些特殊的效果，常常會人為讓一個平整表面的法線不一致，這些都不在本文討論的範圍之內，日後再表），法線座標一般也是在物體的區域性座標下指定的。因為光線方向在相機座標系下計算，因此法線也必須轉換到相機座標系下。法線的轉換需要乘以法線轉換矩陣（Normal Matrix），這個矩陣是模型檢視矩陣的左上角3x3矩陣的逆的轉置，具體的推導過程可以參考：OpenGL Normal Vector Transformation

另一個需要計算的是光源到頂點的方向，一般來說光源的位置是我們在程式中指定的，那麼另一個位置是頂點的位置，頂點一般指定的是區域性座標下的位置（法線也是區域性座標下的法線方向）。在OpenGL固定管線中，當我們呼叫glLight設定光源的位置時，光源位置立刻被轉換到相機座標系中（使用模型檢視矩陣），因此光照計算都是在相機座標系中計算的。[在shader中，可以將這些計算過程放到世界座標系中進行]。

現在我們可以計算散射成分了，它的計算公式可以表示如下：

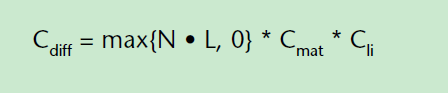
其中N是頂點單位化的法線方向，L是光線方向，Cmat是幾何體的材質中設定的散射成分，Cli是燈光中的散射光成分。

4.2.3 鏡面光計算公式

鏡面光讓物體表面看起來像鏡子一樣明亮，當光線入射時，鏡面反射的效果如下圖：

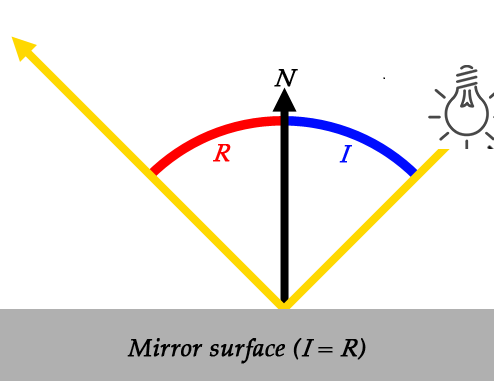
當計算鏡面光時，與計算散射光有點不同，它需要考慮觀察者的位置（相機位置），當光線完全反射到相機中時，可以看到物體表面的亮點。

計算鏡面光的過程如下：
1. 計算入射光方向
2. 計算反射光方向
3. 計算頂點到相機的方向
4. 計算反射光與頂點-相機方向的夾角
這個夾角基本上反映了鏡面光能被看到的強度，因此如何處理最後的強度是一個需要討論的問題。當角度很小是，我們看到的強度應該很大，當角度很大時，我們看到的強度應該很小。但是鏡面光不同於散射光，鏡面光的一致性很高，稍微角度大一點幾乎完全看不到它。於是這個角度怎麼設定才比較好呢？OpenGL使用了這樣一種演算法，通過計算兩者夾角的餘弦值，併為它設定一個指數項來模擬這種效果。這個指數項，是我們在固定管線中設定的shinness引數。它的效果需要根據情況自己調整。下圖是設定不同的引數的一個初步的效果：

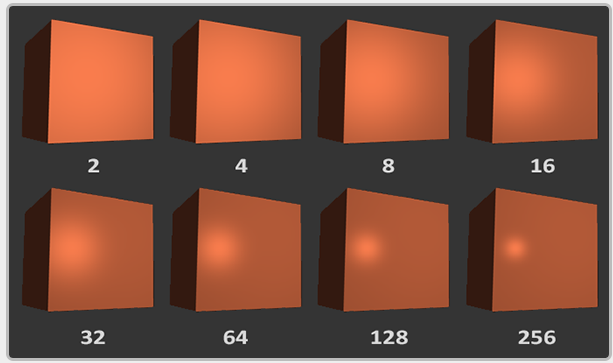
最終的演算法如下所示：

//計算入射光方向
vec3 incidenceVector = -surfaceToLight; //a unit vector
//計算反射光方向（根據入射光方向和法線方向）
vec3 reflectionVector = reflect(incidenceVector, normal); //also a unit vector
//計算頂點到相機的方向
vec3 surfaceToCamera = normalize(cameraPosition - surfacePosition); //also a unit vector
//計算頂點-相機方向與反射光方向夾角的餘弦值
float cosAngle = max(0.0, dot(surfaceToCamera, reflectionVector));
//引用鏡面光的指數（shinness）
float specularCoefficient = pow(cosAngle, materialShininess);
//計算鏡面光成分
vec3 specularComponent = specularCoefficient * materialSpecularColor * light.intensities;

4.2.4 光的衰減

在現實的光照中，當我們將光源遠離物體表面時，物體表面看起來會更暗。一般來說光線的衰減和光源到物體表面的距離的二次方成反比，也就是：

4.2.5 平行光照

平行光可以被看作是光源在無窮遠處的點光源，假設我們把這一特性應用於衰減的方程中，可以很容易知道物體表面應該越暗。這與現實情況不太相符（現實情況中我們假設太陽光是平行光，它事實上並沒有根據它距地球的距離而有所衰減）於是OpenGL中在計算平行光的時候不考慮衰減。
和點光源不同，平行光並不需要一個位置，它只有一個方向。在齊次座標中，為了表明它是一個方向，我們只需要設定它的第四維度是0就可以了。假設我們設定光源的位置在（1,0,0,0）處，也就是說光源在X軸正方向的無窮遠處，於是平行光的方向是對該值取負，也就是（-1,0,0）說明光照方向是朝著X軸負方向。
計算的演算法：只需要修改之前散射光和鏡面光的光的方向向量即可

4.2.6 聚光燈

聚光燈和點光源類似，只是有一個不同點，聚光燈的光照被限制在一個圓錐形狀內。聚光燈相比點光源多了兩個變數，第一個是圓錐形的角度，第二個是圓錐中線的方向，如下圖所示：

計算的過程只需要得到聚光燈到頂點與圓錐中線方向的夾角小於ConeAngle，就可以使用點光源的計算方法，否則就讓讓衰減量最大。

// 1. 獲取圓錐中心線的方向
vec3 coneDirection = normalize(light.coneDirection);

// 2. 獲取頂點到聚光燈燈源的方向
vec3 rayDirection = -surfaceToLight;

// 3.計算二者的角度
float lightToSurfaceAngle = degrees(acos(dot(rayDirection, coneDirection)))

// 4. 判斷是否在聚光燈照射下，如果超出，那麼衰減最大
if(lightToSurfaceAngle > light.coneAngle){
  attenuation = 0.0;
}