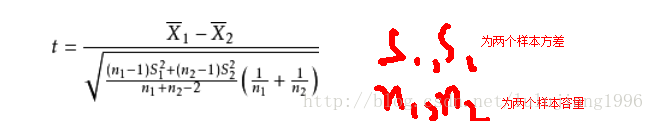機器學習筆記之R語言基礎5(T,F檢驗)
T檢驗
t檢驗分為單總體檢驗和雙總體檢驗。
單總體檢驗:【樣本平均數,總體平均數差異】
-檢驗一個樣本平均數與一個已知的總體平均數的差異是否顯著。
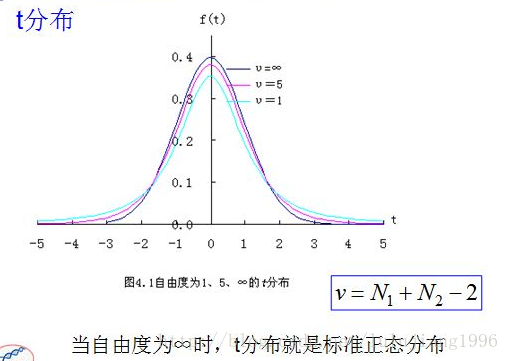
–當總體分佈是正態分佈,如總體標準差未知且樣本容量小於30,那麼樣本平均數與總體平均數的離差統計量呈t分佈。

樣本平均數計算: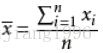
樣本標準差計算: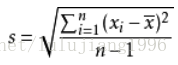
T分佈概率密度函式影象如下:
雙總體檢驗:【兩個樣本平均值間差異及樣本均值與總體差異】
-檢驗兩個樣本平均數與其各自所代表的總體的差異是否顯著。
–雙總體t檢驗又分為兩種情況,一是獨立樣本t檢驗,一是配對樣本t檢驗。
—獨立樣本t檢驗【兩個樣本平均值差異】
其統計量為:
—配對樣本t檢驗:【平均樣本與總體樣本差異】
-檢驗的物件為配對樣本的觀測值之差
-若配對樣本x1i與x2i之差為di=x1i−x2i 獨立且來自常態分配,則有以下統計量

配對樣本之差的平均數(di的平均數):
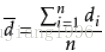
配對樣本差值的標準差:
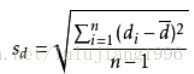
自由度:
-定義:計算某一統計量時,取值不受限制的變數個數
-df=n-k。其中n為樣本數量,k為被限制的條件數。
提問:單總體檢驗中的自由度為什麼是n-1?

假設樣本中有10個數,x1,x2,x3…x10,我們知道它的均值為5.
由於滿足公式
x1+x2+…+x9+x10=5*10
那麼,x1,x2…x9我們可以任意分配給它們數值,因為50-(x1+x2+..x9)=x10,我們只要把x10指定為需要的值就可以了,這裡面,x10受到了約束,它是不自由的,所以自由度為10-1=9.
置信區間,置信水平(置信度)
置信區間:
定義:一個概率樣本的置信區間是對這個樣本的某個總體引數的區間估計。
例如,95%置信區間:當給出某個估計值的95%置信區間為【a,b】時,可以說樣本的平均值介於a到b間的可能性為95%,而發生錯誤的概率為5%。
置信區間具體計算方式:
–置信區間下限:a=μ - Ζα/2*σ;
–置信區間上限:a=μ + Ζα/2*σ;
—-其平均值為μ,標準偏差為σ
—-α為非置信水平在正態分佈內的覆蓋面積
—-Ζα/2即為對應的標準分數
標準分數?z=(x-μ1)/σ;其中z為標準分數;x為某一具體分數(觀察值),μ1為平均數,σ為標準差。
置信水平:
定義:置信水平是指總體引數值落在樣本統計值某一區內的概率。
其中落在的某一區,指的是置信區間。
置信水平=Pr(c1<=w<=c2)=1-α
其中c1,c2為置信區間,w為實際值
α是顯著性水平(例:0.05或0.10)
100%*(1-α)指置信水平(例:95%或90%)
檢測結果怎麼看?看p值
t檢驗是對單個變數顯著性的檢驗
計算出來的p值來和顯著性水平比較,當p值小於顯著性水平是拒絕原假設,否則不拒絕原假設。
–在置信水平固定的情況下,樣本量越多,置信區間越窄
–在樣本量相同的情況下,置信水平越高,置信區間越寬。
F檢驗(聯合假設檢驗)
定義為:
F=(X/m)/(Y/n)
其中X,Y為兩個獨立的隨機變數,X服從自由度為m的卡方分佈,Y服從自由度為n的卡方分佈,這2 個獨立的卡方分佈被各自的自由度除之後的比率這一統計量的分佈。
f分佈概率密度函式影象:
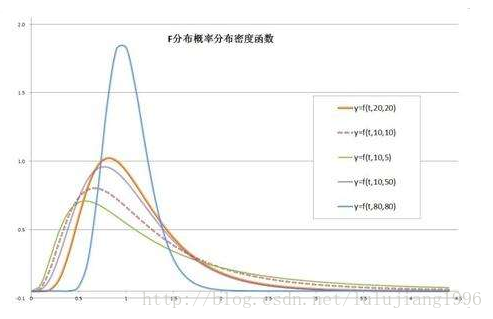
檢測結果怎麼看?
F檢驗是對所有解釋變數整體顯著性的檢驗,
只能檢測出是否有因變數的影響,但無法檢驗出具體的因變數,必須依靠t檢驗。