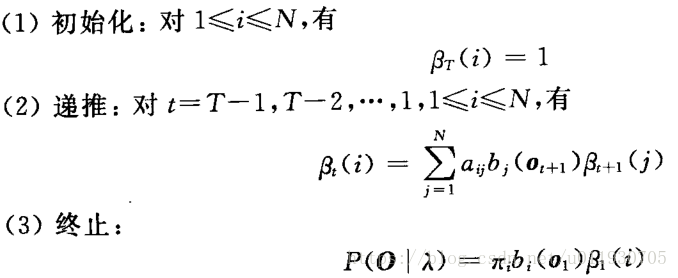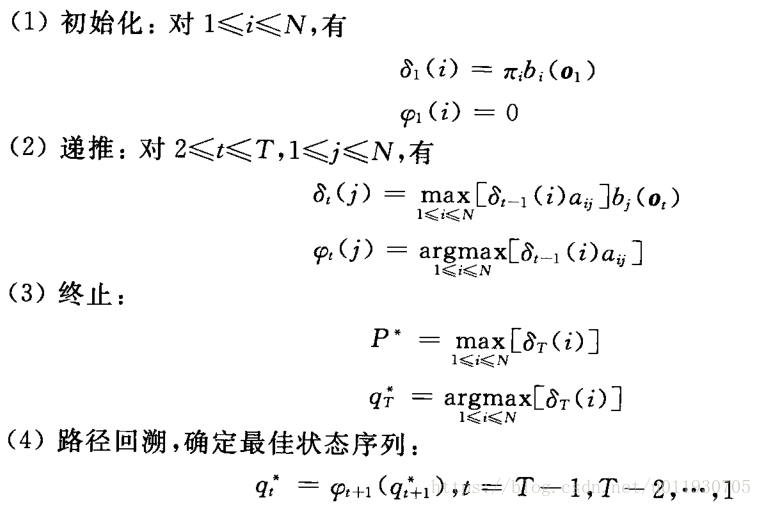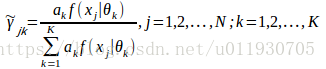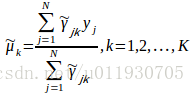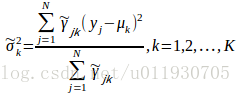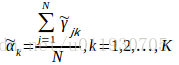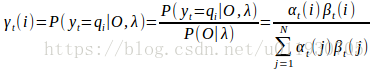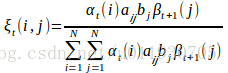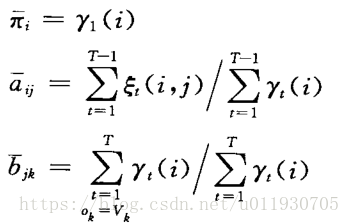1. 介紹

1. HMM在實際應用中主要用來解決3類問題。

1.評估問題(概率計算問題)

即給定觀測序列 O=O1O2…Ot和模型引數λ=(A,B,π)，怎樣有效計算這一觀測序列出現的概率P(O|λ)

2.預測問題 (也稱解碼問題)

即給定觀測序列 O=O1O2…Ot和模型引數λ=(A,B,π)，怎樣尋找滿足這種觀察序列意義上最優的隱含狀態序列S。

3.學習問題。

即HMM的模型引數λ=(A,B,π)未知，如何求出這3個引數以使觀測序列O=O1O2…Ot的概率儘可能的大,可以使用極大似然估計引數(EM演算法)。

4.個人理解

通過Baum-Welch訓練HMM模型，然後輸入需要判斷的資料通過前向後向演算法計算確定屬於哪個模型，最後通過

viterbi解碼隱含狀態序列 

1. 前向演算法

• 問題：給定觀察值序列O=o1,…,oT以及一個模型λ=(π,A,B ) 時產生出O的概率P(O|λ)？

• 前向向量定義：at(i) = P(o1 o2 …ot,qt=i|λ)

• 前向演算法過程如下：

（1）初始化：a1(i) = πibi(O1), 1≤i≤N

（2）遞推:

,1≤j≤N,1≤t≤T-1

t+1時刻狀態j的概率值為t時刻每一個狀態的概率值與其對應轉移函式相乘的累積和再與觀察值概率相乘

（3）終止:

其中：

• 下面解釋這個演算法：

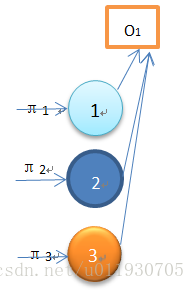
該圖為初始狀態，輸出觀察值為O1 ，圖中顯示3個狀態對應演算法初始化公式，而該序列觀察值所得概率為：

  P(O1| ）= π1b1(O1)+π2b2(O1)+π3b3(O1)=α1(1)+α1(2)+α1(3)

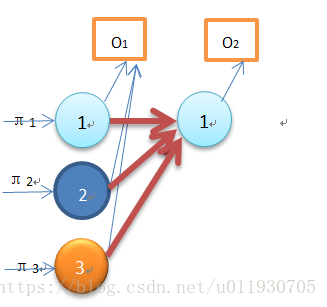
該圖為一次遞推過程，輸出觀察值為O1 O2，圖中O2對應的狀態1的概率是通過O1對應的3個狀態通過遞推公式求得，該結果為：

P(O1 O2,q2=θ1| ）= α1(1)a11b1(O2)+ α1(2)a21b1(O2)+ α1(3)a31b1(O3)

以此類推可以得到P(o1 o2 …ot|λ)

• 前向演算法計算P(O|M)過程：

step1：α1

(1) =π1b1(red)=0.2*0.5=0.1

α1(2)=π2b2(red)==0.4*0.4=0.16

α1(3)=π3b3(red)==0.4*0.7=0.21

step2：α2(1)=α1(1)a11b1(white)+α1(2)a21b1(white)+α1(3)a31b1(white)

...

step3:P(O|M) = α4(1)+α4(2)+α4(3)

前向演算法實現程式碼參考此連結：

1. 後向演算法

• 後向向量定義：βt(i) = P(ot+1 ot+2 …ot+T |qt=i,λ)

βt(i)：t時刻狀態i的概率值為t+1時刻的每個狀態與其對應的轉移函式和對應的觀察值概率相乘的累加和的值。

• 下面解釋這個演算法：

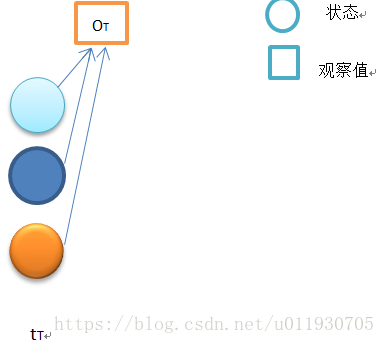
初始狀態如上圖，當t=T時，按照定義：時間t 狀態qT輸出為OT+1......的概率，由於從T+1開始的輸出是不存在的（T時刻是終止終止狀態），即T之後是空，是個必然事件，因此βt(i)=1,1≤t≤N

上圖是當t=T-1時的狀態，

βT-1(i)=P(OT|qT-1=i,λ)=ai1b1(OT)βT(1)+ai2b2(OT)βT(2)+ai3b3(OT)βT(3)

......

當t=1時，

β1(1)=P(O2O3...OT|q2=1,λ)=a11b1(O2)β2(1)+a12b2(O2)β2(2)+a13b3(O2)β2(3)

β1(2)=P(O2O3...OT|q2=2,λ)=a21b1(O2)β2(1)+a22b2(O2)β2(2)+a23b3(O2)β2(3)

β1(3)=P(O2O3...OT|q2=3,λ)=a31b1(O2)β2(1)+a32b2(O2)β2(2)+a33b3(O2)β2(3)

終止條件下：

P(O1O2...OT|λ)=π1b1(O1)β1(1)+π2b2(O1)β1(2)+π3b3(O1)β1(3)

程式例證

• 後向演算法計算P(O|M)：

step1:β4(1) = 1，β4(2) = 1 ，β4(3) = 1

step2:β3(1)=β4(1)a11b1(white)+β4(2)a12b2(white)+β4(3)a13b3(white)              

...

step3:P(O|M)=π1β1(1)b1(O1)+π2β1(2)b2(O1)+π3β1(3)b3(O1)

後向演算法示例程式碼參考下面連結：

1. Viterbi演算法

• 介紹:Viterbi演算法實際上是用動態規劃解HMM預測問題,求概率最大路徑

也就是求觀察序列的最可能的標註序列

• 問題：給定觀察值序列O=o1,…,oT以及一個模型λ=(π,A,B ) 時，如何確定最佳狀態序列Q*=q1*,q2* ,…,qT*

• 定義： 為時刻t沿一條路徑q1,q2,…qt且qt=i,產生序列O的最大概率

• 求取最佳序列Q*的過程如下：

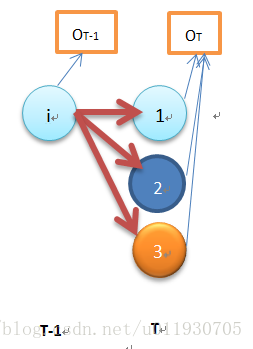
• 下面解釋這個演算法：

其中 指的是：從t-1時刻所有單個狀態路徑到達時刻t狀態為j的路徑最大概率值。

指的是： t時刻狀態為j的所有路徑中標記概率最大的第t-1個結點

程式例證

• 計算方法

step1 初始化：δ1(1)=0.2*0.5=0.1，δ1(2)=0.4*0.4=0.16，

δ1(3) = 0.4*0.7=0.28

step2 遞推：δ2(1) =max[0.1*0.5,0.16*0.3,0.28*0.2]*0.6

記錄ψ2(1)=3 來記錄到這個狀態的前一個最大可能狀態。

...

step3 終結：最佳路徑是δ4(1)δ4(2)δ4(3)最大的一個對應的狀態

step4 回溯：從最後一個狀態往回查詢路徑

示例程式碼參考下面連結：

1. EM演算法

• 最大期望演算法（Expectation Maximization Algorithm，又譯期望最大化演算法）是一種迭代演算法, 用於含有隱變數（hidden variable）的概率引數模型的最大似然估計或極大後驗概率估計。

• 演算法流程:

Step1:計算期望（E），利用概率模型引數的現有估計值，計算隱藏變數的期望，即求Q函式。

Step2:求極大值（M），利用E 步上求得的隱藏變數的期望，對引數模型進行最大似然估計， 。

終止條件：反覆迭代這兩步，直至收斂為止。

• Q函式:完全資料的對數似然函式logP(O,Q|λ)關於在給定觀測資料O和當前引數λ(i)下對為未觀測資料Q的條件概率分佈P(Q|O,λ(i))的期望成為Q函式，即 。

。

舉例說明：

假設現在有兩枚硬幣1和2，,隨機拋擲後正面朝上概率分別為P1，P2。為了估計這兩個概率，做實驗，每次取一枚硬幣，連擲5下，記錄下結果，如下：

硬幣	結果	統計
1	正正反正反	3正-2反
2	反反正正反	2正-3反
1	正反反反反	1正-4反
2	正反反正正	3正-2反
1	反正正反反	2正-3反

可以很容易地估計出P1和P2，如下：

P1 = （3+1+2）/ 15 = 0.4
P2= （2+3）/10 = 0.5

還是上面的問題，現在我們抹去每輪投擲時使用的硬幣標記，如下：

硬幣結果統計

Unknown 正正反正反 3正-2反

Unknown 反反正正反 2正-3反

Unknown 正反反反反 1正-4反

Unknown 正反反正正 3正-2反

Unknown 反正正反反 2正-3反

使用EM演算法：

先隨便給P1和P2賦一個值，比如：

P1 = 0.2

P2 = 0.7

第一輪拋擲最可能是哪個硬幣。

如果是硬幣1，得出3正2反的概率為 0.2*0.2*0.2*0.8*0.8 = 0.00512

如果是硬幣2，得出3正2反的概率為0.7*0.7*0.7*0.3*0.3=0.03087

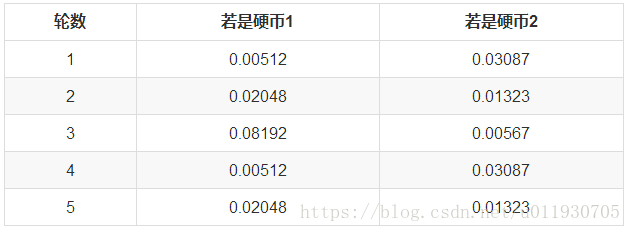
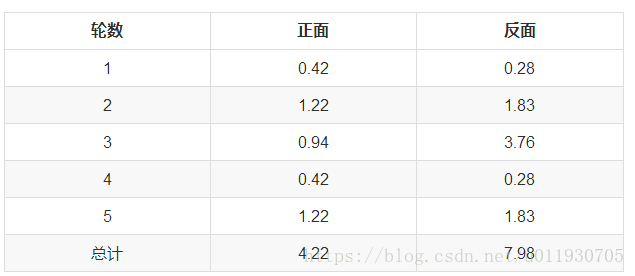
然後依次求出其他4輪中的相應概率。做成表格如下：

利用上面這個表，我們可以算出每輪拋擲中使用硬幣1或者使用硬幣2的概率。比如第1輪，使用硬幣1的概率是：

0.00512/(0.00512+0.03087)=0.14

使用硬幣2的概率是1-0.14=0.86

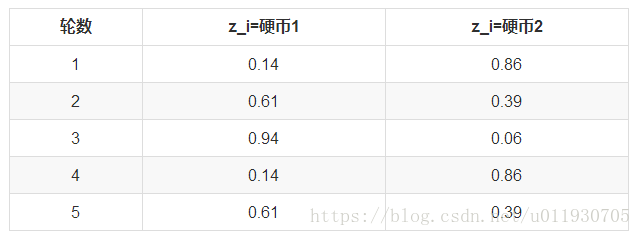
依次可以算出其他4輪的概率，如下：

這一步，我們實際上是估計出了z的概率分佈，這步被稱作E步。

我們按照期望最大似然概率的法則來估計新的P1和P2：

以P1估計為例，第1輪的3正2反相當於

0.14*3=0.42正

0.14*2=0.28反

依次算出其他四輪，列表如下：

P1=4.22/(4.22+7.98)=0.35

可以看到，改變了z值的估計方法後，新估計出的P1要更加接近0.4。原因就是我們使用了所有拋擲的資料，而不是之前只使用了部分的資料。

這步中，我們根據E步中求出的z的概率分佈，依據最大似然概率法則去估計P1和P2，被稱作M步。

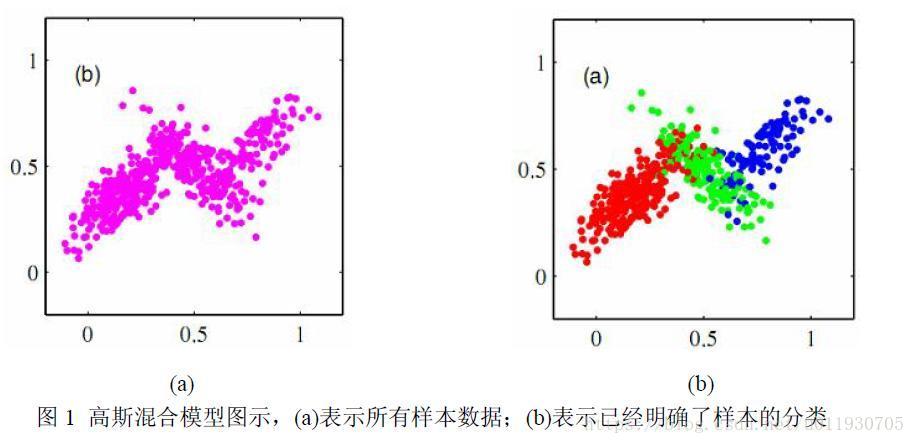
1. 高斯混合模型GMM(幾個高斯的疊加)

• 定義：高斯混合模型指具有如下形式的概率分佈模型:

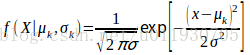
其中 是係數，且 , ; 是高斯分佈密度是第K個分模型，其中 ， 其中 中的引數可以用EM演算法估計,k的取值越大函式擬合的效果越好。

• 在HMM中每個狀態都是一個高斯混合分佈，所有狀態的觀察概率密度函式共同構成了HMM模型的引數B。通過MFCC（梅爾頻率倒譜系數）進行音素的特徵提取，是一個39維特徵。語音識別中，一個詞由多個音素組成，一個音素對應多個狀態。

• 用EM演算法可以估計高斯混合模型引數：

其中觀測資料是 ,隱含引數是選擇第幾個模型 j=1,2,…,N;k=1,2,…,T

E步:當前模型引數下第j個觀測資料來自第k個分模型的概率

M步：計算新一輪迭代模型引數

重複EM步驟訓練引數，直至收斂

• 下圖是3個分量係數的高斯混合模型。

1. Baum-Welch演算法（非監督學習方法，EM的特例）

• 給定觀察值序列O=（o1 o2 … oT）假設一個 ，其中隱資料為Y=（y1 y2 … yT）使P(O|λ)最大，通過EM演算法訓練λ引數。

，其中

• 定義 ：是給定模型λ和觀測資料O，在時刻t處於狀態qi的概率，記為

• 在觀測O下狀態i出現的期望值

• 在觀測O下狀態i轉移的期望值為

其中 推導過程如下：

由後向定義

並假設從T-1開始遞推有：

由前向定義

整理得：

以此類推可以推出：

因此可以推出該公式：

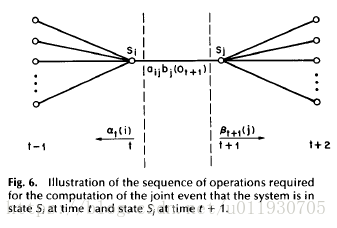
• 定義 ：是給定模型λ和觀測資料O，在時刻t處於狀態qi且在時刻 t+1處於狀態qj的概率，記為

• 在觀測O下狀態i轉移到狀態j的期望值為

其中 推導過程如下：

所以

因此：

• Baum-Welch演算法流程：

Step1：初始化，假設一個模型

Step2：E步，求 和

Step3：M步，利用E步的資料重新計算模型 引數

Step4：反覆迭代2,3步直至模型收斂。

1. 基於最大互資訊的HMM

• Baum-Wekch演算法實際是HMM的最大似然引數估計方法，即給定訓練序列O使得P(O|λ)最大，對初始模型的選定要求和經驗比較高；而最大互資訊估計在此方面優於最大似然估計，但是最大互資訊沒有前向後向演算法那樣有效的方法計算，一般只能通過最大梯度法求解。

• 對於訓練序列O和模型λ，互資訊的定義為：

1. 大詞彙連續語音識別

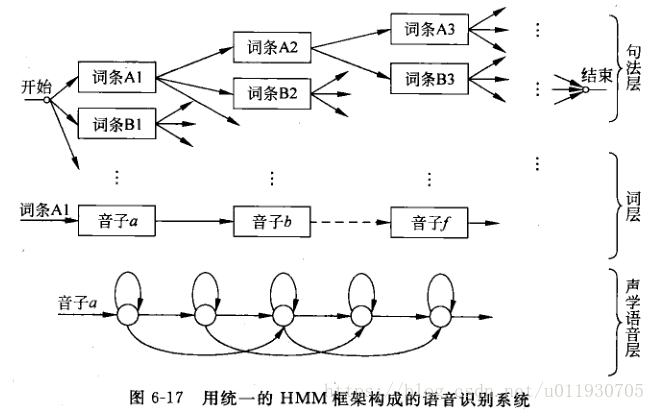
• 通過將聲學的語音層、詞層、句法層三層引入HMM框架中

1. 聲學語音層：是識別系統的底層，接收輸入語音，並以一種“子詞(subword)”為單位作為識別輸出，每個子詞單位對應一套HMM結構和引數。

2. 詞層：需要一部字典規定詞彙表中每個詞是由什麼音素-音子串接而成。

3. 句法層：規定詞按照什麼規則組合成句子。句中的一個要選擇的詞條以一定的概率出現，而選擇第二個詞條概率與前一個詞條有關，以此類推

4. 下圖描述了一個統一的HMM框架系統組成圖，從狀態出發可以逐層擴大到音子，詞，句子。

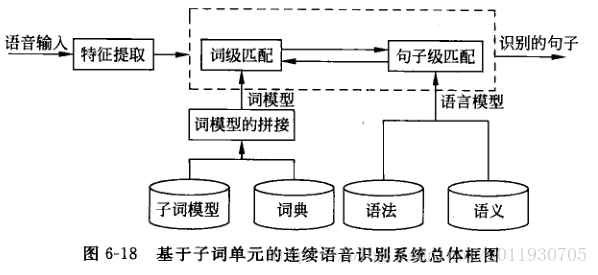
• 大詞量連續語音識別總體框架如下圖

• 聲學模型(語音識別系統底層)：設計一套HMM子詞單元模型。

1. 基本聲學單元的選擇：

1. 英語一般選擇音素。

2. 漢語選擇聲韻母：漢語是單音節，漢語的音節是聲韻結構，而且與聲母相連的只有韻母或者靜音，與韻母相連的也只有聲母或者靜音，該規則會大大減少上下文相關的聲韻母基元數量。

1. 基元的擴充套件

1. 單純的聲母韻母的音素成為上下文無關的音素，簡稱單因素。

2. 與左或右相鄰音素的相關情況選取的基元，稱為雙音素。

3. 與左和右同時相關的稱為三音素。

解決訓練資料稀疏的問題，一般對上下文相關的音素進行聚類並根據聚類進行狀態共享。有兩種方法。

1. 基於資料驅動狀態共享策略（不能處理無樣本音素）

HTK（HMM tools kit）提供了一種基於最小類合併的資料驅動聚類方法。

1. 基於決策樹狀態共享策略

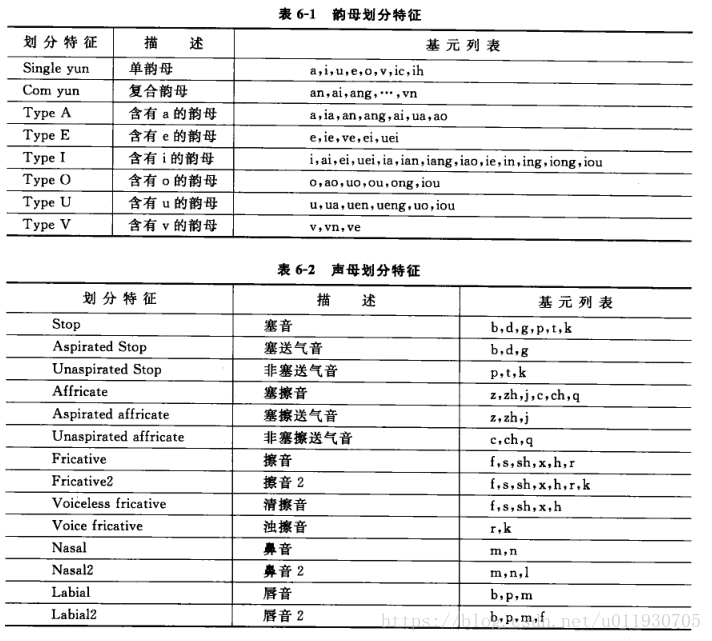
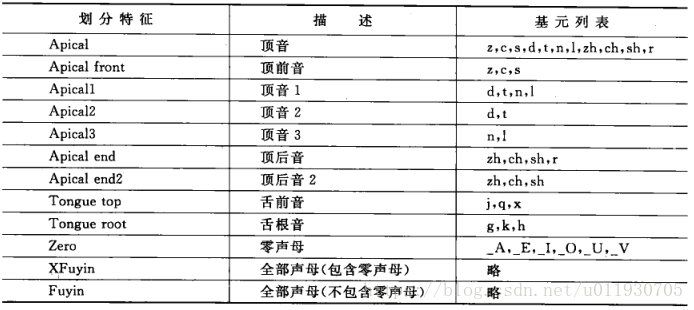
a.發音相似性：包括韻母劃分特徵、聲母劃分特徵

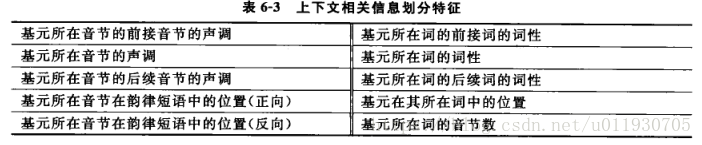
b.基元的上下文相關資訊

c.ID3決策樹演算法：從根結點開始，對結點計算所有可能特徵問題的資訊增益，選擇資訊增益最大的特徵作為結點的特徵，由該特徵的不同取值建立子結點，再對子結點遞迴呼叫以上的方法。

隨機變數熵定義：

Info（D）=

資訊增益公式：

Gain（A）=Info（D)-Info（D|A）

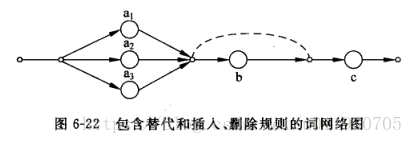
1. 聲學-語音學層之間的詞層字典用網路圖來描述（每個詞由哪些子詞以何種方式組合）

1. 聲調處理：有一種方法可以將韻母細化從而回避此問題。

1. 基於子詞單元的HMM訓練

一般採用從左到右的結構，狀態數固定2-4個。每個語音段中包含多個子詞單元，因為一個足夠大的訓練集每個子詞單元都可以出現很多次。

使用分段K均值演算法產生最佳模型：

1. 初始化：將每個訓練語句線性分割成子詞單元，將每個子詞單元線性分割成狀態。（每個語句子詞單元和內部狀態駐留時間是均勻的）

2. 聚類：每個給定子詞單元的每個狀態，在所有訓練語句段中用特徵向量用k均值演算法聚類。

3. 引數估計：根據聚類結果計算均值，各維方差和混合權值係數。(GMM)

4. 分段：根據上一步得到的新的子詞單元模型通過viterbi演算法對所有訓練語句再分成子詞單元和狀態，重新迭代聚類和引數估計，直到收斂。

1. 其他語音相關

• HMM孤立詞識別過程：

1. 首先通過HMM訓練演算法（Baum-Welch）為系統詞彙表的每個詞建立對應的模型λi。

2. 然後通過前向後向演算法或Viterbi演算法求出哥哥概率P(O|λi)值，其中O為待觀察值的觀察值序列。

3. 最後在後處理階段，選取最大的概率值所對應的詞為O的識別結果。

• 在孤立詞語音識別中，最為簡單有效的方法是採用DTW(Dynamic Time Warping，動態時間歸整)演算法，該演算法基於動態規劃(DP)的思想，解決了發音長短不一的模板匹配問題，是語音識別中出現較早、較為經典的一種演算法，用於孤立詞識別。HMM演算法在訓練階段需要提供大量的語音資料，通過反覆計算才能得到模型引數，而DTW演算法的訓練中幾乎不需要額外的計算。所以在孤立詞語音識別中，DTW演算法仍然得到廣泛的應用。

• 連線詞識別（窮舉法很難實現）動態規劃。