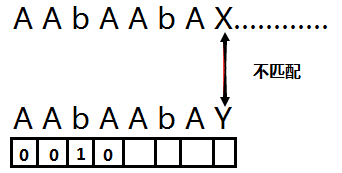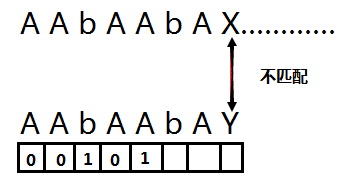問題：

已知字串 B 是字串 A 的一個子串,問字串 B 在字串 A 的第一次出現位置. 

暴力方法:從 A 字串 的每個位置開始對字串 B 進行匹配. 這種方法根據資料的不同 複雜度不同最高可以達到 O( m*n ).   (m,n分別為兩個字串的長度)

KMP演算法：  

我們先來看普通的暴力方法在對下面的匹配過程:

這個匹配過程到達 X,Y 處發現不匹配,按照暴力方法我們就把下面的字串向右移動一個字元然後繼續跟A進行匹配.但是實際上看圖我們就可以知道移動一個字元肯定還是無法匹配成功, 而這樣的一步一步的移動也是十分費時.那麼我們就要找到最佳的右移長度.

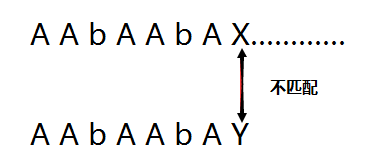
看這幅圖：

假如在匹配d和b的時候失敗了,我們移動 a 到 A  對應的位置 , 那麼就要滿足 AB 段和 ab段匹配 ,又因為 cd 和 AB 段已經匹配上了, 實際上就是要 ab 段和 cd 段匹配.我們要移動最長距離就要保證 ab  和 cd 在匹配上的同時, ab 串的長度最大值.那麼就可以直接把 a 移動到 A 進行匹配.換句話就是求 下面那個字串在 ad 段部分的首尾匹配子串的最大長度.

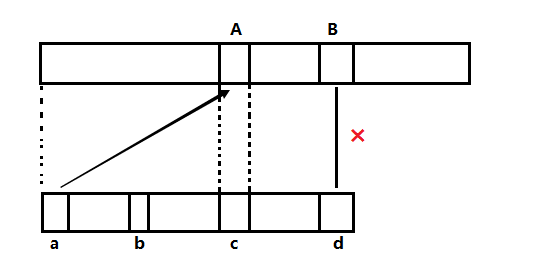
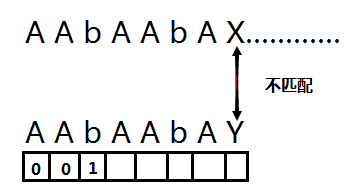
這個時候我們引入一個數組 c [ i ]  表示 下面的待匹配的子串在 0 ~ i-1 部分的首尾匹配子串的最大長度.初始化前面兩個為0.

然後上下開始匹配,匹配到 b 的時候我們先計算下面陣列的值,計算方法是看前一個位置的陣列的值,這裡 b 的前面一個位置的值是0,那麼就比較前一字元與0位置字元是否相等.如果相等,當前陣列值就等於前一陣列的值加1,如果不相等當前陣列值就等於0.

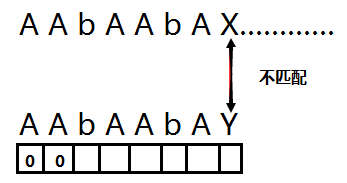
現在我們就遞推到b 發現  b 前面的字元和 0字元相同都為 A 那麼  b 下面對應的陣列的值為 0+1=1;

繼續遞推,到 A  ,前一陣列的值 為 1 , 那麼我們比較前一字元與 1 位置的字元 一個是 b ,一個是 A.那麼 A對應下面的陣列值為 0;

繼續遞推到 A ,前一陣列的值為 0 , 那麼我們比較前一字元與 0 位置的字元, 兩個都是A 那麼 當前A下面對應的陣列值為0+1=1

繼續匹配……

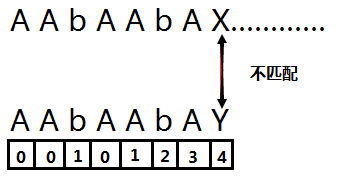
直到算完 Y 下面的陣列的值後發現 上下不匹配, 我們找 Y下面的值 4, 然後從 4 號 位置的字元 與上面字串的 X進行匹配,如果相同就繼續重複以上操作.如果不相同那麼繼續呼叫4 號位置的字元下面的陣列的值 0 ,然後用 0位置的元素和 X 比較.相同繼續向後匹配,如果不同就繼續呼叫下面的陣列………………(注意:如果0

位置的字元也無法匹配 X 那麼不用呼叫0號位置字元下面的陣列的值,而是繼續用0號位置的字元比較上面 X 後面的一個字元……)

結束:如果下面的字串的最後一個字元也匹配成功那麼, 上面字串的匹配成功的最後一個字元位置減去下面字串的長度再加1 就是下面字串出現在上面字串的第一次位置.

程式碼：

#include <stdio.h>
#include <string.h>
char str1[100],str2[10]; //str2是str1的子串.
int k,c[10],ans;
void kmp(int t1,int t2)
{
	if(str2[t2]=='\0'){           //先判斷是否匹配完
		ans=t1-t2;
		return;
	}
	if(t2>1&&c[t2]==-1){         //繼續計算當前字元下面的陣列的值.
		if(str2[t2-1]==str2[c[t2-1]]) c[t2]=c[t2-1]+1;
		else c[t2]=0;
	}
	if(str1[t1]==str2[t2])      // 如果當前字元匹配成功,繼續向後匹配.
		kmp(t1+1,t2+1);
	else if(t2==0)              // 如果當前字元匹配失敗,但是下面的字元位置是0,那麼上面字元向後移動一個繼續匹配.
		kmp(t1+1,t2);
	else                       // 如果當前字元匹配失敗,但是下面字元的位置不是0,那麼呼叫當前字元下面c陣列的值進行匹配
		kmp(t1,c[t2]);
}
int main()
{
	while(scanf("%s%s",str1,str2)!=EOF){
		memset(c,-1,sizeof(c));
		c[0]=c[1]=0;  //初始化c陣列.
		kmp(0,0);
		printf("%d\n",ans+1);
	}
	return 0;
}

時間複雜度在 O(n)~O(n+m) 之間,  注意：n 為 str1 的長度