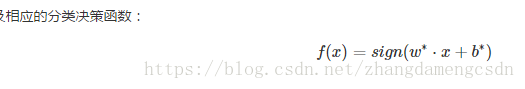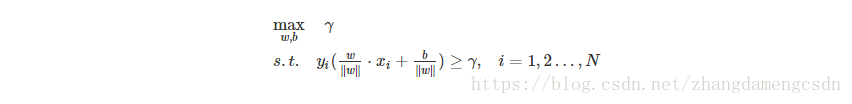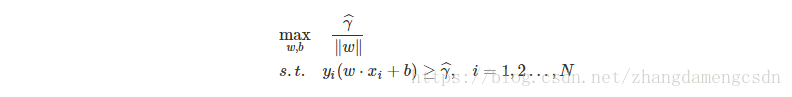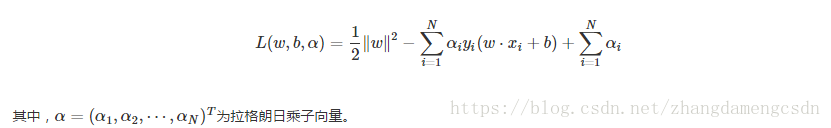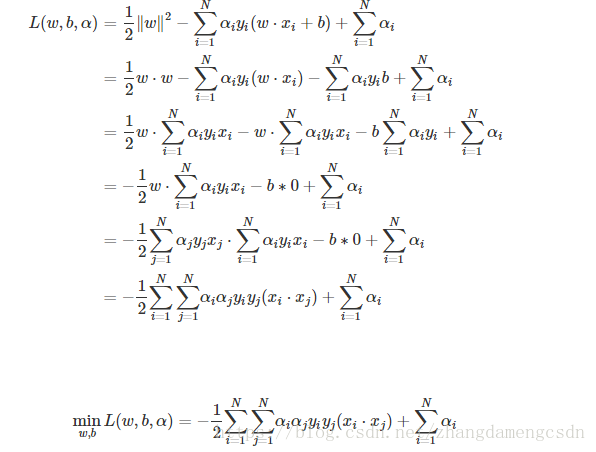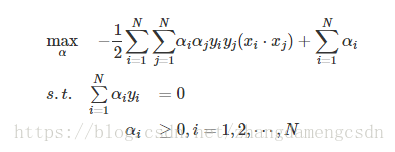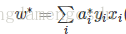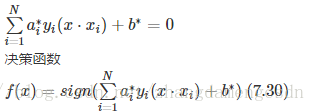令人煎熬的SVM 線性可分支援向量機與硬間隔最大化
此時此刻,還是帶著問題寫的部落格····
哇,怎麼總結.
先貼上一個部落格地址 http://blog.pluskid.org/?p=632
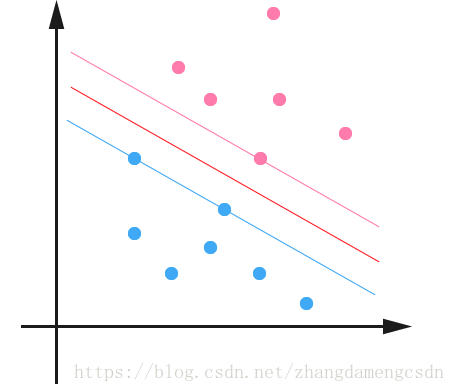
先說名字,線性可分,就是存在一個超平面,能把正例跟負例完全分隔開,那麼這個資料集就是線性可分的。
支援向量:離超平面越近的越難分是正例還是負例,要想加新的點以後預測更準確,就要使得 樣本點到超平面的最小距離l最大 (距離越大越容易分類)而這個能得到最小距離l的樣本點就叫做支援向量。支援向量一定是正負例都有的,它是平行於超平面,到超平面的距離為l的兩個超平面上的樣本點。
硬間隔:過支援向量的兩個超平面之間形成了一個間隔。這兩個超平面叫間隔邊界。
與軟間隔對應,硬間隔是存在於資料集線性可分的情況下,而軟間隔是資料集近似線性可分情況。後面還沒複習到,複習到再回來補充。補充:硬間隔是把所有的樣本點正確分在超平面兩側,而軟間隔允許某些樣本點錯誤分類。
然後目標函式是什麼?
要求的分離超平面是:
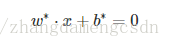
顯然要求的引數有兩個,怎麼求引數呢?
硬間隔最大化
有兩個間隔
1.函式間隔
2.幾何間隔
函式間隔,在二維空間中可以理解為點到直線的距離,點代入直線方程,然後取絕對值。
(hat gamma)
y取值正負1,乘以y,相當於取絕對值。
幾何間隔。因為如果已經選定了支援向量,對w和b成比例增長,比如都乘以2,超平面沒有變,但是這個最小間隔求出來就也變成了2倍。所以,進行規範化,就有了幾何間隔。
那麼硬間隔最大化當然是選擇幾何間隔了。
接下來是最大化。
用函式間隔是
函式間隔為什麼取1?其實沒有懂。
這是目標函式
剩下的就是如何求解上式。
這是個凸二次規劃問題。哇什麼鬼?就是符合某些條件的約束最優化問題,這個不重要。
怎麼解呢?
用到的是拉格朗日對偶性,簡單說,就是把這個問題轉換為一個比較容易求解的對偶問題。
首先構建拉格朗日函式,這個大學學過,就是把約束條件乘個因子,寫到目標函式後面。
這個拉格朗日乘子的元素都是非負的。為啥?
(1)求極小值,利用偏導
求出了w,帶回式子。
(2)然後是求極大值
也就是
這裡KKT還沒有看懂
容易求得
標黃的式子,當alpha>0,那麼中括號中的式子就等於零,也就是說,這個樣本點為支援向量;同理,當中括號中大於零,也就是非支援向量,這種時候,alpha必須等於零。(這裡被問到說,如果alpha跟括號中都等於零,你該怎麼解釋?)
因此,SVM跟邏輯迴歸的不同就在於,不用考慮那麼多點,只看少量的支援向量就夠了。
alpha向量中一定有至少一個元素大於零,為啥呢?因為如果全都為零,那麼w=0,而這顯然不是目標函式的解?哈?為啥不是?https://www.zhihu.com/question/269619107/answer/349429844
當上面情況成立,那麼就可以得到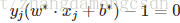
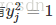
然後分離超平面即,
由此看出,決策函式只與輸入x與樣本的內積有關。
剩下的問題就是如何求解alpha,始終沒有提到。
總結一下這個演算法:
(1)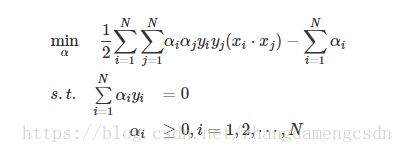
(2)求w,b
這麼多問題,什麼時候來填坑???