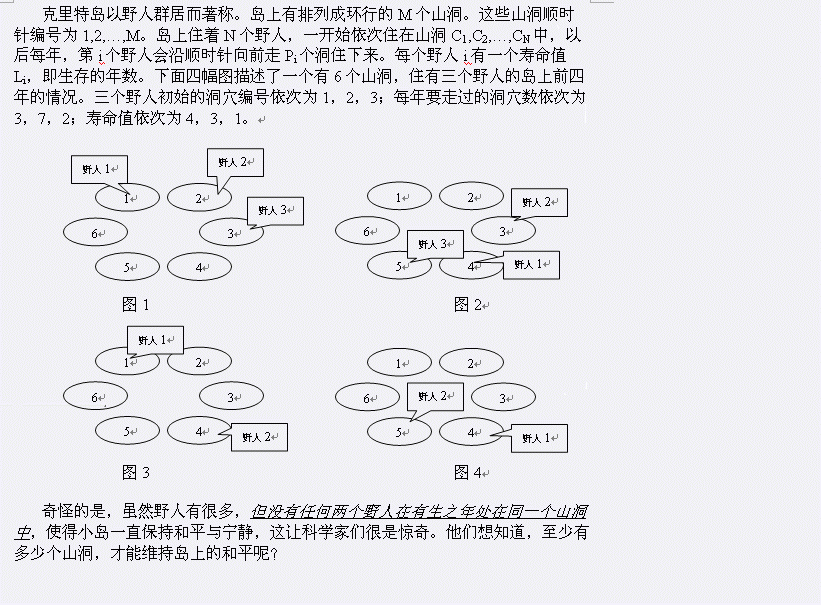
Input
第1行為一個整數N(1<=N<=15)，即野人的數目。
第2行到第N+1每行為三個整數Ci, Pi, Li表示每個野人所住的初始洞穴編號，每年走過的洞穴數及壽命值。
(1<=Ci,Pi<=100, 0<=Li<=10^6 )
Output

僅包含一個數M，即最少可能的山洞數。輸入資料保證有解，且M不大於10^6。
Sample Input
3

1 3 4

2 7 3

3 2 1
Sample Output
6

//該樣例對應於題目描述中的例子。

野人不會再想同的位置，那也就表明不會出現下列情況：（R表示一整圈的長度。）

$(C_i+P_i*t)-(C_j-P_j*t)≡0（Mod \ \ R）$

那麼移項可得

$(P_i-P_j)*t≡C_j-C_i（Mod \ \ R）$

我們可以用擴充套件歐幾里得算出下面式子裡的$T$

$(P_i-P_j)*T≡gcd(P_i-P_j,R)（Mod \ \ R）$

那麼根據性質，$T$

∗(Cj−Ci)/gcd(Pi−Pj,R)T*(C_j-C_i)/gcd(P_i-P_j,R)就是$t$的一組解。並且$T*(C_j-C_i)/gcd(P_i-P_j,R)+x*R/gcd(P_i-P_j,R)$就是$t$的解集、

如果這個解集的最小正解大於$min(l_i,l_j)$，說明當圈長為$R$時，這兩個人不會發生矛盾。

當然方程無解也不會發生矛盾，根據裴蜀定理，無解的情況就是$($

Cj−Ci)%gcd(Pi−Pj,R)!=0(C_j-C_i)\%gcd(P_i-P_j,R)!=0

至於上面那個解集的證明，詳情請看這篇部落格

#include<bits/stdc++.h>
using namespace std;
int read(){
    char c;int x;while(c=getchar(),c<'0'||c>'9');x=c-'0';
    while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x;
}
int n,Max,Min[18][18];
struct node{
    int c,p,t;
}F[18];
void exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1;y=0;return;
    }
    exgcd(b,a%b,y,x);
    y-=a/b*x;
}
int gcd(int x,int y){
    return y?gcd(y,x%y):x;
}
int check(int x,int y,int Md){
    int xx=F[x].p-F[y].p;
    int a=0,b=0,c=gcd(xx,Md);
    int yy=F[y].c-F[x].c;
    exgcd(xx,Md,a,b);
    if(yy%c) return 0;
    a=a*yy/c;c=abs(c);a=(a%(Md/c)+(Md/c))%(Md/c);
    return (a>Min[x][y])^1;
}
int main()
{
    n=read();int i,j,k;
    for(i=1;i<=n;i++){
        F[i].c=read();F[i].p=read();F[i].t=read();
        Max=max(Max,F[i].c);
    }
    for(i=1;i<=n;i++)
     for(j=i+1;j<=n;j++) Min[i][j]=min(F[i].t,F[j].t);
    for(k=Max;k<=1000000;k++){
        int flag=0;
        for(i=1;i<=n;i++){
         if(flag) break;
         for(j=i+1;j<=n;j++){
          flag|=check(i,j,k);
          if(flag) break;   
          }
        }
        if(!flag){
            printf("%d",k);break;
        }
    }
    return 0;
}