(多項式)因式分解定理(Factor theorem)與多項式剩餘定理(Polynomial remainder theorem)(多項式長除法)
阿新 • • 發佈:2019-02-07
(多項式的)因式分解定理(factor theorem)是多項式剩餘定理的特殊情況,也就是餘項為 0 的情形。
0. 多項式長除法(Polynomial long division)
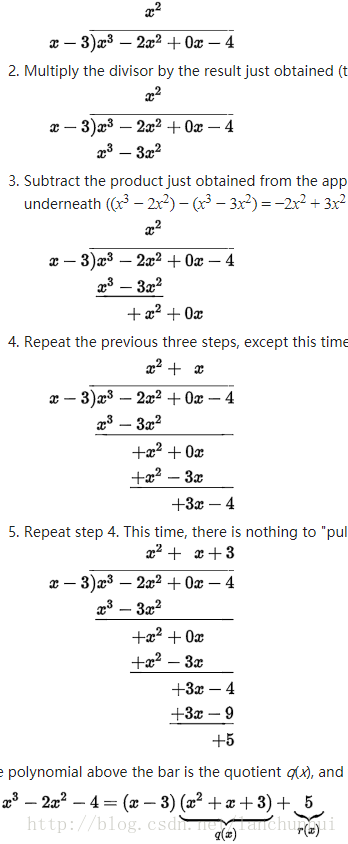
1. 因式分解定理
該定理表達的是,多項式
對於多項式
x−1 是否為其因子?f(1)≠0 x+1 是否為其因子?f(−1)=0 ,故為其因子;
(多項式除法)又有
2. 多項式餘項定理
舉例對於多項式
更為一般地,對於二次多項式
所以:
