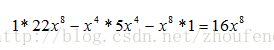Hdu 4658 要求拆分的數中每個數出現的次數不能大於等於k次，則

已經求得，現在看Q(x^k)會怎麼樣

例如，當n=8，k=4時

滿足指數為8的乘積之和為：

所以將8拆分的數中每個數的個數小於4的有16個，分別為

8,1+7,1+1+6,1+1+1+5,6+2,1+5+2,1+1+4+2,1+1+1+3+2,4+2+2,1+3+2+2,1+1+2+2+2,1+1+3+3,1+4+3,5+3,2+3+3,4+4

我的程式碼

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<set>
#include<map>
#include<list>
#include<queue>
#include<vector>
#define tree int o,int l,int r
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define lo o<<1
#define ro o<<1|1
#define ULL unsigned long long
#define LL long long
#define UI unsigned int
#define inf 0x7fffffff
#define eps 1e-7
#define M 1000000007
#define N 100001
using namespace std;
int T,n,m,k,t,maxv;
int p[N];//LL超時！
void init()
{
    p[0]=p[1]=1;
    for(int i=2; i<N; i++)
    {
        for(int j=1,k=1;; j++,k=-k)
        {
            int s=j*(j*3-1)/2;
            if(i-s>=0)
                p[i]=(p[i]+p[i-s]*k)%M;
            else
                break;
            s=j*(j*3+1)/2;
            if(i-s>=0)
                p[i]=(p[i]+p[i-s]*k)%M;
            else
                break;
        }
        while(p[i]<0)p[i]+=M;//WA!!!
    }
}
int solve()
{
    int ans=p[n];
    for(int j=1,sign=-1;; j++,sign=-sign)
    {
        int s=j*(j*3-1)/2;
        if(n-s*k>=0)//多乘以k
            ans=(ans+p[n-s*k]*sign)%M;
        else
            break;
        s=j*(j*3+1)/2;
        if(n-s*k>=0)
            ans=(ans+p[n-s*k]*sign)%M;
        else
            break;
    }
    while(ans<0)ans+=M;//WA!!!
    return ans;
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("ex.in","r",stdin);
#endif
    int ncase=0;
    scanf("%d",&T);
    init();
    while(T--)
    {
        scanf("%d%d",&n,&k);
        printf("%d\n",solve());
    }
    return 0;
}