約瑟夫環O(N)和O(M*N)演算法詳解
問題描述:
已知n個人(以編號1,2,3…n分別表示)圍坐在一張圓桌周圍。從編號為1的人開始報數,數到m的那個人出列;他的下一個人又從1開始報數,數到m的那個人又出列;依此規律重複下去,直到圓桌周圍的人全部出列,求最後一個出列人的編號。
該問題可以用陣列或者迴圈連結串列模擬,因為都是直接模擬,需要迴圈n次,每次數m次,所以時間複雜度都是O(n*m)。雖然複雜度比O(n)大,但是可以求出出圈的編號順序。也正是因為該方法將每次出圈的人都找了出來,所以做了很多無用操作,複雜度才會高達O(n*m)。
下面是陣列和連結串列方法的程式碼:
題意:n個人,從第k個人開始數1,數到m的人剔除,輸出剔除的順序。
#include <iostream>
#include<cstdio>
#include<ctime>
#include<algorithm>
#include<cstdlib>
using namespace std;
#define MAXN 10000
int a[MAXN];
int N,k,m;
bool InCircle[MAXN];
typedef struct _node{
struct _node* prev;
struct _node* next;
int number;
}node;
node* MakeDLL(int O(n)方法運用動態規劃,或者說遞推,或者說找規律,都行吧。雖然複雜度低,但是不能求出出圈的順序。如果需要求出出圈的順序,複雜度依然是O(n*m)。
該方法遞推公式網上很多都能找到,但是卻極少人給出遞推過程。
我們發現,當從圈出來一個人之後,後一個人需要從1開始重新計數直到計到m。例如有n個人(1,2,3,… ,n-2,n-1),第m個人出來之後,需要從第m+1開計數。如果從m+1個人重新編號(即m+1個人編號為0,m+1為2,… …),那麼對剩下的n-1個人的操作跟開始有n個人的時候操作就是一樣的。
這就是可以運用動態規劃的原因:n的情況跟n-1的情況存在著某種關係。而我們只需用動態方程將這種關係表達出來,問題就可以解決。
下面顯示瞭如何進行重新編號:
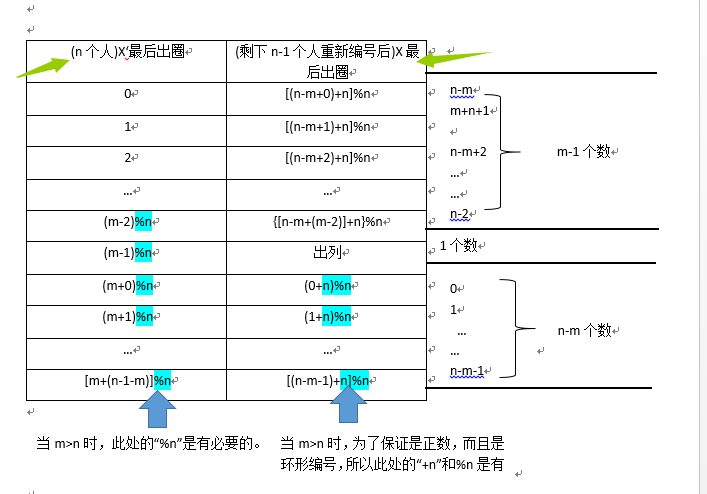
設n個人圍成一個圈的時候出列是第X’號,n-1個人圍成一個圈的時候出列的是X號,並假設X已經求出來,那麼根據上面的遞推公式就可以反推求X’: 因為X=(X’*n+n-m)%n=X’*n%n+n%n-m%n=X’-m%n
所以X’=X+m%n=(X+m)%n
如果定義:dp[n]表示圈裡有n個人的時候最後剩下那個人的編號,答案就是dp[n]。
那麼就有dp[n]=(dp[n-1]+m)%n
但是dp[n-1]並不知道,所以dp[n]也沒法求出。當然dp[n-1]也需要通過動態方程求出:
dp[n-1]=(dp[n-2]+m)%n。
同樣dp[n-2],dp[n-3]….分別需要用dp[n-3],dp[n-4]求出。
最後dp[2]需要dp[1]求出,然而dp[1]=0是已知的。
所以從dp[2]開始依次可以求出dp[2],dp[3],dp[4]…dp[n]。
那麼問題就解決了。
#include <iostream>
#include<cstdio>
#include<ctime>
#include<algorithm>
#include<cstdlib>
using namespace std;
#define MAXN 10000
int dp[MAXN];
int joseph(int m, int n) {
dp[1] = 0;
for(int i = 2; i <= n; i++){
dp[i] = (dp[i-1] + m) % i;
}
return dp[n];
}
int main(){
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
int m, n;
cin >> m >> n;
cout << joseph(m, n) << endl;
}