本人蒟蒻一隻……近日終於弄懂了可持久化線段樹的一些東西……寫下來分享一下=w=

    首先要談可持久化線段樹，你肯定得懂線段樹吧。這裡就不提線段樹了……可持久化線段樹是什麼東西呢？就是對線段樹的葉子節點做m次修改，同時做n次詢問，但這些詢問會問你的東西是做了第i次修改時XXXXX。舉個例子，給你一列數，a1,a2,a3...an，給定兩種共m個操作：1、修改一個數的值；2、詢問做了第k次修改後，第i到第j個數中最大的是多少(保證已經做了至少k次修改)。(n<=100000，m<=100000)

    如果無視掉第二個詢問的第一句話(第k次修改後)，那麼題目還是很水的啦=w=，不過加上似乎就有些問題了。但我們可以用一個笨辦法！什麼呢？就是把以前所有線段樹的版本全部都記錄下來。這樣查詢複雜度和以前不變，時間什麼的還是有保證的！

    但很可惜，這樣你要存m棵線段樹，每棵線段樹至少要2n個節點，那麼2*100000*100000個節點……早就不知道空間炸到哪裡去了=w=。

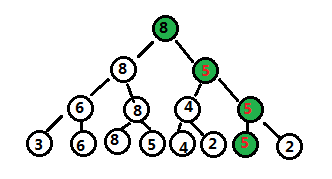
    所以我們需要更優秀的辦法。仔細觀察我們就會發現，每次修改一個節點的權值，其實所涉及到的節點最多也就一條鏈(修改ai的權值，影響的最多也就是ai，ai的fa……)，而其它所有節點的權值都沒有變。比如下圖序列36854252，如果修改了5的權值，那麼它最多能夠影響的是以綠色為底的一條鏈。(下圖直接用左右兒子點權較大的代替當前節點點權)

    那麼我們新開一棵樹存白色的節點就完全沒有意義了。所以對於每一個節點，我們用連結串列的方式將其儲存下來。每一次修改我們新建一條鏈，同時將根節點儲存下來，然後按順序修改。什麼意思呢？就是root[i]，表示第i次修改後的根節點，若上圖，假設5被修改了(比如本來是3)，root[i]=8的左兒子節點存的就是root[i-1]的左兒子節點(也是8)，它的右兒子就是新的節點5，而5的左兒子又是root[i-1]中root=8的右兒子的左兒子4，而5的右兒子是新的節點5……直到完全建成這樣一條鏈，而我們新開的節點其實也就logn個。這樣空間上就有了保證。

    不會連結串列的都給我面壁思過去=w=

    ……好吧是我太弱了，只會搞連結串列……(當然用陣列模擬連結串列也是非常茲詞的=w=)