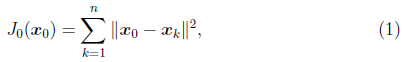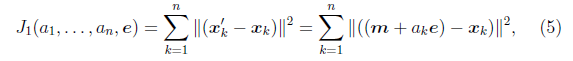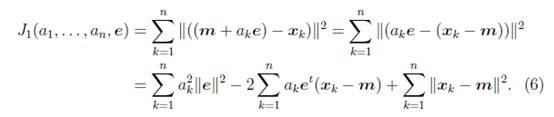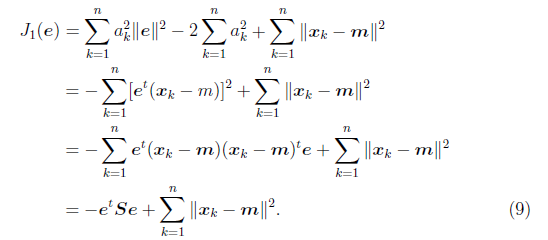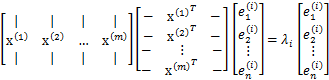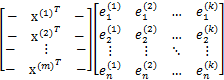系統學習機器學習之維度歸約(完整篇)
這裡,我們討論特徵選擇和特徵提取,前者選取重要的特徵子集,後者由原始輸入形成較少的新特徵,理想情況下,無論是分類還是迴歸,我們不應該將特徵選擇或特徵提取作為一個單獨的程序,分類或者回歸方法應該能夠利用任何必要的特徵,而丟棄不相關的特徵。但是,考慮到演算法儲存量和時間的複雜度,或者輸入不必要的特徵等原因,還是需要降維。較簡單的模型在小資料上更為魯棒,有小方差,模型的變化更依賴於樣本的特殊性,包括噪聲,離群點等。同時,低緯度描述資料,方便我們隊資料繪圖,視覺化分析資料結構和離群點。
降低方法,一般為特徵選擇,特徵提取,按監督和非監督分:
非監督:PCA、FA ,LLE
監督:LDA,MDS
其中,PCA,FA,MDS,LDA,都是線性投影方法,非線性維度規約有等距特徵對映,區域性線性嵌入LLE。
維度歸約使用資料編碼或變換,以便得到原資料的歸約或“壓縮”表示。如果原資料可以由壓縮資料重新構造而不丟失任何資訊,則該資料歸約是無損的。如果我們只能重新構造原資料的近似表示,則該資料歸約是有損的。有一些很好的串壓縮演算法。儘管它們通常是無損的,但是隻允許有限的資料操作。
一.先說特徵選擇,即子集選擇。
在子集選擇中,我們選擇最佳子集,其含的維度最少,但對正確率的貢獻最大。在維度較大時,採用啟發式方法,在合理的時間內得到一個合理解(但不是最優解)。維度較小時,對所有子集做檢驗。
有兩種方法,向前選擇,即從空集開始逐漸增加特徵,每次新增一個降低誤差最多的變數,直到進一步新增不會降低誤差或者降低很少。同時,可以用浮動搜尋,每一步可以改變增加和去掉的特徵數量,以此來加速。
向後選擇中,從所有變數開始,逐個排除他們,每次排除一個降低誤差最多的變數,直到進一步的排除會顯著提高誤差。如果我們預料有許多無用特徵時,向前選擇更可取。
在兩種情況下,誤差檢測都應在不同於訓練集的驗證集上做,因為我們想要檢驗泛化準確率。使用更多的特徵,我們一般會有更低的訓練誤差,但不一定有更低的驗證誤差。
像人臉識別這樣的應用中,特徵選擇不是很好的降維方法,因為個體畫素本身並不攜帶很多識別資訊,攜帶臉部識別資訊的是許多畫素值的組合。這可以用特徵提取來歸約。
二. 主成分分析(PCA)
1. 問題
真實的訓練資料總是存在各種各樣的問題:
1、 比如拿到一個汽車的樣本,裡面既有以“千米/每小時”度量的最大速度特徵,也有“英里/小時”的最大速度特徵,顯然這兩個特徵有一個多餘。
2、 拿到一個數學系的本科生期末考試成績單,裡面有三列,一列是對數學的興趣程度,一列是複習時間,還有一列是考試成績。我們知道要學好數學,需要有濃厚的興趣,所以第二項與第一項強相關,第三項和第二項也是強相關。那是不是可以合併第一項和第二項呢?
3、 拿到一個樣本,特徵非常多,而樣例特別少,這樣用迴歸去直接擬合非常困難,容易過度擬合。比如北京的房價:假設房子的特徵是(大小、位置、朝向、是否學區房、建造年代、是否二手、層數、所在層數),搞了這麼多特徵,結果只有不到十個房子的樣例。要擬合房子特徵->房價的這麼多特徵,就會造成過度擬合。
4、 這個與第二個有點類似,假設在IR中我們建立的文件-詞項矩陣中,有兩個詞項為“learn”和“study”,在傳統的向量空間模型中,認為兩者獨立。然而從語義的角度來講,兩者是相似的,而且兩者出現頻率也類似,是不是可以合成為一個特徵呢?
5、 在訊號傳輸過程中,由於通道不是理想的,通道另一端收到的訊號會有噪音擾動,那麼怎麼濾去這些噪音呢?
回顧我們之前介紹的《模型選擇和規則化》,裡面談到的特徵選擇的問題。但在那篇中要剔除的特徵主要是和類標籤無關的特徵。比如“學生的名字”就和他的“成績”無關,使用的是互資訊的方法。
而這裡的特徵很多是和類標籤有關的,但裡面存在噪聲或者冗餘。在這種情況下,需要一種特徵降維的方法來減少特徵數,減少噪音和冗餘,減少過度擬合的可能性。
下面探討一種稱作主成分分析(PCA)的方法來解決部分上述問題。PCA的思想是將n維特徵對映到k維上(k<n),這k維是全新的正交特徵。這k維特徵稱為主元,是重新構造出來的k維特徵,而不是簡單地從n維特徵中去除其餘n-k維特徵。
2. PCA計算過程
首先介紹PCA的計算過程:
假設我們得到的2維資料如下:
行代表了樣例,列代表特徵,這裡有10個樣例,每個樣例兩個特徵。可以這樣認為,有10篇文件,x是10篇文件中“learn”出現的TF-IDF,y是10篇文件中“study”出現的TF-IDF。也可以認為有10輛汽車,x是千米/小時的速度,y是英里/小時的速度,等等。
第一步分別求x和y的平均值,然後對於所有的樣例,都減去對應的均值。這裡x的均值是1.81,y的均值是1.91,那麼一個樣例減去均值後即為(0.69,0.49),得到
第二步,求特徵協方差矩陣,如果資料是3維,那麼協方差矩陣是
這裡只有x和y,求解得
對角線上分別是x和y的方差,非對角線上是協方差。協方差大於0表示x和y若有一個增,另一個也增;小於0表示一個增,一個減;協方差為0時,兩者獨立。協方差絕對值越大,兩者對彼此的影響越大,反之越小。
第三步,求協方差的特徵值和特徵向量,得到
上面是兩個特徵值,下面是對應的特徵向量,特徵值0.0490833989對應特徵向量為![]() ,這裡的特徵向量都歸一化為單位向量。
,這裡的特徵向量都歸一化為單位向量。
第四步,將特徵值按照從大到小的順序排序,選擇其中最大的k個,然後將其對應的k個特徵向量分別作為列向量組成特徵向量矩陣。
這裡特徵值只有兩個,我們選擇其中最大的那個,這裡是1.28402771,對應的特徵向量是![]() 。
。
第五步,將樣本點投影到選取的特徵向量上。假設樣例數為m,特徵數為n,減去均值後的樣本矩陣為DataAdjust(m*n),協方差矩陣是n*n,選取的k個特徵向量組成的矩陣為EigenVectors(n*k)。那麼投影后的資料FinalData為
這裡是
FinalData(10*1) = DataAdjust(10*2矩陣)×特徵向量![]()
得到結果是
這樣,就將原始樣例的n維特徵變成了k維,這k維就是原始特徵在k維上的投影。
上面的資料可以認為是learn和study特徵融合為一個新的特徵叫做LS特徵,該特徵基本上代表了這兩個特徵。
上述過程有個圖描述:
正號表示預處理後的樣本點,斜著的兩條線就分別是正交的特徵向量(由於協方差矩陣是對稱的,因此其特徵向量正交),最後一步的矩陣乘法就是將原始樣本點分別往特徵向量對應的軸上做投影。
如果取的k=2,那麼結果是
這就是經過PCA處理後的樣本資料,水平軸(上面舉例為LS特徵)基本上可以代表全部樣本點。整個過程看起來就像將座標系做了旋轉,當然二維可以圖形化表示,高維就不行了。上面的如果k=1,那麼只會留下這裡的水平軸,軸上是所有點在該軸的投影。
這樣PCA的過程基本結束。在第一步減均值之後,其實應該還有一步對特徵做方差歸一化。比如一個特徵是汽車速度(0到100),一個是汽車的座位數(2到6),顯然第二個的方差比第一個小。因此,如果樣本特徵中存在這種情況,那麼在第一步之後,求每個特徵的標準差![]() ,然後對每個樣例在該特徵下的資料除以
,然後對每個樣例在該特徵下的資料除以![]() 。
。
歸納一下,使用我們之前熟悉的表示方法,在求協方差之前的步驟是:
其中![]() 是樣例,共m個,每個樣例n個特徵,也就是說
是樣例,共m個,每個樣例n個特徵,也就是說![]() 是n維向量。
是n維向量。![]() 是第i個樣例的第j個特徵。
是第i個樣例的第j個特徵。![]() 是樣例均值。
是樣例均值。![]() 是第j個特徵的標準差。
是第j個特徵的標準差。
整個PCA過程貌似及其簡單,就是求協方差的特徵值和特徵向量,然後做資料轉換。但是有沒有覺得很神奇,為什麼求協方差的特徵向量就是最理想的k維向量?其背後隱藏的意義是什麼?整個PCA的意義是什麼?
3. PCA理論基礎
要解釋為什麼協方差矩陣的特徵向量就是k維理想特徵,我看到的有三個理論:分別是最大方差理論、最小錯誤理論和座標軸相關度理論。這裡簡單探討前兩種,最後一種在討論PCA意義時簡單概述。
3.1 最大方差理論
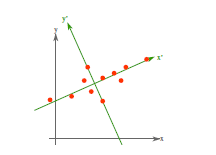
在訊號處理中認為訊號具有較大的方差,噪聲有較小的方差,信噪比就是訊號與噪聲的方差比,越大越好。如前面的圖,樣本在橫軸上的投影方差較大,在縱軸上的投影方差較小,那麼認為縱軸上的投影是由噪聲引起的。
因此我們認為,最好的k維特徵是將n維樣本點轉換為k維後,每一維上的樣本方差都很大。
比如下圖有5個樣本點:(已經做過預處理,均值為0,特徵方差歸一)
下面將樣本投影到某一維上,這裡用一條過原點的直線表示(前處理的過程實質是將原點移到樣本點的中心點)。
假設我們選擇兩條不同的直線做投影,那麼左右兩條中哪個好呢?根據我們之前的方差最大化理論,左邊的好,因為投影后的樣本點之間方差最大。
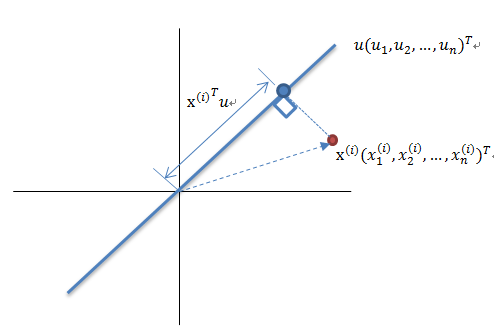
這裡先解釋一下投影的概念:
紅色點表示樣例![]() ,藍色點表示
,藍色點表示![]() 在u上的投影,u是直線的斜率也是直線的方向向量,而且是單位向量。藍色點是
在u上的投影,u是直線的斜率也是直線的方向向量,而且是單位向量。藍色點是![]() 在u上的投影點,離原點的距離是
在u上的投影點,離原點的距離是![]() (即
(即![]() 或者
或者![]() )由於這些樣本點(樣例)的每一維特徵均值都為0,因此投影到u上的樣本點(只有一個到原點的距離值)的均值仍然是0。
)由於這些樣本點(樣例)的每一維特徵均值都為0,因此投影到u上的樣本點(只有一個到原點的距離值)的均值仍然是0。
回到上面左右圖中的左圖,我們要求的是最佳的u,使得投影后的樣本點方差最大。
由於投影后均值為0,因此方差為:
中間那部分很熟悉啊,不就是樣本特徵的協方差矩陣麼(![]() 的均值為0,一般協方差矩陣都除以m-1,這裡用m)。
的均值為0,一般協方差矩陣都除以m-1,這裡用m)。
We got it!![]() 就是
就是![]() 的特徵值,u是特徵向量。最佳的投影直線是特徵值
的特徵值,u是特徵向量。最佳的投影直線是特徵值![]() 最大時對應的特徵向量,其次是
最大時對應的特徵向量,其次是![]() 第二大對應的特徵向量,依次類推。
第二大對應的特徵向量,依次類推。
因此,我們只需要對協方差矩陣進行特徵值分解,得到的前k大特徵值對應的特徵向量就是最佳的k維新特徵,而且這k維新特徵是正交的。得到前k個u以後,樣例![]() 通過以下變換可以得到新的樣本。
通過以下變換可以得到新的樣本。
通過選取最大的k個u,使得方差較小的特徵(如噪聲)被丟棄。
這是其中一種對PCA的解釋
3.2 最小平方誤差理論
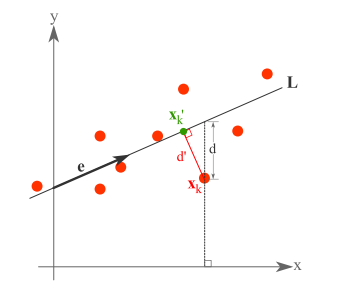
假設有這樣的二維樣本點(紅色點),回顧我們前面探討的是求一條直線,使得樣本點投影到直線上的點的方差最大。本質是求直線,那麼度量直線求的好不好,不僅僅只有方差最大化的方法。再回想我們最開始學習的線性迴歸等,目的也是求一個線性函式使得直線能夠最佳擬合樣本點,那麼我們能不能認為最佳的直線就是迴歸後的直線呢?迴歸時我們的最小二乘法度量的是樣本點到直線的座標軸距離。比如這個問題中,特徵是x,類標籤是y。迴歸時最小二乘法度量的是距離d。如果使用迴歸方法來度量最佳直線,那麼就是直接在原始樣本上做迴歸了,跟特徵選擇就沒什麼關係了。
因此,我們打算選用另外一種評價直線好壞的方法,使用點到直線的距離d’來度量。
現在有n個樣本點![]() ,每個樣本點為m維(這節內容中使用的符號與上面的不太一致,需要重新理解符號的意義)。將樣本點
,每個樣本點為m維(這節內容中使用的符號與上面的不太一致,需要重新理解符號的意義)。將樣本點![]() 在直線上的投影記為
在直線上的投影記為![]() ,那麼我們就是要最小化
,那麼我們就是要最小化
這個公式稱作最小平方誤差(Least Squared Error)。
而確定一條直線,一般只需要確定一個點,並且確定方向即可。
第一步確定點:
假設要在空間中找一點![]() 來代表這n個樣本點,“代表”這個詞不是量化的,因此要量化的話,我們就是要找一個m維的點
來代表這n個樣本點,“代表”這個詞不是量化的,因此要量化的話,我們就是要找一個m維的點![]() ,使得
,使得
最小。其中![]() 是平方錯誤評價函式(squared-error
criterion function),假設m為n個樣本點的均值:
是平方錯誤評價函式(squared-error
criterion function),假設m為n個樣本點的均值:
那麼平方錯誤可以寫作:
第二步確定方向:
我們從![]() 拉出要求的直線(這條直線要過點m),假設直線的方向是單位向量e。那麼直線上任意一點,比如
拉出要求的直線(這條直線要過點m),假設直線的方向是單位向量e。那麼直線上任意一點,比如![]() 就可以用點m和e來表示
就可以用點m和e來表示
我們重新定義最小平方誤差:
這裡的k只是相當於i。![]() 就是最小平方誤差函式,其中的未知引數是
就是最小平方誤差函式,其中的未知引數是![]() 和e。
和e。
這個結果意思是說,如果知道了e,那麼將![]() 與e做內積,就可以知道了
與e做內積,就可以知道了![]() 在e上的投影離m的長度距離,不過這個結果不用求都知道。
在e上的投影離m的長度距離,不過這個結果不用求都知道。
其中![]() 與協方差矩陣類似,只是缺少個分母n-1,我們稱之為雜湊矩陣(scatter matrix)。
與協方差矩陣類似,只是缺少個分母n-1,我們稱之為雜湊矩陣(scatter matrix)。
然後可以對e求偏導數,但是e需要首先滿足![]() ,引入拉格朗日乘子
,引入拉格朗日乘子![]() ,來使
,來使![]() 最大(
最大(![]() 最小),令
最小),令
求偏導
這裡存在對向量求導數的技巧,方法這裡不多做介紹。可以去看一些關於矩陣微積分的資料,這裡求導時可以將![]() 看作是
看作是![]() ,將
,將![]() 看做是
看做是![]() 。
。
導數等於0時,得
兩邊除以n-1就變成了,對協方差矩陣求特徵值向量了。
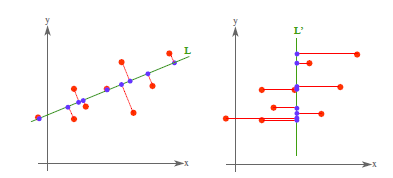
從不同的思路出發,最後得到同一個結果,對協方差矩陣求特徵向量,求得後特徵向量上就成為了新的座標,如下圖:
這時候點都聚集在新的座標軸周圍,因為我們使用的最小平方誤差的意義就在此。
4. PCA理論意義
PCA將n個特徵降維到k個,可以用來進行資料壓縮,如果100維的向量最後可以用10維來表示,那麼壓縮率為90%。同樣影象處理領域的KL變換使用PCA做影象壓縮。但PCA要保證降維後,還要保證資料的特性損失最小。再看回顧一下PCA的效果。經過PCA處理後,二維資料投影到一維上可以有以下幾種情況:
我們認為左圖好,一方面是投影后方差最大,一方面是點到直線的距離平方和最小,而且直線過樣本點的中心點。為什麼右邊的投影效果比較差?直覺是因為座標軸之間相關,以至於去掉一個座標軸,就會使得座標點無法被單獨一個座標軸確定。
PCA得到的k個座標軸實際上是k個特徵向量,由於協方差矩陣對稱,因此k個特徵向量正交。看下面的計算過程。
假設我們還是用![]() 來表示樣例,m個樣例,n個特徵。特徵向量為e,
來表示樣例,m個樣例,n個特徵。特徵向量為e,![]() 表示第i個特徵向量的第1維。那麼原始樣本特徵方程可以用下面式子來表示:
表示第i個特徵向量的第1維。那麼原始樣本特徵方程可以用下面式子來表示:
前面兩個矩陣乘積就是協方差矩陣![]() (除以m後),原始的樣本矩陣A是第二個矩陣m*n。
(除以m後),原始的樣本矩陣A是第二個矩陣m*n。
我們最後得到的投影結果是![]() ,E是k個特徵向量組成的矩陣,展開如下:
,E是k個特徵向量組成的矩陣,展開如下:
得到的新的樣例矩陣就是m個樣例到k個特徵向量的投影,也是這k個特徵向量的線性組合。e之間是正交的。從矩陣乘法中可以看出,PCA所做的變換是將原始樣本點(n維),投影到k個正交的座標系中去,丟棄其他維度的資訊。舉個例子,假設宇宙是n維的(霍金說是11維的),我們得到銀河系中每個星星的座標(相對於銀河系中心的n維向量),然而我們想用二維座標去逼近這些樣本點,假設算出來的協方差矩陣的特徵向量分別是圖中的水平和豎直方向,那麼我們建議以銀河系中心為原點的x和y座標軸,所有的星星都投影到x和y上,得到下面的圖片。然而我們丟棄了每個星星離我們的遠近距離等資訊。
這裡,我們討論特徵選擇和特徵提取,前者選取重要的特徵子集,後者由原始輸入形成較少的新特徵,理想情況下,無論是分類還是迴歸,我們不應該將特徵選擇或特徵提取作為一個單獨的程序,分類或者回歸方法應該能夠利用任何必要的特徵,而丟棄不相關的特徵。但是,考慮到演算法儲存量和時間的複雜
因為專案需要,研究基於機器學習的人工智慧。
俗話說,工欲善其事,必先利其器。
學習人工智慧,首先就要有一個開發環境,也就是寫程式碼跑模擬的地方。
折騰了幾天,終於成功建立了基於tensorflow和keras的開發環境。
中間遇到了許多問題,在同事及網路
二叉堆(Binary Heap)
(1)structure property
Heap(堆)是一個除了底層節點外的完全填滿的二叉樹,底層可以不完全,左到右填充節點。(a heap is a binar 一、命令介紹
useradd 用於建立新的使用者
usermod 用於修改使用者屬性
userdel 用於刪除使用者
--------------------
零基礎學習hadoop,沒有想象的那麼困難,也沒有想象的那麼容易。在剛接觸雲端計算,曾經想過培訓,但是培訓機構的選擇就讓我很糾結。所以索性就自己學習了。整個過程整理一下,給大家參考,歡迎討論,共同學習。
從一開始什麼都不懂,到能夠搭建叢集,開發。整個過程,只要有Linux基礎,虛擬機器化和java基礎,其
原文地址
附帶連結(待看)
中級篇學習筆記
進度:內容很多很雜,先看一下後半部分的hadoop生態系統。
操作:並未實際操作。
hadoop生態系統
最常用的是hive和hbase,因此著重學習這兩個。
hive相關學習
one 這一 調用 現實生活 ram 每次 open java 自我
面向過程:根據業務邏輯從上到下寫壘代碼
函數式:將某功能代碼封裝到函數中,日後便無需重復編寫,僅調用函數即可
面向對象:對函數進行分類和封裝,讓開發“更快更好更強...”
面向過程編程最易被初學者接受
轉載原文:https://mp.weixin.qq.com/s/TQvmt84imz77oTcH7KQ1rQ
寫過java的都知道:所有的物件都必須建立;或者說:使用物件之前必須先建立。而使用ioc之後,你就可以不再手動建立物件,而是從ioc容器中直接獲取物件。
就好像我們
原文轉載:https://mp.weixin.qq.com/s/6WK2oV-vaqPGQpIIR5UeHA
什麼是aop
AOP(Aspect-OrientedProgramming,面向方面程式設計),可以說是OOP(Object-Oriented Programing,面向物件程式設計
原文轉載:https://mp.weixin.qq.com/s/z0fBCVkN7F1zIfBDzpVTsA
關於快取
快取是實際工作中非常常用的一種提高效能的方法。而在java中,所謂快取,就是將程式或系統經常要呼叫的物件存在記憶體中,再次呼叫時可以快速從記憶體中獲取物件,不必再去建立新的
轉載原文:https://mp.weixin.qq.com/s/1G5CVoEmgioDkZfnAapoTw
Spring MVC簡介與執行原理
Spring的模型-檢視-控制器(MVC)框架是圍繞一個DispatcherServlet來設計的,這個Servlet會把請求分發給各個處理器,並 nat原理 分享課 多出口 spf 鏈接 baidu 路徑 .com 體系 Yeslab 華為安全HCIE七門之-防火墻基礎(12篇)
Yeslab 全套華為安全HCIE七門之第二門防火墻基礎(12篇),第一門課論壇很早就有了,可自行下載,後面的陸續分享給大家。
華為安全H
俗話說:無規矩不成方圓,做事做人都一樣。寫程式碼也是一樣,都需要遵循基本的程式碼規範和格式。只有瞭解和遵循規則,才能寫出更高質量的程式碼,才能在錯綜複雜的 Bug 中快速定位出問題並找到解決方案。相信大家在《Python 單元測試框架之 Pytest 剖解入門(第一篇)》 已
前言
在向網頁進行了提交請求之類的之後,我們可以得到了網頁的返回內容,裡面自然而然會有我們想要的資料,但是html元素文字這麼多,我們不可能一 一去找我們需要的資料,這時就需要用到正則表示式了,正則表示式是學爬蟲必須學的內容,而且不止python可以用,jav 本篇文章主要從mapreduce執行作業的過程,shuffle,以及mapreduce作業失敗的容錯幾個方面進行詳解。
一、mapreduce作業執行過程
1.1、mapreduce介紹
MapReduce是一種程式設計模型,用於大規模資料集(大於1TB)的並行運 一、概述
優化前我們需要知道hadoop適合幹什麼活,適合什麼場景,在工作中,我們要知道業務是怎樣的,能才結合平臺資源達到最有優化。除了這些我們當然還要知道mapreduce的執行過程,比如從檔案的讀取,map處理,shuffle過程,reduce處理,檔案的輸出或者
這裡,我們討論特徵選擇和特徵提取,前者選取重要的特徵子集,後者由原始輸入形成較少的新特徵,理想情況下,無論是分類還是迴歸,我們不應該將特徵選擇或特徵提取作為一個單獨的程序,分類或者回歸方法應該能夠利用任何必要的特徵,而丟棄不相關的特徵。但是,考慮到演算法儲存量和時間的複雜度,
原文連結:http://blog.csdn.net/heyongluoyao8/article/details/49408131
在分類中如何處理訓練集中不平衡問題
在很多機器學習任務中,訓練集中可能會存在某個或某些類別下的樣本數遠大於另一些類別下的樣本數目。即類別不平衡,為了使得學習達
轉自:https://www.cnblogs.com/lianyingteng/p/7792693.html
在機器學習問題中,我們通過訓練資料集學習得到的其實就是一組模型的引數,然後通過學習得到的引數確定模型的表示,最後用這個模型再去進行我們後續的預測分類等工作。在模型訓練過程中,我們會對訓練
轉自:https://blog.csdn.net/bryan__/article/details/52026214 其實這篇文章真正出處來自:csuldw
本文主要回顧下幾個常用演算法的適應場景及其優缺點!
機器學習演算法太多了,分類、迴歸、聚類、推薦、影象識別領域等等,要想找到一個合適演算 相關推薦
系統學習機器學習之維度歸約(完整篇)
基於python的機器學習人工智慧入門之tensorflow / keras安裝(Windows環境)
Ted 帶你學習資料結構 之 二叉堆(Binary Heap)
Linux學習歷程——Centos 7 賬戶管理命令(使用者篇)useradd usermod userdel
大資料-零基礎學習hadoop到上手工作線路指導(初級篇)
2016.6.13 零基礎學習hadoop到上手工作線路指導(中級篇)
Python之面向對象(初級篇)
Spring之思維導圖(IOC篇)
Spring之思維導圖(AOP篇)
Spring之思維導圖(Cache篇)
Spring之思維導圖(MVC篇)
Yeslab 華為安全HCIE七門之-防火墻基礎(12篇)
Python+Pytest 單元測試框架之執行用例(第二篇)
python之正則表示式(基礎篇)
hadoop之mapreduce詳解(基礎篇)
hadoop之mapreduce詳解(優化篇)
系統學習機器學習之特徵工程(一)--維度歸約
系統學習機器學習之樣本不平衡問題處理
系統學習機器學習之特徵工程(二)--離散型特徵編碼方式:LabelEncoder、one-hot與啞變數*
系統學習機器學習之總結(二)--機器學習演算法比較

![clip_image001[4] clip_image001[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110403541.png)
![clip_image002[4] clip_image002[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110405460.png)
![clip_image003[4] clip_image003[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110402603.png)
![clip_image004[4] clip_image004[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110418982.png)
![clip_image005[4] clip_image005[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110418949.png)
![clip_image012[4] clip_image012[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110423800.png)
![clip_image013[4] clip_image013[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110441716.png)
![clip_image014[4] clip_image014[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110452456.png)
![clip_image017[4] clip_image017[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110471909.png)
![clip_image026[4] clip_image026[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110513465.png)
![clip_image028[4] clip_image028[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/20110418211051367.jpg)
![clip_image042[4] clip_image042[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110578868.png)
![clip_image059[4] clip_image059[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182111061880.png)