BP（Back Propagation）網路是1986年由Rumelhart和McCelland為首的科學家小組提出，是一種按誤差逆傳播演算法訓練的多層前饋網路，是目前應用最廣泛的之一。BP網路能學習和存貯大量的輸入-輸出模式對映關係，而無需事前揭示描述這種對映關係的數學方程。它的學習規則是使用最速下降法，通過反向傳播來不斷調整網路的權值和閾值，使網路的誤差平方和最小。模型拓撲結構包括輸入層（input）、隱層(hide layer)和輸出層(output layer)。

1 傳統的BP演算法簡述

BP演算法是一種有監督式的學習演算法，其主要思想是：輸入學習樣本，使用反向傳播演算法對網路的權值和偏差進行反覆的調整訓練，使輸出的向量與期望向量儘可能地接近，當網路輸出層的誤差平方和小於指定的誤差時訓練完成，儲存網路的權值和偏差。具體步驟如下：

　　（1）初始化，隨機給定各連線權及閥值。

　　（2）由給定的輸入輸出模式對計算隱層、輸出層各單元輸出　　

　　（3）計算新的連線權及閥值，計算公式如下：

　　（4）選取下一個輸入模式對返回第2步反覆訓練直到網路設輸出誤差達到要求結束訓練。

　　傳統的BP演算法，實質上是把一組樣本輸入/輸出問題轉化為一個非線性優化問題，並通過負，利用迭代運算求解權值問題的一種學習方法，但其收斂速度慢且容易陷入區域性極小，為此提出了一種新的演算法，即高斯消元法。

2 改進的BP網路演算法

2．1 改進演算法概述

　　此前有人提出：任意選定一組自由權，通過對傳遞函式建立線性方程組，解得待求權。本文在此基礎上將給定的目標輸出直接作為線性方程等式代數和來建立線性方程組，不再通過對傳遞函式求逆來計算神經元的淨輸出，簡化了運算步驟。沒有采用誤差反饋原理，因此用此法訓練出來的神經網路結果與傳統演算法是等效的。其基本思想是：由所給的輸入、輸出模式對通過作用於神經網路來建立線性方程組，運用高斯消元法解線性方程組來求得未知權值，而未採用傳統

2．2 改進演算法的具體步驟

　　對給定的樣本模式對，隨機選定一組自由權，作為輸出層和隱含層之間固定權值，通過傳遞函式計算隱層的實際輸出，再將輸出層與隱層間的權值作為待求量，直接將目標輸出作為等式的右邊建立方程組來求解。

　　（1）隨機給定隱層和輸入層間神經元的初始權值。

　　（2）由給定的樣本輸入計算出隱層的實際輸出。

　　（3）計算輸出層與隱層間的權值。以輸出層的第r個神經元為物件，由給定的輸出目標值作為等式的多項式值建立方程。　

（4）重複第三步就可以求出輸出層m個神經元的權值，以求的輸出層的權矩陣加上隨機固定的隱層與輸入層的權值就等於神經網路最後訓練的權矩陣。

3 計算機運算例項

 %% 清空環境變數
clc
clear

%% 訓練資料預測資料
data=importdata('test.txt');

%從1到768間隨機排序
k=rand(1,768);
[m,n]=sort(k);

%輸入輸出資料
input=data(:,1:8);
output =data(:,9);

%隨機提取500個樣本為訓練樣本，268個樣本為預測樣本
input_train=input(n(1:500),:)';
output_train=output(n(1:500),:)';
input_test=input(n(501:768),:)';
output_test=output(n(501:768),:)';

%輸入資料歸一化
[inputn,inputps]=mapminmax(input_train);

%% BP網路訓練
% %初始化網路結構
net=newff(inputn,output_train,10);

net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0000004;

%% 網路訓練
net=train(net,inputn,output_train);

%% BP網路預測
%預測資料歸一化
inputn_test=mapminmax('apply',input_test,inputps);
 
%網路預測輸出
BPoutput=sim(net,inputn_test);

%% 結果分析
%根據網路輸出找出資料屬於哪類
BPoutput(find(BPoutput<0.5))=0;
BPoutput(find(BPoutput>=0.5))=1;

%% 結果分析
%畫出預測種類和實際種類的分類圖
figure(1)
plot(BPoutput,'og')
hold on
plot(output_test,'r*');
legend('預測類別','輸出類別')
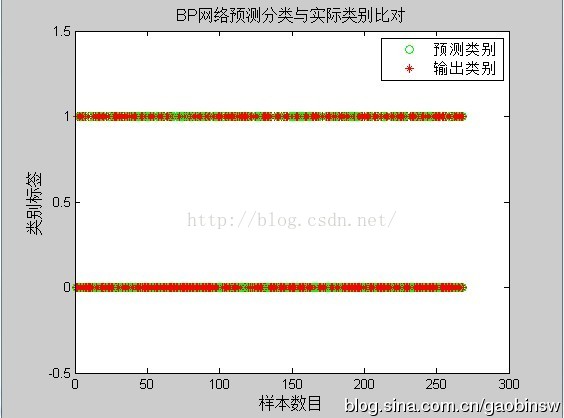
title('BP網路預測分類與實際類別比對','fontsize',12)
ylabel('類別標籤','fontsize',12)
xlabel('樣本數目','fontsize',12)
ylim([-0.5 1.5])

%預測正確率
rightnumber=0;
for i=1:size(output_test,2)
    if BPoutput(i)==output_test(i)
        rightnumber=rightnumber+1;
    end
end
rightratio=rightnumber/size(output_test,2)*100;

sprintf('測試準確率=%0.2f',rightratio)