CORDIC也許是最值得研究的硬體實現技術了，但是卻又很難被實現：它的優勢就是同樣的硬體可以被實現為多種函式，但是效能卻非常不好。High-order polynomial approximation可以給予很低的誤差實現，但是這普遍不適合硬體實現。一種很有成效的方法是table-driven方法，但是如果表很大將會帶來很大的開銷。

對於大多數函式，通過均勻分隔來進行插值不夠理想的。在sigmoid函式這個例子中，顯然更多的間隔應該被使用。然而硬體實現需要更快的將引數對映到合適的間隔上。本著這種選擇和線性插值法，最關鍵的就在於函式值和每個間隔如何聯絡起來。最普遍的方法就是武斷的選擇間隔的重點，也就是如果x∈[L,U]，f(x)=f(L/2 + U/2)，或者去選擇一個值來減小這種絕對誤差。這並不是一種好的方法。對於一個定點間隔，最好的函式值一般並不是中點所對應的。這取決於函式的“curvature(曲率)”，相對誤差可能比絕對誤差更重要。例如對於sigmoid函式，f(x) =1/(1+e^-x)，函式是關於原點對稱的，但是相對誤差只在一面變得更加明顯，兩邊的誤差取決於間隔，因此絕對誤差並不總是一個常量或者是線性的。

         普遍的方法是：假設I = [L,U]做為一個間隔，L<U 且f : I ->R被逼近，假設f’ :I->R是一個線性函式，f’(x) = c1+c2x，對於常量c1和c2，對於f，我們的目標是觀察相對誤差函式。

下面是利用Matlab對分段插值來逼近sigmoid函式的程式碼：

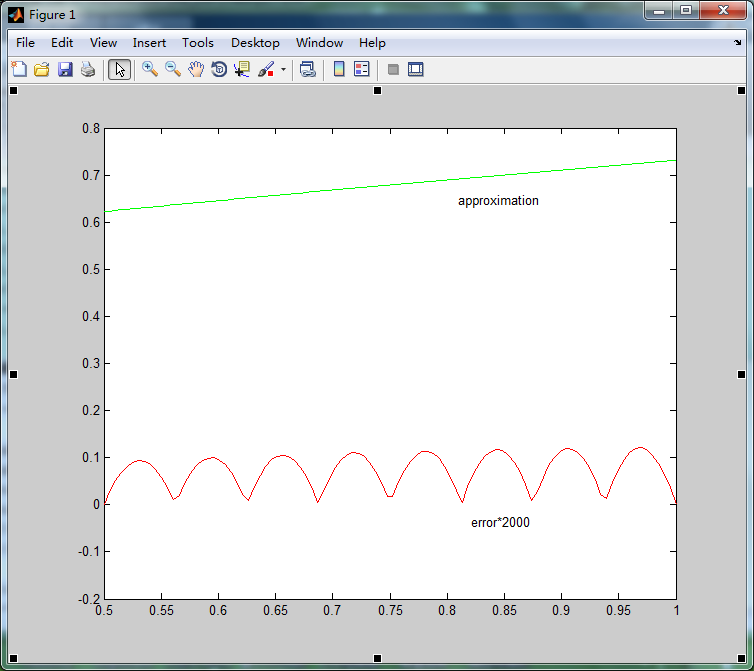
%% 插值誤差計算
t = 0.5:1/16:1; %9個
for i = 1:8
    i
    sigL(i) = 1/(1 + exp(-t(i)));
    sigU(i) = 1/(1 + exp(-t(i+1)));
    %sigL(i)
    %sigU(i)
    c2(i) = (sigU(i)-sigL(i))/(t(i+1)-t(i));
    c1(i) = sigU(i)-c2(i)*t(i+1);
end
f2 = (c1(1)+c2(1)*x).*(x>=t(1)&x<t(2))+(c1(2)+c2(2)*x).*(x>=t(2)&x<t(3))+(c1(3)+c2(3)*x).*(x>=t(3)&x<t(4))+...
    (c1(4)+c2(4)*x).*(x>=t(4)&x<t(5))+(c1(5)+c2(5)*x).*(x>=t(5)&x<t(6))+(c1(6)+c2(6)*x).*(x>=t(6)&x<t(7))+...
    (c1(7)+c2(7)*x).*(x>=t(7)&x<t(8))+(c1(8)+c2(8)*x).*(x>=t(8)&x<=t(9));
f1 = 1./(1+exp(-x)).*(x>=0.5 & x <=1);
%x = linspace(0.5,1);

figure(1)
plot(x,f2,'g'); %分段函式繪圖
wucha = (f1-f2)./f1*2000;
hold on;
plot(x,wucha,'r');
axis([0.5,1,-0.2,0.8]);
 

下面是模擬圖