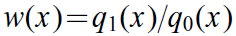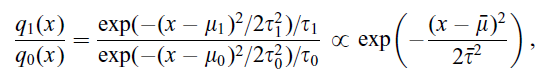tensorflow ————batchnorm原理及程式碼詳解
Batchnorm————深度學習中常用到的加速神經網路訓練,加速收斂及穩定性的演算法。
1.batchnorm主要解決的問題(BN的歸一化手段很好用)
batchnorm直譯過來就是批規範化,就是為了解決分佈變化問題。
深度學習上都要對資料做歸一化處理,因為深度神經網路主要就是為了學習訓練資料的分佈,並在測試集上達到很好的泛化效果。
但是我們每一個batch輸入的資料都具有不同的分佈,顯然會給網路的訓練帶來困難。另一方面,資料經過一層層網路計算之後,其資料分佈也在發生變化,此現象稱為Internal Covariate Shift。
什麼是Covariate shift
假設x是屬於特徵空間的某一樣本點,y是標籤。covariate這個詞,其實指這裡的x,那麼covariate shift可以直譯為:樣本點x的變化。
規範一點講:
假設q1(x)是測試集中的一個樣本點的概率密度,q0(x)是訓練集中的一個樣本概率密度。最終我們估計一個條件概率密度p(y|x,θ),它是由x和一組引數θ={θ1,θ2......θm}所決定。對於一組引數來說,對應loss(θ)函式評估效能的好壞。
綜上,當我們找出在q0(x)分佈上最優的一組θ'時,能否保證q1(x)上測試時也最好呢?
傳統機器學習假設訓練集和測試集是獨立同分布的,即q0(x)=q1(x),所以可以推出最優θ'依然可以保證q1(x)最優。但現實當中這個假設往往不成立,伴隨新資料產生,老資料會過時,當q0(x)不再等於q1(x)時,就被稱作covariate shift
怎麼解決covariate shift??
以上已經知道一個樣本點分別在訓練集和測試集上的概率密度q0(x)和q1(x),實際當中的解決方案是附加一個由x決定的權值
使得在訓練過程當中對於q1(x)很大或者q0(x)很小的樣本視作“重要”樣本,這樣的樣本是有益於測試集預測的,我們應該儘量把它分類正確。而對於q1(x)很小或者q0(x)很大的樣本,它只是被時代遺棄的“老資料”,這些樣本對於模型訓練的意義也是無關緊要了
舉個例子:
現在我們要通過多項式迴歸預測某一個函式。資料產生通過下式,並且用正態分佈產生噪聲加在上面
通過一個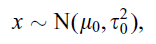
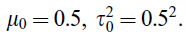
假設模型的形式是
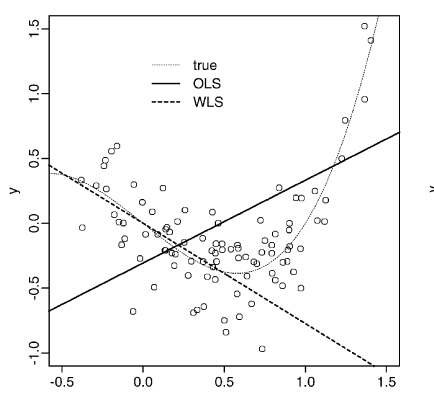
實驗結果如左圖,最終得到一條線,對應圖中OLS
根據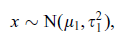
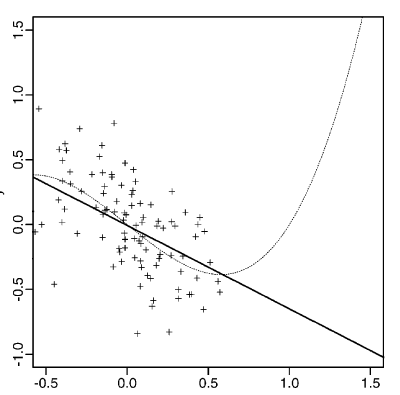
最理想的情況,我們直接擬合測試集的點,得到右圖中的實線,和左邊的線完全不一樣,看出covariate shift發生了。
但是我們需要測試集的輔助來解決covariate shift問題(如果直接訓練測試集就毫無意義了),求得
通過附加權值的方法,最終訓練得到左圖中虛線WLS
可以看出最終得到的模型,是可以很好的適應測試集的。
從遷移學習的角度看,這也是一種用source domain的標籤資料,結合target domain的無標籤資料,指導進行知識的遷移的方法。
第二節 batchnorm原理
顧名思義,batch normalization嘛,就是“批規範化”咯。Google在ICML文中描述的非常清晰,即在每次SGD時,通過mini-batch來對相應的activation做規範化操作,使得結果(輸出訊號各個維度)的均值為0,方差為1. 而最後的“scale and shift”操作則是為了讓因訓練所需而“刻意”加入的BN能夠有可能還原最初的輸入(即當之前就說過,為了減小Internal covariate shift,對神經網路的每一層做歸一化不就可以了,假設將每一層輸出後的資料都歸一化到0均值,1方差,滿足正太分佈,但是,此時有一個問題,每一層的資料分佈都是標準正太分佈,導致其完全學習不到輸入資料的特徵,因為,費勁心思學習到的特徵分佈被歸一化了,因此,直接對每一層做歸一化顯然是不合理的。
但是如果稍作修改,加入可訓練的引數做歸一化,那就是BatchNorm 實現的了,接下來結合下圖的虛擬碼做詳細的分析:

關於DNN中的normalization,大家都知道白化(whitening),只是在模型訓練過程中進行白化操作會帶來過高的計算代價和運算時間。因此本文提出兩種簡化方式:1)直接對輸入訊號的每個維度做規範化(“normalize each scalar feature independently”);2)在每個mini-batch中計算得到mini-batch mean和variance來替代整體訓練集的mean和variance. 這便是Algorithm 1.
作者:魏秀參
連結:https://www.zhihu.com/question/38102762/answer/85238569
來源:知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權,非商業轉載請註明出處。
之所以稱之為batchnorm是因為所norm的資料是一個batch的,假設輸入資料是β=x 1...m 共m個數據,輸出是y i =BN(x)
batchnorm 的步驟如下:
1.先求出此次批量資料x x的均值,μ β =1m∑ m i=1 x i
2.求出此次batch的方差,σ 2 β =1m∑ i=1 m(x i −μ β ) 2
3.接下來就是對x 做歸一化,得到x − i
4.最重要的一步,引入縮放和平移變數γ和β ,計算歸一化後的值,y i =γx − i +β
y i =γx − i
接下來詳細介紹一下這額外的兩個引數,之前也說過如果直接做歸一化不做其他處理,神經網路是學不到任何東西的,但是加入這兩個引數後,事情就不一樣了,先考慮特殊情況下,如果γ和β分別等於此batch的方差和均值,那麼y i yi不就還原到歸一化前的x 了嗎,也即是縮放平移到了歸一化前的分佈,相當於batchnorm 沒有起作用,β 和γ分別稱之為 平移引數和縮放參數 。這樣就保證了每一次資料經過歸一化後還保留的有學習來的特徵,同時又能完成歸一化這個操作,加速訓練。
先用一個簡單的程式碼舉個小栗子:
def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x : 輸入資料,設shape(B,L)
param:gama : 縮放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些引數
eps : 接近0的數,防止分母出現0
momentum : 動量引數,一般為0.9, 0.99, 0.999
running_mean :滑動平均的方式計算新的均值,訓練時計算,為測試資料做準備
running_var : 滑動平均的方式計算新的方差,訓練時計算,為測試資料做準備
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一個新的變數
x_mean=x.mean(axis=0) # 計算x的均值
x_var=x.var(axis=0) # 計算方差
x_normalized=(x-x_mean)/np.sqrt(x_var+eps) # 歸一化
results = gamma * x_normalized + beta # 縮放平移
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
#記錄新的值
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return results , bn_param- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
看完這個程式碼是不是對batchnorm有了一個清晰的理解,首先計算均值和方差,然後歸一化,然後縮放和平移,完事!但是這是在訓練中完成的任務,每次訓練給一個批量,然後計算批量的均值方差,但是在測試的時候可不是這樣,測試的時候每次只輸入一張圖片,這怎麼計算批量的均值和方差,於是,就有了程式碼中下面兩行,在訓練的時候實現計算好mean mean var var測試的時候直接拿來用就可以了,不用計算均值和方差。
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var- 1
- 2
所以,測試的時候是這樣的:
def Batchnorm_simple_for_test(x, gamma, beta, bn_param):
"""
param:x : 輸入資料,設shape(B,L)
param:gama : 縮放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些引數
eps : 接近0的數,防止分母出現0
momentum : 動量引數,一般為0.9, 0.99, 0.999
running_mean :滑動平均的方式計算新的均值,訓練時計算,為測試資料做準備
running_var : 滑動平均的方式計算新的方差,訓練時計算,為測試資料做準備
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一個新的變數
x_normalized=(x-running_mean )/np.sqrt(running_var +eps) # 歸一化
results = gamma * x_normalized + beta # 縮放平移
return results , bn_param- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
你是否理解了呢?如果還沒有理解的話,歡迎再多看幾遍。
第三節:Batchnorm原始碼解讀
本節主要講解一段tensorflow中Batchnorm Batchnorm的可以使用的程式碼3 3,如下:
程式碼來自知乎,這裡加入註釋幫助閱讀。
def batch_norm_layer(x, train_phase, scope_bn):
with tf.variable_scope(scope_bn):
# 新建兩個變數,平移、縮放因子
beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta', trainable=True)
gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma', trainable=True)
# 計算此次批量的均值和方差
axises = np.arange(len(x.shape) - 1)
batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')
# 滑動平均做衰減
ema = tf.train.ExponentialMovingAverage(decay=0.5)
def mean_var_with_update():
ema_apply_op = ema.apply([batch_mean, batch_var])
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean), tf.identity(batch_var)
# train_phase 訓練還是測試的flag
# 訓練階段計算runing_mean和runing_var,使用mean_var_with_update()函式
# 測試的時候直接把之前計算的拿去用 ema.average(batch_mean)
mean, var = tf.cond(train_phase, mean_var_with_update,
lambda: (ema.average(batch_mean), ema.average(batch_var)))
normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
return normed- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
至於此行程式碼tf.nn.batch_normalization()就是簡單的計算batchnorm過程啦,程式碼如下:
這個函式所實現的功能就如此公式:γ(x−μ)σ+β γ(x−μ)σ+β
def batch_normalization(x,
mean,
variance,
offset,
scale,
variance_epsilon,
name=None):
with ops.name_scope(name, "batchnorm", [x, mean, variance, scale, offset]):
inv = math_ops.rsqrt(variance + variance_epsilon)
if scale is not None:
inv *= scale
return x * inv + (offset - mean * inv
if offset is not None else -mean * inv)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
第四節:Batchnorm的優點
主要部分說完了,接下來對BatchNorm做一個總結:
- 沒有它之前,需要小心的調整學習率和權重初始化,但是有了BN可以放心的使用大學習率,但是使用了BN,就不用小心的調參了,較大的學習率極大的提高了學習速度,
- Batchnorm本身上也是一種正則的方式,可以代替其他正則方式如dropout等
- 另外,個人認為,batchnorm降低了資料之間的絕對差異,有一個去相關的性質,更多的考慮相對差異性,因此在分類任務上具有更好的效果。
注:或許大家都知道了,韓國團隊在2017NTIRE影象超解析度中取得了top1的成績,主要原因竟是去掉了網路中的batchnorm層,由此可見,BN並不是適用於所有任務的,在image-to-image這樣的任務中,尤其是超解析度上,影象的絕對差異顯得尤為重要,所以batchnorm的scale並不適合。
那BN到底是什麼原理呢?說到底還是為了防止“梯度彌散”。關於梯度彌散,大家都知道一個簡單的栗子:。在BN中,是通過將activation規範為均值和方差一致的手段使得原本會減小的activation的scale變大。可以說是一種更有效的local response normalization方法(見4.2.1節)。
5. When to use BN?
OK,說完BN的優勢,自然可以知道什麼時候用BN比較好。例如,在神經網路訓練時遇到收斂速度很慢,或梯度爆炸等無法訓練的狀況時可以嘗試BN來解決。另外,在一般使用情況下也可以加入BN來加快訓練速度,提高模型精度。