Problem

Reference

Meaning

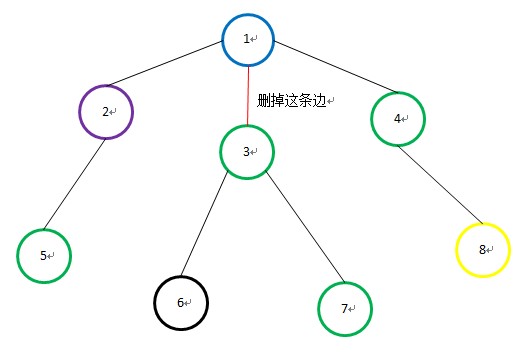
一棵 n 個結點的樹，每個結點都有一種顏色，問對與樹上的每條邊，刪掉它之後得到的兩棵樹中，共有的顏色有多少種（在那兩棵樹中都有的顏色就是公有的顏色）

Analysis

首先規定 1 號結點為整棵樹的根（其它號也可以）。

對與每一條邊，就看成是某個結點於它的父結點的連邊，於是，刪掉這條邊後兩個連同塊的共有顏色數，就等價於以這個結點為根的子樹裡共有顏色數（只有兩個連通塊，其中一個連通塊的“公共顏色”即是兩個連同塊的公共顏色）。

公共顏色是什麼呢？假如在其中一個連通塊中有 2 個綠色結點，而原樹一共有 4 個結點是綠色的，那綠色就是這兩個連通塊的公共顏色之一；反之，這個連通塊有一個黑色結點，而原樹也總共只有一個黑色結點，那黑色就是這個連通塊“私有”的顏色。

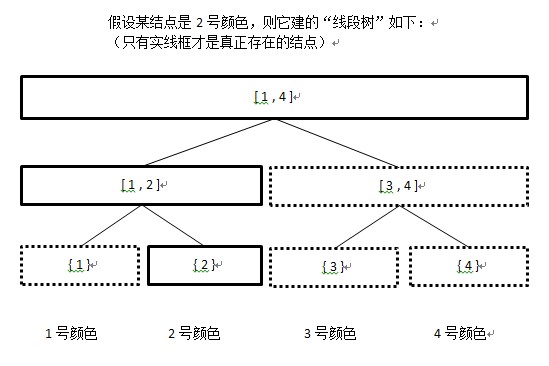
怎麼統計一棵子樹裡的共有顏色數呢？可以用線段樹。先不考慮空間，對每個結點都建一棵線段樹，記錄共有顏色數，然後將所有子結點的樹合併到父結點的樹裡，就得到了父結點的答案。但這麼做空間太大。

但其實對每個結點都沒必要真的建一整棵樹，因為根結點只有一種顏色，只需要一條鏈，而子樹的資訊，可以重用子樹建出來的結點，這樣就可以開得下。

具體看程式碼理解吧，線段樹新姿勢啊。

PS：我自己再補充一下吧，感覺這個建樹和結構已經與主席樹非常的像了。

Code

#include <cstdio> #include <cstring> using namespace std; const int N = 100000; struct edge { int to, nxt; } e[N<<1]; struct node { int lc, rc; // 左、右子結點的位置 int com; // 這棵樹中共有顏色的數量 int num; // 對葉子有用，表示這棵樹中這種顏色的結點數 } tree[18*N]; // 存樹結點的空間 int sz; // 樹結點總數 int c[N+1]; // 結點i的顏色 int sum[N+1]; // 顏色i的總數 int head[N+1]; // 前向星鏈頭 int root[N+1]; // 為第i個結點建的線段樹的根所在位置 int ans[N]; // 答案陣列 void add_edge(int f, int t, int id) { e[id].to = t; e[id].nxt = head[f]; head[f] = id; } inline void pushup(int x) { /* 不是葉子的結點，只需記錄共有顏色的數量 */ tree[x].com = tree[tree[x].lc].com + tree[tree[x].rc].com; } int build(int c, int l, int r) { int rt = ++sz; tree[rt].lc = tree[rt].rc = tree[rt].num = 0; if(l == r) { tree[rt].num = 1; tree[rt].com = tree[rt].num < sum[c]; } else { int m = l + r >> 1; /* 不需要建整棵樹，只要建一條鏈 */ if(c > m) tree[rt].rc = build(c, m+1, r); else tree[rt].lc = build(c, l, m); pushup(rt); } return rt; } void merge(int &fa, int ch, int l, int r) { if(!fa || !ch) { /* 若父結點那棵線段樹的這個結點為空， * 就直接重用子結點的線段樹的這條鏈 */ if(!fa) fa = ch; return; } if(l != r) { int m = l + r >> 1; merge(tree[fa].lc, tree[ch].lc, l, m); merge(tree[fa].rc, tree[ch].rc, m+1, r); pushup(fa); } else { /* 將子樹裡這種顏色的結點數加到父結點的樹 */ tree[fa].num += tree[ch].num; /* 這種顏色的結點不全在這棵樹中， * 則這種顏色是共有顏色 */ tree[fa].com = tree[fa].num < sum[l]; } } void dfs(int rt, int fa, int eid, int n) { /* 先給根結點“建棵樹” */ root[rt] = build(c[rt], 1, n); for(int i=head[rt]; ~i; i=e[i].nxt) { if(e[i].to == fa) continue; /* 先遞迴處理子結點 */ dfs(e[i].to, rt, i, n); /* 然後將子結點資訊合併上來 */ merge(root[rt], root[e[i].to], 1, n); } /* 加邊時同一條邊加了兩次， * 這個對映找出此邊在輸入時的序號 */ if(rt != 1) ans[eid/2+1] = tree[root[rt]].com; } int main() { tree[0].lc = tree[0].rc = tree[0].com = tree[0].num = 0; int n; while(~scanf("%d", &n)) { memset(sum, 0, sizeof sum); for(int i=1; i<=n; ++i) { scanf("%d", c+i); ++sum[c[i]]; } memset(head, -1, sizeof head); for(int i=1, a, b, id=0; i<n; ++i) { scanf("%d%d", &a, &b); add_edge(a, b, id++); add_edge(b, a, id++); } sz = 0; memset(root, 0, sizeof root); dfs(1, 0, 0, n); for(int i=1; i<n; ++i) printf("%d\n", ans[i]); } return 0; }