迷宮是許多小方格構成的矩形，在每個小方格中有的是牆（用1表示），有的是路（用0表示）。走迷宮就是從一個小方格沿上、下、左、右四個方向到鄰近的方格，當然不能穿牆。設迷宮的入口是在左上角（1,1），出口是在右下角（8,8）。根據給定的迷宮，找出一條從入口到出口的路徑。

解法一（深度優先遍歷，列印所有可行的路徑）：

#include <iostream>
using namespace std;

int maze[8][8] = {{0,0,0,0,0,0,0,0},{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},{0,1,0,0,0,0,1,0},
{0,1,0,1,1,0,1,0},{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},{0,1,1,1,1,1,1,0}};
//下、右、上、左
const int fx[4] = {1,0,-1,0};
const int fy[4] = {0,1,0,-1};
//maze[i
 
][j] = 3;//標識已走
//maze[i][j] = 2;//標識死衚衕
//maze[i][j] = 1;//標識牆
//maze[i][j] = 0;//標識可以走

//列印路徑
void printPath()
{
    for (int i=0;i<8;++i)
    {
        for (int j=0;j<8;++j)
        {
            if (3 == maze[i][j])
            {
                cout<<"V";
            }
            else
            {
                cout<<"*";
 

            }
        }
        cout<<endl;
    }
    cout<<endl;
}

void search(int i, int j)
{
    int newx;
    int newy;
    for (int k=0;k<4;++k)
    {
        newx = i+fx[k];
        newy = j+fy[k];
        //如果不是牆，且沒有走過
        if (newx>=0 && newx <8 && newy>=0 && newy<8 && 0 == maze[newx][newy])
 

        {
            maze[newx][newy] = 3;
            if (7 == newx && 7 == newy)
            {
                printPath();
                maze[newx][newy] = 0;
            }
            else
            {
                search(newx,newy);
            }       
        }
    }
    **//回溯的時候將此點標記未訪問，這樣下一條路徑也可以訪問**
    maze[i][j] = 0;
}

int main()
{
    maze[0][0] = 3;
    search(0,0);
    return 0;
}

執行結果：

解法二（廣度優先遍歷）：

#include <iostream>
#include <vector>
using namespace std;

int maze[8][8] = {{0,0,0,0,0,0,0,0},{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},{0,1,0,0,0,0,1,0},
{0,1,0,1,1,0,1,0},{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},{0,1,1,1,1,1,1,0}};
//下、右、上、左
const int fx[4] = {1,0,-1,0};
const int fy[4] = {0,1,0,-1};

struct sq{
    int x;
    int y;
    int pre;
};

//標記路徑，正確的點值賦為3
void markPath(const vector<sq> &q, int index)
{
    sq tmp = q[index];
    maze[tmp.x][tmp.y] = 3;
    if ( 0 == tmp.x && 0 == tmp.y )
    {
        return ;
    }
    else
    {
        markPath(q, tmp.pre);
    }
}

//列印路徑
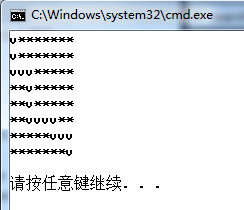
void printPath()
{
    for (int i=0;i<8;++i)
    {
        for (int j=0;j<8;++j)
        {
            if (3 == maze[i][j])
            {
                cout<<"v";
            }
            else
            {
                cout<<"*";
            }
        }
        cout<<endl;
    }
    cout<<endl;
}

//檢查點（i,j）是否滿足
bool check(int i, int j)
{
    if (i >= 0 && i<8 && j>=0 && j<8 && 0 == maze[i][j])
    {
        return true;
    }
    return false;
}

void search()
{

    //模仿佇列，之所以不用真正的佇列，因為後面需要通過下標對佇列進行隨機訪問
    vector<sq> q;
    int qh = 0;
    sq fnode;
    fnode.pre = -1;
    fnode.x = 0;
    fnode.y = 0;
    //標記已訪問
    maze[fnode.x][fnode.y] = -1;
    q.push_back(fnode);
    int qe = 1;
    sq tmp;
    while (qh != qe)
    {
        //出隊
        tmp = q[qh];
        ++qh;
        int newx, newy;
        for (int k=0;k<4;++k)
        {
            newx = tmp.x + fx[k];
            newy = tmp.y + fy[k];
            if (check(newx, newy))
            {
                sq n_node;
                n_node.pre = qh - 1;
                n_node.x = newx;
                n_node.y = newy;
                //入隊
                q.push_back(n_node);
                ++qe;
                //找到出口，列印
                if (7 == newx && 7 == newy)
                {
                    markPath(q, qe-1);
                    printPath();
                    return;
                }
            }
        }
        //maze[tmp.x][tmp.y] = -1;
    }
}

int main()
{
    maze[0][0] = 3;
    search();
    return 0;
}

執行結果：