圖 深度優先遍歷 廣度優先遍歷 非遞迴遍歷 圖解演算法過程
圖的鄰接矩陣表示
通常圖的表示有兩種方法:鄰接矩陣,鄰接表。
本文用鄰接矩陣實現,一是程式碼量更少,二是程式碼風格也更貼近C語言。但不論是圖的哪種實現方式,其基本的實現思想是不變的。
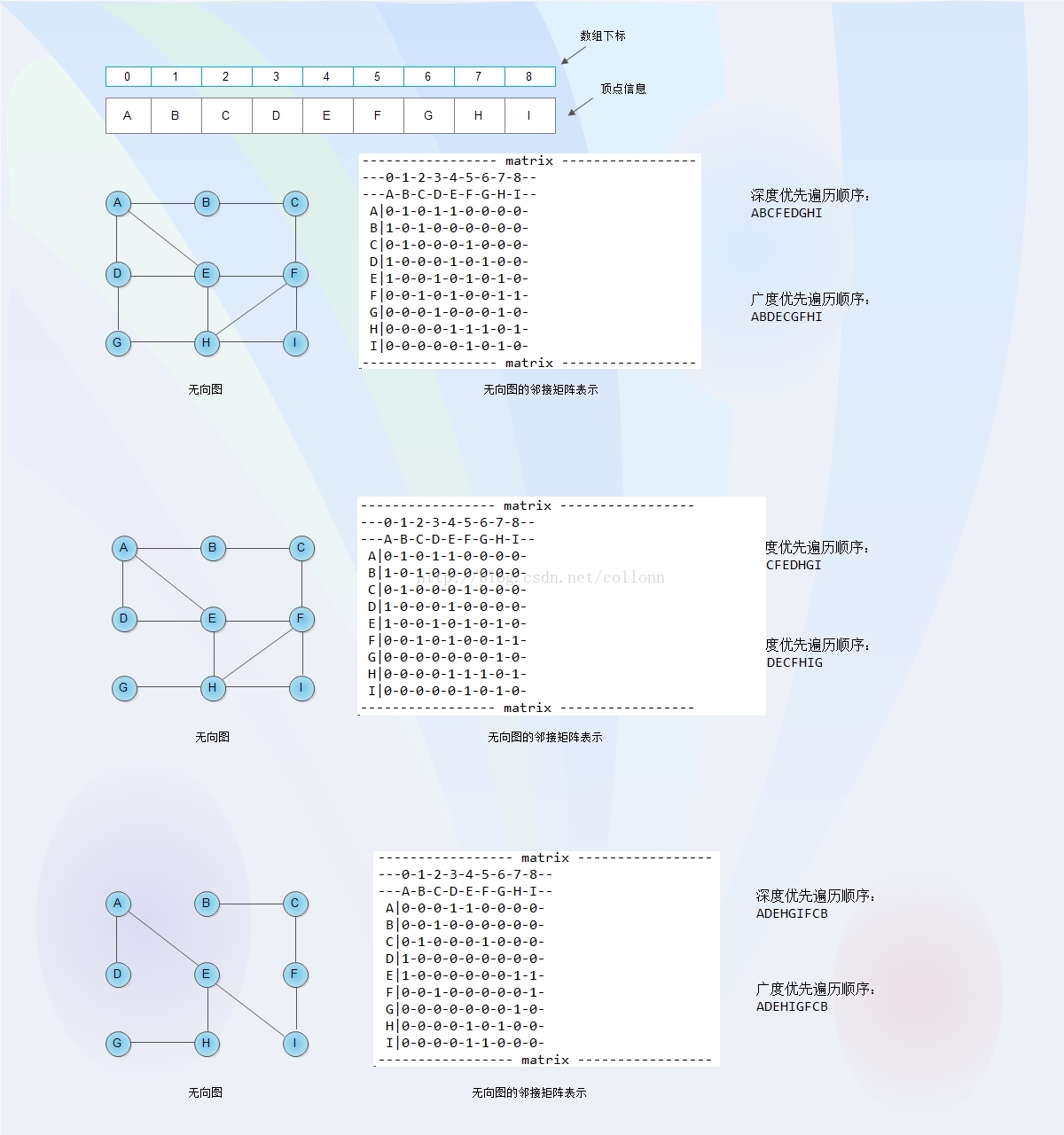
1:節點的資訊,我們用一維陣列a[n]來儲存,假設圖共有n個節點。
2:節點與節點間的關係,我們用二維陣列b[n][n]儲存。
3:b[i][j]表示,從i到j有向連通,b[j][i]表示從j到i有向連通,而當i=j時(矩陣的對角線上的元素),b[i][j]沒有實際意思,在遍歷時,我可以用來儲存定節點是否訪問過。
圖的深度優先遍歷
DFS類似於樹的先根遍歷,儘可能深的去訪問節點。
DFS演算法過程我們用到了遞迴的思想,如果還需要求出路徑,可以藉助棧來實現(後文會不斷的實現圖的各種演算法)。
步驟1:訪問節點,將該節點標記為已訪問。
步驟2:如果節點還有未標記的鄰接點,繼續步驟1,否則返回。
圖的廣度優先遍歷
BFS我們用佇列來實現。
步驟1:如果佇列為空,則返回,否則,取出佇列頭節點,將該節點標記為已訪問。
步驟2:同時,將該節點所有未標記的鄰接點,加入佇列尾,繼續步驟1。
圖的非遞迴遍歷
我們藉助棧來實現。
步驟1:如果棧為空,則退出程式,否則,訪問棧頂節點,但不彈出棧點節點。
步驟2:如果棧頂節點的所有直接鄰接點都已訪問過,則彈出棧頂節點,否則,將該棧頂節點的未訪問的其中一個鄰接點壓入棧,同時,標記該鄰接點為已訪問,繼續步驟1。
如下例子:
深度和廣度遍歷程式碼如下:
package com.collonn.algorithm; import java.util.LinkedList; import java.util.Queue; import java.util.Stack; /** * 無向圖,鄰接矩陣<br/> * 深度優先遍歷<br/> * 廣度優先遍歷<br/> */ public class GrfDfsBfs { private int total; private String[] nodes; private int[][] matirx; public GrfDfsBfs(int total, String[] nodes) { this.total = total; this.nodes = nodes; this.matirx = new int[total][total]; } private void printMatrix() { System.out.println("----------------- matrix -----------------"); System.out.println("---0-1-2-3-4-5-6-7-8--"); System.out.println("---A-B-C-D-E-F-G-H-I--"); for (int i = 0; i < this.total; i++) { System.out.print(" " + this.nodes[i] + "|"); for (int j = 0; j < this.total; j++) { System.out.print(this.matirx[i][j] + "-"); } System.out.print("\n"); } System.out.println("----------------- matrix -----------------"); } // 設定[i][i]位置處的元素值為0,0表示圖中的定點i未被訪問,1表示圖中的定點i已被訪問 private void resetVisited() { for (int i = 0; i < this.total; i++) { this.matirx[i][i] = 0; } } // 圖的深度優先遍歷(遞迴方法) private void dfsRecursive(int i) { // 如果已訪問,則返回 if (this.matirx[i][i] == 1) { return; } this.matirx[i][i] = 1; System.out.print(this.nodes[i]); for (int j = 0; j < this.total; j++) { // i=j時,[i][j]表示節點是否被訪問過,不參與dfs if (i == j) { continue; } if (this.matirx[i][j] == 1) { dfsRecursive(j); } } } // 圖的深度優先遍歷(用棧實現) private void dfsStack(Stack<Integer> stack) { // 如果已訪問,則返回 int k = -1; while(!stack.empty()){ k = stack.peek().intValue(); boolean needPop = true; for(int i = 0; i < this.total; i++){ if(this.matirx[k][i] == 1 && this.matirx[i][i] == 0){ stack.push(i); this.matirx[i][i] = 1; System.out.print(this.nodes[i]); needPop = false; break; } } if(needPop){ stack.pop(); } } } // 圖的廣度優先遍歷 private void bfsQueue(Queue<Integer> ls) { if (ls == null || ls.size() == 0) { return; } int i = ls.poll().intValue(); // 如果已訪問,則跳過該元素,繼續訪問佇列的下一個元素 if (this.matirx[i][i] == 1) { this.bfsQueue(ls); return; } this.matirx[i][i] = 1; System.out.print("" + this.nodes[i]); for (int j = 0; j < this.total; j++) { // i=j時,[i][j]表示節點是否被訪問過,不參與bfs if (i == j) { continue; } //如果頂點已訪問過,則不再加入佇列 if (this.matirx[i][j] == 1 && this.matirx[j][j] != 1) { ls.offer(j); } } // System.out.print("\n佇列元素:"); // for (Integer k : ls) { // System.out.print(k); // } // System.out.println(""); this.bfsQueue(ls); } // 初始化圖資料 // 0---1---2---3---4---5---6---7---8--- // A---B---C---D---E---F---G---H---I--- private void initGrf() { // A-B, A-D, A-E this.matirx[0][1] = 1; this.matirx[1][0] = 1; this.matirx[0][3] = 1; this.matirx[3][0] = 1; this.matirx[0][4] = 1; this.matirx[4][0] = 1; // B-C this.matirx[1][2] = 1; this.matirx[2][1] = 1; // C-F this.matirx[2][5] = 1; this.matirx[5][2] = 1; // D-E, D-G this.matirx[3][4] = 1; this.matirx[4][3] = 1; this.matirx[3][6] = 1; this.matirx[6][3] = 1; // E-F, E-H this.matirx[4][5] = 1; this.matirx[5][4] = 1; this.matirx[4][7] = 1; this.matirx[7][4] = 1; // F-H, F-I this.matirx[5][7] = 1; this.matirx[7][5] = 1; this.matirx[5][8] = 1; this.matirx[8][5] = 1; // G-H this.matirx[6][7] = 1; this.matirx[7][6] = 1; // H-I this.matirx[7][8] = 1; this.matirx[8][7] = 1; } // 初始化圖資料 // 0---1---2---3---4---5---6---7---8--- // A---B---C---D---E---F---G---H---I--- private void initGrf2() { // A-B, A-D, A-E this.matirx[0][1] = 1; this.matirx[1][0] = 1; this.matirx[0][3] = 1; this.matirx[3][0] = 1; this.matirx[0][4] = 1; this.matirx[4][0] = 1; // B-C this.matirx[1][2] = 1; this.matirx[2][1] = 1; // C-F this.matirx[2][5] = 1; this.matirx[5][2] = 1; // D-E this.matirx[3][4] = 1; this.matirx[4][3] = 1; // E-F, E-H this.matirx[4][5] = 1; this.matirx[5][4] = 1; this.matirx[4][7] = 1; this.matirx[7][4] = 1; // F-H, F-I this.matirx[5][7] = 1; this.matirx[7][5] = 1; this.matirx[5][8] = 1; this.matirx[8][5] = 1; // G-H this.matirx[6][7] = 1; this.matirx[7][6] = 1; // H-I this.matirx[7][8] = 1; this.matirx[8][7] = 1; } // 初始化圖資料 // 0---1---2---3---4---5---6---7---8--- // A---B---C---D---E---F---G---H---I--- private void initGrf3() { // A-D, A-E this.matirx[0][3] = 1; this.matirx[3][0] = 1; this.matirx[0][4] = 1; this.matirx[4][0] = 1; // B-C this.matirx[1][2] = 1; this.matirx[2][1] = 1; // C-F this.matirx[2][5] = 1; this.matirx[5][2] = 1; // E-H, E-I this.matirx[4][7] = 1; this.matirx[7][4] = 1; this.matirx[4][8] = 1; this.matirx[8][4] = 1; // F-I this.matirx[5][8] = 1; this.matirx[8][5] = 1; // G-H this.matirx[6][7] = 1; this.matirx[7][6] = 1; } public static void main(String[] args) { String[] nodes = new String[] { "A", "B", "C", "D", "E", "F", "G", "H", "I" }; GrfDfsBfs grf = new GrfDfsBfs(9, nodes); grf.initGrf(); grf.printMatrix(); System.out.println("------ 深度優先遍歷(遞迴)開始 ------"); grf.resetVisited(); grf.dfsRecursive(0); System.out.println(); System.out.println("------ 深度優先遍歷(遞迴)結束 ------"); System.out.println("------ 深度優先遍歷(棧)開始 ------"); grf.resetVisited(); Stack<Integer> stack = new Stack<Integer>(); stack.push(0); grf.matirx[0][0] = 1; System.out.print(grf.nodes[0]); grf.dfsStack(stack); System.out.println(); System.out.println("------ 深度優先遍歷(棧)結束 ------"); System.out.println("------ 廣度優先遍歷開始 ------"); grf.resetVisited(); Queue<Integer> queue = new LinkedList<Integer>(); queue.add(0); grf.bfsQueue(queue); System.out.println(); System.out.println("------ 廣度優先遍歷結束 ------"); } }
原創博文,轉載請註明出處。
右鍵,檢視圖片,看大圖。
相關推薦
【資料結構】鄰接矩陣表示法的圖的深度廣度優先遍歷遞迴和非遞迴遍歷
假設有以下結構的圖: 用鄰接矩陣表示如下: 因為他是無向圖,我們可以發現他的矩陣是對角對稱的。矩陣中每一行每一列都可以看成是一個頂點,矩陣中的元素表示著該頂點與其他頂點的關係,當元素的值為1說明它與對應列的頂點有邊相連,如果他們的值為0,表示他們沒有邊相
圖 深度優先遍歷 廣度優先遍歷 非遞迴遍歷 圖解演算法過程
圖的鄰接矩陣表示 通常圖的表示有兩種方法:鄰接矩陣,鄰接表。 本文用鄰接矩陣實現,一是程式碼量更少,二是程式碼風格也更貼近C語言。但不論是圖的哪種實現方式,其基本的實現思想是不變的。 1:節點的資訊,我們用一維陣列a[n]來儲存,假設圖共有n個節點。 2:節點與節點間的關係
資料結構之DFS遞迴與非遞迴遍歷鄰接表存圖
學習鄰接表存圖請看:https://blog.csdn.net/HPU_FRDHR/article/details/83957240 DFS (深度優先搜尋) 深度優先搜尋演算法(英語:Depth-First-S
二叉樹先序後序遞迴建立,前中後序層次非遞迴遍歷,以及統計葉子結點個數以及樹的深度
下面的程式碼實現了二叉樹的先序或者後序遞迴建立,然後實現了二叉樹的非遞迴的先序中序後序遍歷,還有層次遍歷,以及統計樹的葉子結點個數和樹的深度。其中非遞迴的先中後序遍歷用到了鏈棧,層次遍歷用到了佇列。 程式設計平臺為Visual Studio 2012,語言為C,但不是純C,
圖的dfs遞迴(非遞迴)遍歷和bfs遍歷(鄰接表)
1.深度優先遍歷是連通圖的一種遍歷策略.其基本思想如下: 設x是當前被訪問的頂點,在對x做過訪問的標記之後,選擇一條從x出發的未檢測過的邊(x,y),若發現頂點y已經訪問過了,則重新選擇另一條從x出發的未檢測過的邊,否則沿邊(x,y)到達未曾訪問過的y,對y訪問並將其標
利用棧結構實現二叉樹的非遞迴遍歷,求二叉樹深度、葉子節點數、兩個結點的最近公共祖先及二叉樹結點的最大距離
原文地址:http://blog.csdn.net/forbes_zhong/article/details/51227747 利用棧實現二叉樹的非遞迴遍歷,並求二叉樹的深度、葉子節點數、兩個節點的最近公共祖先以及二叉樹結點的最大距離,部分參考《劍指offer》這本書
圖的遍歷(鄰接矩陣的非遞迴實現)
#include<iostream> #include<cstring> #include<queue> using namespace std; typedef char TypeData; #define MAXVEX 100 #d
二叉樹非遞迴遍歷的通用演算法
二叉樹的3中遍歷策略,關鍵在於處理節點的時機不同:前序遍歷是遇到節點時處理,中序是處理完左節點後再處理,而後序是在處理完左右節點後再處理。 使用非遞迴方法實現時,除了記錄當前的節點的訪問棧,還需要記錄當前節點的狀態。對於每一個節點,我們用0來表示尚未處理左右子節點,1表示僅僅處理完畢左節點,2表
(原始碼,具體的細節請查閱相關資料)哈弗曼樹的構造以及非遞迴遍歷樹
寫了一點haffman樹的建立和二叉樹的非遞迴遍歷. 如果編寫程式碼的時候出現了,思維斷點,可以借鑑一下, 避免浪費一些不必要的時間. 我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔位符我是佔
(★★★)二叉樹非遞迴遍歷 (統一的解決思路)
轉載:【刷題】二叉樹非遞迴遍歷 stack<Node*> st; void preOrder(Node* root) { Node *cur = root; while (cur || !st.empty()) { while (
【演算法】二叉樹的遞迴和非遞迴遍歷(轉)
原文地址 【寫在前面】 二叉樹是一種非常重要的資料結構,很多其它資料結構都是基於二叉樹的基礎演變而來的。對於二叉樹,有前序、中序以及後序三種遍歷方法。因為樹的定義本身就 是遞迴定義,因此採用遞迴的方法去實現樹的三種遍歷不僅容易理解而且程式碼很簡潔。而對於樹的遍歷若採用非遞迴的方法,就要採
二叉樹的建立、遞迴,非遞迴遍歷
#include<bits/stdc++.h> using namespace std; typedef struct ListNode{ struct ListNode *Lchild, *Rchild; string str; ListNode():Lchild
C++ 二叉樹非遞迴遍歷(別貪心,一次迴圈訪問一個節點,前序遍歷2例外)
前序遍歷方法1: void preOrder1(BiNode * rootN) { if (rootN != nullptr) { stack<BiNode*> nodeSta; nodeSta.push(rootN); BiNode* curNode; wh
二叉樹的非遞迴遍歷和層次遍歷
資料結構 struct node{ int val; node *lchild,*rchild; }; 先序非遞迴遍歷 1) 訪問結點p,並將結點P入棧; 2) 判
二叉樹的非遞迴遍歷(先序、中序、後序和層序遍歷)
[前文] 二叉樹的非遞迴遍歷有 先序遍歷、中序遍歷 、後續遍歷 和 層序遍歷。 非遞迴演算法實現的基本思路:使用堆疊。而層序遍歷的實現:使用佇列。 如下圖所示的二叉樹: 前序遍歷順序為:ABCDE (先訪問根節點,然後先序遍歷其左子樹,最後先序遍歷
二叉樹的非遞迴遍歷---JAVA實現
二叉樹的遞迴遍歷方式是很簡單的,當需要用非遞迴的方式遍歷時,就需要藉助棧這種資料結構,以前序遍歷為例,其定義為先訪問根節點,再以前序方式訪問左子樹,再以前序遍歷方式訪問右子樹,這是個遞迴的定義。對於前序遍歷,最先訪問的是根,然後是根左邊的孩子,
樹的非遞迴遍歷
前序非遞迴遍歷 void preOrder2(BinTree *root) //非遞迴前序遍歷 { stack<BinTree*> s; BinTree *p=root; while(p!=NULL||!s.empty()) {
二叉樹的遞迴非遞迴遍歷
二叉樹定義結構: struct BtNode{ int data; BtNode * lchild; BtNode * rchild; }; 二叉樹有三種遍歷,前序遍歷,中序遍歷,後序遍歷 前序遍歷的順序是對每一棵樹(子樹),先訪問根節點,然後訪問左子樹,然後訪問右子樹 中序遍
C++ 二叉樹非遞迴遍歷
前序遍歷方法1: void preOrder1(BiNode * rootN) { if (rootN != nullptr) { stack<BiNode*> nodeSta;
使用java實現二叉樹的非遞迴遍歷
在前面的一片部落格中已經介紹了二叉樹遍歷的一些概念以及注意事項,如果有疑惑的可以回過頭看一看。 這裡我們主要討論的是使用非遞迴的演算法實現二叉樹的遍歷 前序遍歷: 思路: 1.使用一個棧來儲存元素,剛開始的時候將棧頂元素壓入棧 2.當棧不為空的時候做如下操作:彈