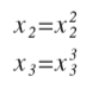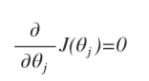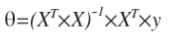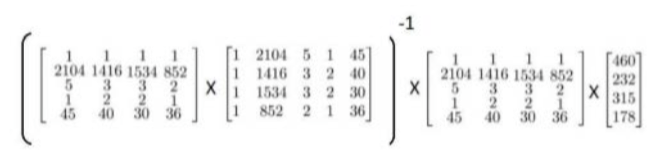上一次我們分享了多變數線性迴歸模型(Linear Regression with Multiple Variables)，這一次我們來討論一下多項式迴歸(Polynomial Regression)和正規方程(Normal Equation)。（我們還是討論房價預測的問題）

多項式迴歸

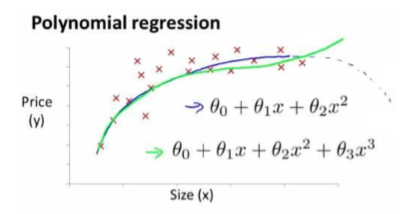
有時候，線性迴歸並不適用於所有全部的資料，我們需要曲線來適應我們的資料，比如一個二次方模型：

或者一個三次方模型：

這兩個模型我們在座標系繪圖如下：

通常情況，我們需要先觀察資料然後再去決定使用怎樣的模型來處理問題。

除此之外，我們還可以使 ：

這樣便將高階方程模型轉換成線性迴歸模型。這也算是特徵縮放(Features Scaling

PS ： 如果我們的模型採用多項式迴歸模型，在執行梯度下降演算法之前，特徵縮放是非常有必要的。

正規方程

到目前為止，我們學習討論的機器學習演算法，都是梯度下降演算法(Grandient Descent)。但是對於某些迴歸問題，還有一種更好的解決方案，正規方程。

正規方程是通過求解下面的方程來找出使得代價函式最小的引數：

假設我們的訓練特徵矩陣為X（包含了X0=1）並且我們的訓練集結果為向量 y ，則利用正規方程解出向量 :

標註：T表示矩陣X的轉置，-1 表示矩陣X的逆

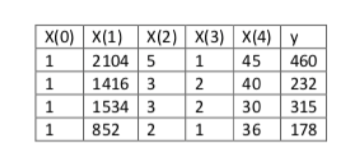
我們使用房價預測問題的資料：

資料包括四個特徵（不包括X0），我們加入X0=1，這時候我們使用正規方程方法來求解：

在Matlab中，正規方程寫作：pinv(X' * X)*X'*y

這裡有一個需要注意的地方，有些不可逆的矩陣（通常是因為特徵之間並不獨立，比如同時包含英尺為單位的尺寸和米為單位的尺寸這兩個特徵，也有可能是特徵數量大於訓練集的數量，比如有2000個特徵但是隻有1000個訓練集），正規方程方法是不能夠使用的。

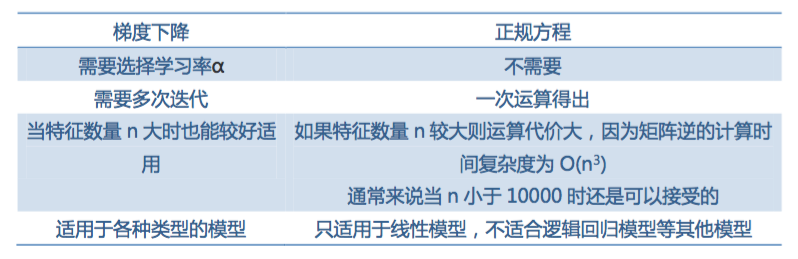
那麼我們現在有兩個機器學習的演算法了，一個是梯度下降，一個是正規方程，兩個方法比較如下：

至此，線性迴歸的問題我們就討論到這兒。下一階段我們將討論邏輯迴歸問題(Logistic Regression)。