概率語言模型及其變形系列(2)-LDA及Gibbs Sampling

阿新 • • 發佈：2019-02-08

本系列博文介紹常見概率語言模型及其變形模型，主要總結PLSA、LDA及LDA的變形模型及引數Inference方法。初步計劃內容如下

第三篇：LDA變形模型-Twitter LDA，TimeUserLDA，ATM，Labeled-LDA，MaxEnt-LDA等

第四篇：基於變形LDA的paper分類總結

第二篇 LDA及Gibbs Sampling

1 LDA概要

LDA是由Blei,Ng, Jordan 2002年發表於JMLR的概率語言模型，應用到文字建模範疇，就是對文字進行“隱性語義分析”（LSA），目的是要以無指導學習的方法從文字中發現隱含的語義維度-即“Topic”或者“Concept”。隱性語義分析的實質是要利用文字中詞項(term)的共現特徵來發現文字的Topic結構，這種方法不需要任何關於文字的背景知識。文字的隱性語義表示可以對“一詞多義”和“一義多詞”的語言現象進行建模，這使得搜尋引擎系統得到的搜尋結果與使用者的query在語義層次上match，而不是僅僅只是在詞彙層次上出現交集。

2 概率基礎

2.1 隨機生成過程及共軛分佈

要理解LDA首先要理解隨機生成過程。用隨機生成過程的觀點來看，文字是一系列服從一定概率分佈的詞項的樣本集合。最常用的分佈就是Multinomial分佈，即多項分佈，這個分佈是二項分佈拓展到K維的情況，比如投擲骰子實驗，N次實驗結果服從K=6的多項分佈。相應的，二項分佈的先驗Beta分佈也拓展到K維，稱為Dirichlet分佈。在概率語言模型中，通常為Multinomial分佈選取的先驗分佈是Dirichlet分佈，因為它們是共軛分佈，可以帶來計算上的方便性。什麼是共軛分佈呢？在文字語言模型的引數估計-最大似然估計、MAP及貝葉斯估計一文中我們可以看到，當我們為二項分佈的引數p選取的先驗分佈是Beta分佈時，以p為引數的二項分佈用貝葉斯估計得到的後驗概率仍然服從Beta分佈，由此我們說二項分佈和Beta分佈是共軛分佈。這就是共軛分佈要滿足的性質。在LDA中，每個文件中詞的Topic分佈服從Multinomial分佈，其先驗選取共軛先驗即Dirichlet分佈；每個Topic下詞的分佈服從Multinomial分佈，其先驗也同樣選取共軛先驗即Dirichlet分佈。

2.2 Multinomial分佈和 Dirichlet分佈

上面從二項分佈和Beta分佈出發引出了Multinomial分佈和Dirichlet分佈。這兩個分佈在概率語言模型中很常用，讓我們深入理解這兩個分佈。Multinomial分佈的分佈律如下

多項分佈來自N次獨立重複實驗，每次實驗結果可能有K種，式子中 $\vec{n}$ 為實驗結果向量，N為實驗次數， $\vec{p}$ 為出現每種實驗結果的概率組成的向量，這個公式給出了出現所有實驗結果的概率計算方法。當K=2時就是二項分佈，K=6時就是投擲骰子實驗。很好理解，前面的係數其實是列舉實驗結果的不同出現順序，即

$\frac{N!}{\prod_{i=1}^K n^{(k)}!}$

後面表示第K種實驗結果出現了 $n^{(k)}$ 次，所以是概率的相應次冪再求乘積。但是如果我們不考慮文字中詞出現的順序性，這個係數就是1。本文後面的部分可以看出這一點。顯然有

$\vec{p}$ 各維之和為1，所有 $n^{(k)}$ 之和為N。

Dirichlet分佈可以看做是“分佈之上的分佈”，從Dirichlet分佈上Draw出來的每個樣本就是多項分佈的引數向量 $\vec{p}$ 。其分佈律為

$\vec{\alpha}$ 為Dirichlet分佈的引數，在概率語言模型中通常會根據經驗給定，由於是引數向量 $\vec{p}$ 服從分佈的引數，因此稱為“hyperparamer”。 $\Delta(\vec{\alpha})$ 是Dirichlet delta函式，可以看做是Beta函式拓展到K維的情況，但是在有的文獻中也直接寫成 $B(\vec{\alpha})$ 。根據Dirichlet分佈在 $\vec{p}$ 上的積分為1（概率的基本性質），我們可以得到一個重要的公式

$\int_{\vec{p}}\prod_{k=1}^Kp_k^{\alpha_k - 1}d\vec{p} = \Delta(\vec{\alpha})$

這個公式在後面LDA的引數Inference中經常使用。下圖給出了一個Dirichlet分佈的例項

在許多應用場合，我們使用對稱Dirichlet分佈，其引數是兩個標量：維數K和引數向量各維均值 $\alpha = \frac{\sum\alpha_k}{K}$ . 其分佈律如下

關於Dirichlet分佈，維基百科上有一張很有意思的圖如下

File:LogDirichletDensity-alpha 0.3 to alpha 2.0.gif

這個圖將Dirichlet分佈的概率密度函式取對數

$\log (f(x_1,\dots, x_{K-1}; \alpha_1,\dots, \alpha_K)) = \log\left(\frac{1}{\mathrm{B}(\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}\right)= + \sum_{i=1}^K \alpha_i \log(x_i) - \sum_{i=1}^K \log(x_i) - \sum_{i=1}^K \log(\Gamma(\alpha_i)) + \log(\Gamma(\sum_{i=1}^K \alpha_i))$

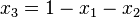並且使用對稱Dirichlet分佈，取K=3，也就是有兩個獨立引數 $x_1, x_2$ ，分別對應圖中的兩個座標軸，第三個引數始終滿足 $x_3 = 1-x_1-x_2$ 且 $\alpha_1=\alpha_2=\alpha_3=\alpha$ ，圖中反映的是 $\alpha$ 從0.3變化到2.0的概率對數值的變化情況。

3 unigram model

我們先介紹比較簡單的unigram model。其概率圖模型圖示如下

關於概率圖模型尤其是貝葉斯網路的介紹可以參見 Stanford概率圖模型（Probabilistic Graphical Model）— 第一講貝葉斯網路基礎一文。簡單的說，貝葉斯網路是一個有向無環圖，圖中的結點是隨機變數，圖中的有向邊代表了隨機變數的條件依賴關係。unigram model假設文字中的詞服從Multinomial分佈，而Multinomial分佈的先驗分佈為Dirichlet分佈。圖中雙線圓圈 $w_n$ 表示我們在文字中觀察到的第n個詞， $n\in [1,N]$ 表示文字中一共有N個詞。加上方框表示重複，就是說一共有N個這樣的隨機變數 $w_n$ 。 $\vec{p}$ 和 $\vec{\alpha}$ 是隱含未知變數，分別是詞服從的Multinomial分佈的引數和該Multinomial分佈的先驗Dirichlet分佈的引數。一般 $\vec{\alpha}$ 由經驗事先給定， $\vec{p}$ 由觀察到的文字中出現的詞學習得到，表示文字中出現每個詞的概率。

4 LDA

理解了unigram model之後，我們來看LDA。我們可以假想有一位大作家，比如莫言，他現在要寫m篇文章，一共涉及了K個Topic，每個Topic下的詞分佈為一個從引數為 $\vec{\beta}$ 的Dirichlet先驗分佈中sample出來的Multinomial分佈（注意詞典由term構成，每篇文章由word構成，前者不能重複，後者可以重複）。對於每篇文章，他首先會從一個泊松分佈中sample一個值作為文章長度，再從一個引數為 $\vec{\alpha}$ 的Dirichlet先驗分佈中sample出一個Multinomial分佈作為該文章裡面出現每個Topic下詞的概率；當他想寫某篇文章中的第n個詞的時候，首先從該文章中出現每個Topic的Multinomial分佈中sample一個Topic，然後再在這個Topic對應的詞的Multinomial分佈中sample一個詞作為他要寫的詞。不斷重複這個隨機生成過程，直到他把m篇文章全部寫完。這就是LDA的一個形象通俗的解釋。用數學的語言描述就是如下過程

轉化成概率圖模型表示就是

圖中K為主題個數，M為文件總數， $N_m$ 是第m個文件的單詞總數。 $\vec{\beta}$ 是每個Topic下詞的多項分佈的Dirichlet先驗引數， $\vec{\alpha}$ 是每個文件下Topic的多項分佈的Dirichlet先驗引數。 $z_{m,n}$ 是第m個文件中第n個詞的主題， $w_{m,n}$ 是m個文件中的第n個詞。剩下來的兩個隱含變數 $\vec{\theta}_m$ 和 $\vec{\phi}_k$ 分別表示第m個文件下的Topic分佈和第k個Topic下詞的分佈，前者是k維(k為Topic總數)向量，後者是v維向量（v為詞典中term總數）。

給定一個文件集合， $w_{m,n}$ 是可以觀察到的已知變數， $\vec{\alpha}$ 和 $\vec{\beta}$ 是根據經驗給定的先驗引數，其他的變數 $z_{m,n}$ ， $\vec{\theta}_m$ 和 $\vec{\phi}_k$ 都是未知的隱含變數，也是我們需要根據觀察到的變數來學習估計的。根據LDA的圖模型，我們可以寫出所有變數的聯合分佈

那麼一個詞 $w_{m,n}$ 初始化為一個term t的概率是

也就是每個文件中出現topic k的概率乘以topic k下出現term t的概率，然後列舉所有topic求和得到。整個文件集合的似然函式就是

5 用Gibbs Sampling學習LDA

5.1 Gibbs Sampling的流程

從第4部分的分析我們知道，LDA中的變數 $z_{m,n}$ ， $\vec{\theta}_m$ 和 $\vec{\phi}_k$ 都是未知的隱含變數，也是我們需要根據觀察到的文件集合中的詞來學習估計的，那麼如何來學習估計呢？這就是概率圖模型的Inference問題。主要的演算法分為exact inference和approximate inference兩類。儘管LDA是最簡單的Topic Model，但是其用exact inference還是很困難的，一般我們採用approximate inference演算法來學習LDA中的隱含變數。比如LDA原始論文Blei02中使用的mean-field variational expectation maximisation 演算法和Griffiths02中使用的Gibbs Sampling，其中Gibbs Sampling 更為簡單易懂。

Gibbs Sampling 是Markov-Chain Monte Carlo演算法的一個特例。這個演算法的執行方式是每次選取概率向量的一個維度，給定其他維度的變數值Sample當前維度的值。不斷迭代，直到收斂輸出待估計的引數。可以圖示如下

初始時隨機給文字中的每個單詞分配主題 $z^{(0)}$ ,然後統計每個主題z下出現term t的數量以及每個文件m下出現主題z中的詞的數量，每一輪計算，即排除當前詞的主題分配，根據其他所有詞的主題分配估計當前詞分配各個主題的概率。當得到當前詞屬於所有主題z的概率分佈後，根據這個概率分佈為該詞sample一個新的主題 $z^{(1)}$ 。然後用同樣的方法不斷更新下一個詞的主題，直到發現每個文件下Topic分佈 $\vec{\theta}_m$ 和每個Topic下詞的分佈 $\vec{\phi}_k$ 收斂，演算法停止，輸出待估計的引數 $\vec{\theta}_m$ 和 $\vec{\phi}_k$ ，最終每個單詞的主題 $z_{m,n}$ 也同時得出。實際應用中會設定最大迭代次數。每一次計算的公式稱為Gibbs updating rule.下面我們來推導LDA的聯合分佈和Gibbs updating rule。

5.2 LDA的聯合分佈

由LDA的概率圖模型，我們可以把LDA的聯合分佈寫成

第一項和第二項因子分別可以寫成

可以發現兩個因子的展開形式很相似，第一項因子是給定主題Sample詞的過程，可以拆分成從Dirichlet先驗中SampleTopic Z下詞的分佈 $\vec{\phi}_z$ 和從引數為 $\vec{\phi}_z$ 的多元分佈中Sample詞這兩個步驟，因此是Dirichlet分佈和Multinomial分佈的概率密度函式相乘，然後在 $\vec{\phi}_z$ 上積分。注意這裡用到的多元分佈沒有考慮詞的順序性，因此沒有前面的係數項。 $n_z^{(t)}$ 表示term t被觀察到分配topic z的次數， $n_m^{(k)}$ 表示topic k分配給文件m中的word的次數.此為這裡面還用到了2.2部分中匯出的一個公式

$\int_{\vec{p}}\prod_{k=1}^Kp_k^{\alpha_k - 1}d\vec{p} = \Delta(\vec{\alpha})$

因此這些積分都可以轉化成Dirichlet delta函式，並不需要算積分。第二個因子是給定文件，sample當前詞的主題的過程。由此LDA的聯合分佈就可以轉化成全部由Dirichlet delta函式組成的表示式

這個式子在後面推導Gibbs updating rule時需要使用。

5.3 Gibbs updating rule

得到LDA的聯合分佈後，我們就可以推導Gibbs updating rule，即排除當前詞的主題分配，根據其他詞的主題分配和觀察到的單詞來計算當前詞主題的概率公式

裡面用到了伽馬函式的性質

$\Gamma(z+1)=z \, \Gamma(z).$

同時需要注意到

這一項與當前詞的主題分配無關，因為無論分配那個主題，對所有k求和的結果都是一樣的，區別只在於拿掉的是哪個主題下的一個詞。因此可以當成常量，最後我們只需要得到一個成正比的計算式來作為Gibbs updating rule即可。

5.4 Gibbs sampling algorithm

當Gibbs sampling 收斂後，我們需要根據最後文件集中所有單詞的主題分配來計算 $\vec{\theta}_m$ 和 $\vec{\phi}_k$ ，作為我們估計出來的概率圖模型中的隱含變數。每個文件上Topic的後驗分佈和每個Topic下的term後驗分佈如下

可以看出這兩個後驗分佈和對應的先驗分佈一樣，仍然為Dirichlet分佈，這也是共軛分佈的性質決定的。

使用Dirichlet分佈的期望計算公式

我們可以得到兩個Multinomial分佈的引數 $\vec{\theta}_m$ 和 $\vec{\phi}_k$ 的計算公式如下

綜上所述，用Gibbs Sampling 學習LDA引數的演算法虛擬碼如下

關於這個演算法的程式碼實現可以參見

6 參考文獻及推薦Notes

本文部分公式及圖片來自 Parameter estimation for text analysis，感謝Gregor Heinrich詳實細緻的Technical report。看過的一些關於LDA和Gibbs Sampling 的Notes，這個是最準確細緻的，內容最為全面系統。下面幾個Notes對Topic Model感興趣的朋友也推薦看一看。

[1] Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag New York, Inc., Secaucus, NJ, USA, 2006.
[2] Gregor Heinrich. Parameter estimation for text analysis. Technical report, 2004.
[3] Wang Yi. Distributed Gibbs Sampling of Latent Topic Models: The Gritty Details Technical report, 2005.

[4] Wayne Xin Zhao, Note for pLSA and LDA, Technical report, 2011.

[5] Freddy Chong Tat Chua. Dimensionality reduction and clustering of text documents.Technical report, 2009.

[6] Wikipedia, Dirichlet distribution , http://en.wikipedia.org/wiki/Dirichlet_distribution

概率語言模型及其變形系列(2)-LDA及Gibbs Sampling

概率語言模型及其變形系列(2)-LDA及Gibbs Sampling

回歸模型效果評估系列2-MAE、MSE、RMSE、MAPE(MAPD)

神經概率語言模型

概率語言模型 Probabilistic Language Modeling (二) --- 模型估計演算法介紹

概率語言模型分詞方法

概率語言模型 Probabilistic Language Modeling (三) --- 訓練工具彙總

MIT自然語言處理第三講：概率語言模型（第四、五、六部分）

LDA的Gibbs Sampling求解

Java 多線程系列2——多線程的生命周期及生產消費者模型

智能合約語言 Solidity 教程系列2 - 地址類型介紹

《NLP漢語自然語言處理原理與實踐》第四章 NLP中的概率圖模型

自然語言處理系列-2-文字分類-傳統機器學習方法

自然語言處理系列-2-文字分類-深度學習-2

概率主題模型簡介，LDA基本思想

No.2 Pytorch 實現RNN語言模型

2 語言模型和詞向量 tensorflow詞向量

Chisel 語言（Scala）學習 2 例項化模型和向量操作

SDUTACM遞迴之漢諾塔系列2（基於C語言）

【中文分詞系列】 5. 基於語言模型的無監督分詞

[DeeplearningAI筆記]序列模型1.1-1.2序列模型及其數學符號定義

概率語言模型及其變形系列(2)-LDA及Gibbs Sampling

相關推薦