Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
  
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
  
• The wall is divided into segments and the width of each segment is one byte. 
  
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

The picture below illustrates the case of the sample input. 

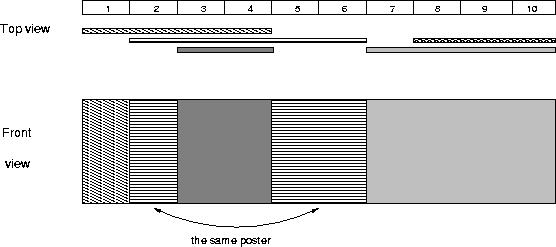
Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

題目大意：在一個公告欄上面張貼海報；張貼之後問可以看到幾張海報

題目分析：線段樹問題，但是如果以一個點為葉子節點的話就會超時妥妥的，所以採用離散化思想，首先將所有的點進行排序；用一個數組來進行對應，下標對應實際座標，下標對應的數字表示離散化之後的座標，通過離散化之後的座標可以建立線段樹

程式碼：

#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>

using namespace std;
struct code
{
    int r;int l;
}p[50005];
bool tree[50010*4];///這個樹的定義是是否這個區間被覆蓋；
void build ( int p,int l,int r)
{
    if ( l == r ) {tree[p] = true; return;}///將所有區間賦值為沒有被覆蓋
    int mid = ( l + r ) >> 1;
    build ( 2 * p, l, mid);
    build ( 2 * p + 1,mid + 1, r);
    tree[p] = tree[p*2]||tree[p*2+1];
}
bool post(int p,int l,int r, int sl, int sr)
{
    if ( tree[p] == 0 ) return false;
    if ( sl <= l&& sr >= r )
    {
        tree[p] = false;
        return true;
    }
    int mid = ( l + r ) >> 1;
    bool ok = 0;
    if ( sl <= mid ) ok = post( 2 * p , l , mid, sl , sr )||ok;///如果左邊區間有值的話在左邊區間查詢
    if ( sr > mid ) ok = post( 2 * p + 1, mid + 1, r, sl, sr )||ok;///如果右邊區間有值的話在右邊區間查詢
    tree[p] = tree[p*2]||tree[p*2+1];
    return ok;
}
int x[50005 << 1];
int hashs[10000002];
int posts;
int main()
{
    //freopen("in.txt","r",stdin);
    int test;
    scanf ( "%d",&test);
    while ( test > 0 )
    {
        test--;
        scanf("%d",&posts);
        int counts = 0;
        for ( int i = 0; i < posts; i++ )
        {
            scanf("%d %d",&p[i].l,&p[i].r);
            x[counts++] = p[i].l;
            x[counts++] = p[i].r;
        }
        sort(x,x+counts);
        counts = unique(x,x+counts) - x;///變數去重
        int node = 0;
        for ( int i = 0; i < counts; i++ )
        {
            hashs[x[i]] = node;///將所有的點進行對應，下標表示原來的座標，下標對應的數字應該是離散化之後的座標
            if ( i < counts - 1 )
            {
                if ( x [i+1] - x [i] == 1 )
                    node++;
                else
                    node+=2;
                ///如果兩個變數之間的座標差值超過1的話就要將中間的區間離散化進去；
                ///如果為1 10；1 4；5 10；和 1 10；1 4；6 10；如果第二種情況四和六之間差值大於1，如果不將中間的
                ///5離散化之後就會將第一種情況和第二種情況計算為2；
            }
        }
        build ( 1, 0,node);///建樹的時候要注意區間是從0到node的這個區間是左閉右閉；
        int ans = 0;
        for ( int i = posts-1; i >= 0; i--)
        ///這裡是將所有的海報倒著迴圈，也就是說如果前面的海報的所有地方被後面的海報佔的話就不能顯示出來了
        {
            if (post (1,0,node,hashs[p[i].l],hashs[p[i].r]))
                ans++;
        }

        printf ("%d\n",ans);

    }
}