目錄：

• 《劍指offer》面試題－topk演算法
• 搜尋熱詞關聯演算法
• 程式碼實現以及java學習

寫在前面

每次寫部落格都愛先扯點亂七八糟的東西，這是工作準備寫的第２篇部落格，之前寫過一篇hadoop入門，那裡還留下了一個搜尋引擎的demo沒有去完成，這次學習熱詞關聯剛好也是和搜尋引擎相關，所以藉此機會把這篇記錄下來，一方面花了３天來學習了這個內容，確實學到了不少東西，二來下次寫搜尋引擎的hadoop的demo時候可以把這個整合到一起，如果有空把關於搜尋的東西整合到一起，新增一些爬蟲相關的只是內容，就可以簡單的搭建一個搜尋引擎了，想想還是挺不錯的。好啦，我們來開始學習吧！

topK演算法

這個題目實現不難，在沒有什麼限制的情況下我們很快能得到答案。

解法１　排序

對陣列排序，然後找到最小的k個數字，這個思路和粗暴，實際上我們把問題轉化成了排序演算法，那麼合理的想法就是去找排序中時間複雜度最小的快排（Ｏ(nlgn)），這裡對於此方法有一個問題就是在於需要改變原陣列，如果題目中存在此種限制，自然是需要考慮其他演算法。

解法２　partition演算法

parition演算法，說起這個演算法可能對於演算法不太熟悉的同學真沒什麼印象，但是如果說快排大家肯定都知道了。我先貼一段java實現的程式碼給大家看一看。

//快速排序　雖然快排思想比較簡單，但是有些=還是需要注意一下勒，網上不少部落格的程式碼都有點小問題，所以自己寫了跑了下才貼出來。
 

    public static void qsort(int[] arr,int begin,int end) {

        int index = partition(arr, begin,end);

        if(begin >= end -1) {
            return; 
        }

        qsort(arr,begin,index-1);
        qsort(arr,index+1,end);

    }
//用一個哨兵來分割大於小於的兩部分
    private static int partition(int[] arr,int begin
 
,int end) {
        if(begin >= end) {
            return -1;
        }

        int pos = arr[begin];
        while(begin < end) {
            while(arr[end] >= pos && begin < end) {

                end --;
            }
            if(begin < end) {
                arr[begin] = arr[end];
            }
            while(arr[begin] <= pos && begin < end) {
                begin ++;
            }
            if(begin < end) {
                arr[end] = arr[begin];
            }
        }

        arr[begin] = pos;
        return begin;
    }

以上程式碼中有很重要的一塊就是partition，很多快排的寫法裡面沒有將其作為單獨的一個函式，他的思想就是取出一個哨兵，然後把大於他的放到一邊，小於他的放到另一邊。這樣如果我們按著這個思路，先找到一個數partition一次，判斷這個樹的最終位置是不是在k處，如果大於則找前面的部分（假設左小右大），如此直到我們找到第k個值的位置，此時k之前的都比k小，就得到了題解。下面我大概舉個例子，給大家一個形象的表示。
arr = 4,3,5,9,2,4,6 找到最小的３個值
partition1 2 3 4 9 5 4 6 index = 3 分了一次剛好index返回３，所以最小的是2 3 4，對沒毛病！
那我們現在來看一看這個演算法的時間複雜度，逆序的時候複雜度最高為O(n^2),如果是隨機的話，T(N) = T(T/2) + N,時間複雜度為O(N)。那麼我們可以在Ｏ(N）的時間複雜度把這個問題給解決了。這比上述排序好多了，因為針對上述排序中，我們每次都要把序列找到一個哨兵然後左右都要去排序，這個時候，我們只處理我們需要處理的部分，時間複雜度就降低了下來。雖然簡單，還是畫個圖表示一下下。如下圖，如果我們想要去找前３小的數字時，如果哨兵是５，那麼我們就可以不用管後面部分，只需要考慮前面綠色填充的數字，這樣節約了很多時間。

但是這個演算法仍然有點問題，同解法１，這個演算法會調整資料，當資料量不斷增加時，我們有時候希望能增量式的去處理，而不是每次有資料進來都乾坤大挪移，那麼我們需要考慮外部儲存來輔助這個演算法保證這個原陣列不會改變。

解法３ 外部儲存－小（大）根堆

我們日常也會遇到這樣的演算法例子，偶爾我們會用一個外部陣列來儲存，每次進來一個數字就判斷。比如我們想找一個數組裡面最大的３個數字，我開一個３空間的陣列，那麼我們遍歷一次原陣列，找到最大的３個依次放入，每次放入時和外部陣列比較一下，這樣也可以在O(N)時間內完成，且不改變原陣列，好啦。貌似我們對這個演算法已經瞭解的很深入了。
且慢，各位看客想一想，如果這個Ｎ非常非常大時候，如果我們要在幾百萬的資料中找前１０，那會有什麼不同麼。對於演算法複雜度來說，Ｏ(N)應該是不可避免了，至少每個數字都要遍歷到，但是對於大資料處理來說，複雜度中隱藏的時間常熟因子也是十分關鍵的。我們現在來分析一波，對於外部陣列，如果我們是找最大的Ｋ個數，那麼我們每次需要找到陣列中最小的，如果最小我們就要替換，所以會有替換操作。那麼對於一個無順序陣列的話，大概Ｏ(K)可以完成，然後我們演算法整體就是O(K*N),如果我們來維護一個有序陣列的話，開銷沒什麼區別。如果熟悉資料結構的同學，現在一定看出問題了，我們需要用堆來完成這些操作，取最小堆可以O(1)，來完成，而插入堆也可以在O(lgN)完成（平均），ＯＫ,資料量一大時候，這個差異是非常大的，先給大家看一個感性的認識，我沒有具體去算時間，只是進行了一下對比，heap為我自己實現的小根堆，orderarr是網上借鑑的別人實現的有序陣列。下面應該十分明顯了，k小時沒有啥區別，k的變大，這個差距會越來越大。

    int n = 3000000;
    int k = 100;
    orderarr程式執行時間： 16ms
    heap程式執行時間： 13ms

    int n = 3000000;
    int k = 100000;
    orderarr程式執行時間： 5137ms
    heap程式執行時間： 59ms

演算法不難，此處介紹一下思路即可，晚上有很多介紹堆思路的，演算法導論中有heapify來維護堆的，java中的優先佇列好像是用shiftup,shitfdown來維護insert操作，個人覺得都可以，思想都是一致的。大家有興趣可以翻翻我的github,文末給出，我把這些程式碼都放在裡面，有不對之處大家也可以指教。

public static void testHeap(int n,int k) {
        int[] arr = new int[n];
        Random random = new Random();

        for(int i=0;i<arr.length;i++) {
                arr[i] = random.nextInt();
            }

            int length = arr.length;
            MinHeap mHeap = new MinHeap();

            long startTime=System.currentTimeMillis();   //獲取開始時間 

            for(int i=0;i<length;i++) {
                if(i<=k-1) {
                    mHeap.insert(arr[i]);
                }else {
                    if(arr[i] > mHeap.getTop()) {
                        mHeap.removeTop();
                        mHeap.insert(arr[i]);
                    }
                }
            }
//      mHeap.show();
        long endTime=System.currentTimeMillis(); //獲取結束時間  
        System.out.println("heap程式執行時間： "+(endTime-startTime)+"ms");  

    }

熱詞搜尋提示

現在終於到正題了，之前半天都是在介紹演算法，現在也講講該演算法的應用，現在xx搜尋引擎公司需要根據使用者的輸入來給其他使用者做輸入提示，那麼我們有很多輸入詞條，現在需要提示熱度最高的。這實際就是一個topK問題，額外之處一個是操作物件不在是一個整數，而是一個鍵值對，另外一個問題是我們需要構建一顆trie樹來幫助我們找到需要排序的詞語。當然對於日誌資訊來說，資料是一條一條的，我們還需要用到hash表來幫我們進行統計。

第一步　hashMap統計

對於hash表來說，沒有特別要多說的，統計一個大資料量，如果記憶體夠的話，一張hash表無疑是很好的選擇，O(n)的時間就可以搞定，當然這個大資料也是有一個限制的，如果上Ｔ或者更大，那可能就需要想其他的辦法了。Ｇ級別的這個還是沒問題的。此處我們使用java中的hashMap來完成。

第二步　構建trie樹

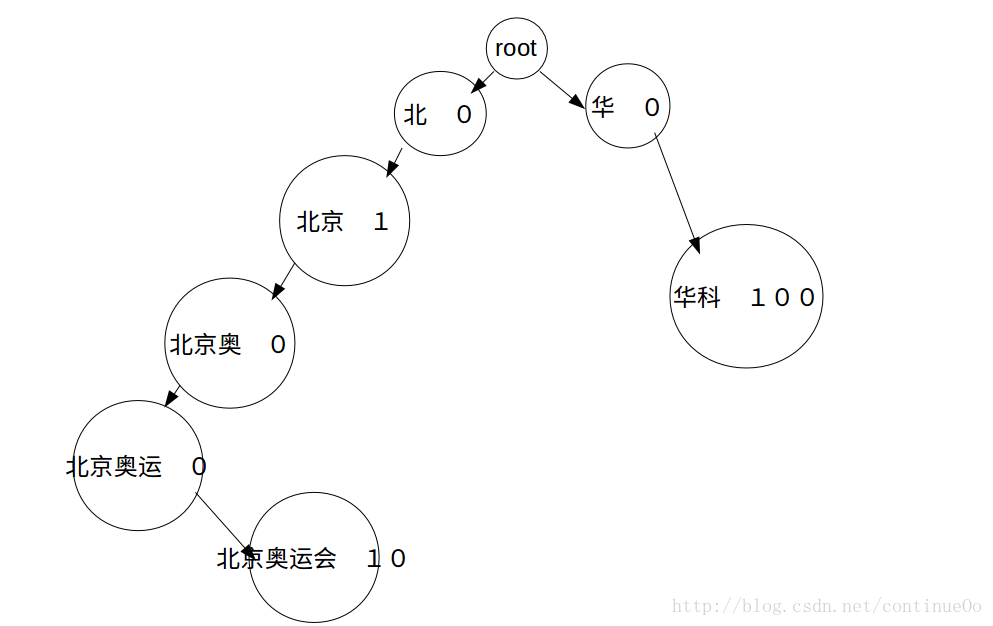
因為涉及到應用，當輸入“北”的時候，希望能提示“北京”，或者“北海”，不能提示“南京”吧，那麼我們需要有一顆字首樹來實現，每次找到輸入的節點的子樹，對子樹中的節點遍歷，取得最大的Ｋ個，為了方便，字首樹結構如下，每個節點放置到當前節點位置的所有字元，並且新增對應頻次，路過的詞語頻次為０，結構圖大致如下。

第三部　topK演算法

topK說的很多了，我們需要改成能針對鍵值對的就ＯＫ啦！　~^_^~

程式碼實現以及java學習

決策樹部分

下面是決策樹的實現，決策樹中學習到的一個比較重要的點就是需要自己實現一個迭代器，之前的陣列可以直接遍歷，ｆｏｒ迴圈就可以了，但是樹沒有這麼簡單，便需要實現一個iterator來幫助完成遍歷。

首先class需要實現Iterable介面，呼叫x.iterator()返回一個Iterator類，這個類通常含有2個方法,hasnext(),next()。結構如下，具體請檢視其他介紹，此處不贅述。
public class MyIteratorClass implements Iterable{

    @Override
    public Iterator iterator() {
        // TODO Auto-generated method stub
        return new MyIterator;
    }
    private class MyIterator implements Iterator<TrieNode>{
        @Override
        //返回是否還有下一個值
        public boolean hasNext() {
            return null;
        }

        @Override
        //返回下一個迭代的值
        public TrieNode next() {
            return null;
        }

import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import datastructure.TrieTree.TrieNode;

public class TrieTree implements Iterable{     
    private  TrieNode root;

    public static void main(String[] args) {
        TrieTree trieTree = new TrieTree();
        trieTree.insert("北京動物園", 2);
        trieTree.insert("北京天安門", 3);
        trieTree.insert("北京", 1);
        String word = "北京";
        TrieNode subTree = trieTree.getSubTreeByWord(word);
        Iterator<TrieNode> iterator = trieTree.iterator(subTree);
        while(iterator.hasNext()) {
            TrieNode node = iterator.next();
            System.out.println(node.value + " " + node.count);
        }
        //trieTree.showTrieTree();
    }

    public TrieNode getRoot() {
        return root;
    }

    public TrieTree() {
        root = new TrieNode("root",0);
    }

    public class TrieNode{
        private String value;
        private ArrayList<TrieNode> son;
        private int count; //當前路徑上統計數
        public TrieNode() {
            // TODO Auto-generated constructor stub
            this.value = "null";
            this.count = 0;
            this.son = new ArrayList<TrieNode>();
        }

        public TrieNode(String value,int count) {
            // TODO Auto-generated constructor stub
            this.value = value;
            this.count = count;
            this.son = new ArrayList<TrieNode>();
        }

        public String getValue() {
            return value;
        }

        public int getCount() {
            return count;
        }
    }




    //根據輸入獲取子樹
    public TrieNode getSubTreeByWord(String str) {
        return _getSubTreeByWord(root,str);
    }
    private TrieNode _getSubTreeByWord(TrieNode root,String str) {
        int sonNum = root.son == null? 0 :root.son.size();

        if(root.value.equals(str)) {
            return root;
        }

        for(int i=0;i<sonNum;i++) {
            TrieNode node = _getSubTreeByWord(root.son.get(i),str);
            if(node != null) {
                return node;
            }
        }
        return null;
    }

    //插入時，把count放在最後一個節點上
    public void insert(String str,int count) {
        _insertNode(root, str, count ,1);
    }
    private void _insertNode(TrieNode root,String str,int count ,int index) {
        int sonNum = root.son.size();
        int findFlag = 0;


        for(int i=0;i<sonNum;i++) {
            if(root.son.get(i).value.equals(str.substring(0, index))) {
                findFlag = 1;
                if(str.length() == index) {
                    root.son.get(i).count = count;
                    return;
                }else {
                    _insertNode(root.son.get(i), str, count ,index+1);
                }
                break;
            }
        }
        //遍歷之後沒有找到就建立一個
        if(findFlag == 0) {
        //  System.out.println(str.substring(0, index));
            String newValue = str.substring(0, index);
            int newCount = index != str.length() ? 0 : count;
            TrieNode sonNode = new TrieNode(newValue,newCount);
            root.son.add(sonNode);
            if(str.length() != index) {
                _insertNode(sonNode, str, count ,index+1);
            }
        }
    }

    //迴圈遍歷輸出字典樹內容
    public void showTrieTree() {
        _showTrieTree(root);
    }
    private void _showTrieTree(TrieNode root) {
        System.out.println(root.value + root.count);
        int sonNum = root.son.size();
        for(int i=0;i<sonNum;i++) {
            _showTrieTree(root.son.get(i));
        }
    }


    @Override
    public Iterator<TrieNode> iterator() {
        // TODO Auto-generated method stub
        return new TrieTreeIterator();
    }


    public Iterator<TrieNode> iterator(TrieNode itrRoot) {
        // TODO Auto-generated method stub
        return new TrieTreeIterator(itrRoot);
    }

    private class TrieTreeIterator implements Iterator<TrieNode>{
        private TrieNode next;
        private  Queue<TrieNode> queue;

        public TrieTreeIterator() {
            // TODO Auto-generated constructor stub
            next = root;
            queue = new LinkedList<TrieNode>();
            if(next == null) {
                return;
            }
        }

        public TrieTreeIterator(TrieNode itrRoot) {
            // TODO Auto-generated constructor stub
            next = itrRoot;
            queue = new LinkedList<TrieNode>();
            if(next == null) {
                return;
            }
        }

        @Override
        public boolean hasNext() {
            // TODO Auto-generated method stub
            int sonNum = next.son.size();
            for(int i=0;i<sonNum;i++) {
                queue.add(next.son.get(i));
            }
            if(queue.isEmpty()) {
                return false;
            }else {
                return true;
            }

        }

        @Override
        public TrieNode next() {
            // TODO Auto-generated method stub

            next = queue.remove();
            return next;
        }

    }

}  

Heap部分

此處借鑑了網友的程式碼，但是不記得哪裡抄來的了，抱歉。
這裡學到的比較重要的東西就是泛型的使用，對於這份程式碼來說，是適用與int的，但是我想拿這份程式碼來做鍵值對的處理，利用泛型和提供的Comparator就可以很方便的實現程式碼的複用。此處我定義了鍵值對的型別，提供了一些基礎方法。然後出現了另外一個重要的問題，那就是關於物件複製的問題，這裡學習了深克隆的方式，如果setRoot方法不傳入clone(),則只是傳入了索引，而不是對堆內進行賦值，這樣邏輯上有誤。所以這裡傳入一定是clone的內容。關於clone有深淺之分，這裡我使用了序列化的方式，下面這部落格寫的不錯，推一推。
克隆學習：https://www.cnblogs.com/Qian123/p/5710533.html

//程式碼複用可以學習的地方

//這是之前的程式碼
int[] arr = new int[n]
//此處省略，很多，這裡重點在於描述差異之處
mHeap.setRoot(arr[i]);

//這是修改後的程式碼
KeyPair<String, Integer> tempKeyPair = new KeyPair<String, Integer>("", 0);
mHeap.setRoot(tempKeyPair.clone());
//建立heap來做鍵值對比較
Comparator<KeyPair<String, Integer>> comp = new Comparator<KeyPair<String, Integer>>() {  
            @Override
            public int compare(KeyPair<String, Integer> o1, KeyPair<String, Integer> o2) {
                // TODO Auto-generated method stub
                return o2.getValue() - o1.getValue();
            }  
        };  

//克隆可以學習的部分，序列化方式克隆。

public class KeyPair<K, V> implements Serializable {
    private K key;
    private V value;

    public KeyPair clone() {
            KeyPair outer = null;
            try { // 將該物件序列化成流,因為寫在流裡的是物件的一個拷貝，而原物件仍然存在於JVM裡面。所以利用這個特性可以實現物件的深拷貝
                ByteArrayOutputStream baos = new ByteArrayOutputStream();
                ObjectOutputStream oos = new ObjectOutputStream(baos);
                oos.writeObject(this);
                // 將流序列化成物件
                ByteArrayInputStream bais = new ByteArrayInputStream(baos.toByteArray());
                ObjectInputStream ois = new ObjectInputStream(bais);
                outer = (KeyPair) ois.readObject();
            } catch (IOException e) {
                e.printStackTrace();
            } catch (ClassNotFoundException e) {
                e.printStackTrace();
            }
            return outer;
          }
    ｝

public class Heap<T> {  

    /** 
     * 以陣列形式儲存堆元素 
     */  
    private T[] heap;  

    /** 
     * 用於比較堆中的元素。c.compare(根,葉子) > 0。  
     * 使用相反的Comparator可以建立最大堆、最小堆。 
     */  
    private Comparator<T> c;  

    public Heap(T[] a, Comparator<T> c) {  
        this.heap = a.clone();  
        this.c = c;  
        buildHeap();  
    }  

    /** 
     * 返回值為i/2 
     *  
     * @param i 
     * @return 
     */  
    private int parent(int i) {  
        return (i - 1) >> 1;  
    }  

    /** 
         * 
     * 返回指定節點的left子節點陣列索引。相當於2*(i+1)-1 
         * 
     *  
     * @param i 
     * @return 
     */  
    private int left(int i) {  
        return ((i + 1) << 1) - 1;  
    }  

    /** 
     * 返回指定節點的right子節點陣列索引。相當於2*(i+1) 
     *  
     * @param i 
     * @return 
     */  
    private int right(int i) {  
        return (i + 1) << 1;  
    }  

    /** 
     * 堆化 
     *  
     * @param i 
     *           堆化的起始節點 
     */  
    private void heapify(int i) {  
        heapify(i, heap.length);  
    }  

    /** 
     * 堆化， 
     *  
     * @param i 
     * @param size 堆化的範圍 
     */  
    private void heapify(int i, int size) {  
        int l = left(i);  
        int r = right(i);  
        int next = i;  
        if (l < size && c.compare(heap[l], heap[i]) > 0)  
            next = l;  
        if (r < size && c.compare(heap[r], heap[next]) > 0)  
            next = r;  
        if (i == next)  
            return;  
        swap(i, next);  
        heapify(next, size);  
    }  


    /** 
     * 對堆進行排序 
     */  
    public void sort() {  
        // buildHeap();  
        for (int i = heap.length - 1; i > 0; i--) {  
            swap(0, i);  
            heapify(0, i);  
        }  
    }  

    /** 
     * 交換陣列值 
     *  
     * @param arr 
     * @param i 
     * @param j 
     */  
    private void swap(int i, int j) {  
        T tmp = heap[i];  
        heap[i] = heap[j];  
        heap[j] = tmp;  
    }  

    /** 
     * 建立堆 
     */  
    private void buildHeap() {  
        for (int i = (heap.length) / 2 - 1; i >= 0; i--) {  
            heapify(i);  
        }  
    }  

    public void setRoot(T root) {  
        heap[0] = root;  
        heapify(0);  
    }  

    public T root() {  
        return heap[0];  
    }  

    public T getByIndex(int i) {
        if(i<heap.length) {
            return heap[i];
        }
        return null;
    }
｝

總結

上面貼出了測試資料和最終結果，以上程式碼估計跑不通，貼出來是為了突出重點，如果想看跑，可以follow我的github，上面有完整例項，另外還有一些問題沒有解決完全，一個是大資料下的測試，另外有一個就是互動問題，因為考慮到後面還會寫相關搜尋引擎的板塊，所以這裡先不急著完善，以後有機會再做互動和完整測試。

哈，寫了３個多小時，終於總結完了～，看完有收貨的小夥伴，記得贊一個噢～。我們一起天天學演算法～