漫談計算機組成原理(九)定點數及定點數的運算
本文講什麼?
在計算機中,小數點並沒有用專門的器件去表示,而是按照一種約定的方式,統一儲存在暫存器單元中的。算數邏輯運算單元(ALU)是CPU的組成部分,負責算數和邏輯的運算。那麼,ALU究竟是如何工作的呢?
這就是本文主要探討的內容:
- 什麼是定點數?
- 定點數的位移、加、減、乘、除運算是如何進行的?
定點數是啥?
從字面意思來理解,“定點數”就是“點”不動的數。那麼究竟是什麼“點”不動呢?沒錯,就是“小數點”。
在上一講我們說道,不論是整數還是小數,都是有小數點的。整數的小數點表示在最後一位數字的後面,而小數的小數點標識在真值的符號位後面。如圖所示: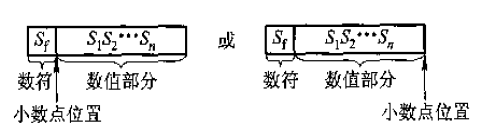
除了定點數,還有一種數叫做“浮點數”,浮點數將在下一講展開介紹。
定點數的運算
好了,介紹完定點數的基本概念以後,我們展開講定點數的位移運算和四則運算。定點數的四則運算實際上要比我們想象的複雜的多。
機器並不像人,一眼就知道二二得四,他需要知道2的定點表示形式,然後兩個定點數相乘,相乘是有一定的過程的,經過了這個過程,才能得到結果的二進位制數,最終輸出給我們。我們要做的,就是了解加減乘除究竟經歷了什麼樣子的過程。
定點數的位移運算
不要看移位運算簡單,但是它在計算機的運算中的地位是舉足輕重的。沒有移位運算,也就沒有後面的乘除法,乘除法就是在移位運算和加減運算的配合下實現的。
移位運算的規則:雖然正數和負數的移位運算規則不相同,但是相同之處在於移位後正數和負數的符號不變。那麼規則就變成了移位運算時,符號位不動,數值位按照如下規則進行移位。
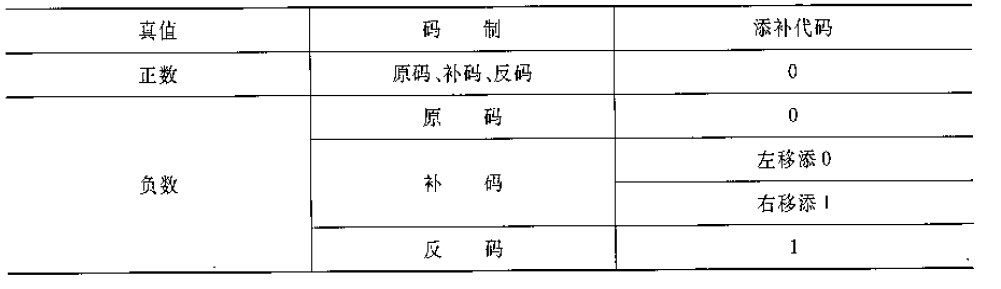
舉個例子:
將+26的原碼、補碼和反碼分別左移一位
結果是:[26]原 = [26]反 = [26]補 = 0,0011010,根據規則,原碼、反碼、補碼左移一位的結果是:0,010100將-26的原碼、反碼、補碼分別左移一位
[-26]原 = 1,0011010,左移一位:1,0110100
[-26]反 = 1,1100101,左移一位:1,1001011
[-26]補 = 1,1100110,左移一位:1,100110
移位的運算是不是很簡單?只需要根據規則來就可以了。重點在下面的幾種運算中。
定點數的加法與及減法
定點數的加減運算只需要記住一個原則:加法直接加,減法先變為加法後再計算。
什麼意思呢?比如[A+B]補 = [A+B]補,[A-B]補 = [A]補
來看兩個例子:
A = -1001,B = -0101,求[A+B]補
[A+B]補 = [A]補 + [B]補,[A]補 = 1,0111,[B]補 = 1,1011,所以最終的結果是:11,0010,但是這並非我們的最終結果,最終結果應該丟掉第一個1,即1,0010.為什麼呢?這涉及到一個模2運算的問題,如果不想深究只需要記住,一個數只能有一個符號位不是嗎?A = -1001,B=-0101.求[A-B]補
[A-B]補 = [A]補 + [-B]補,[A]補=1,0111,[-B]補=0,0101(求法:[-B]補等於[B]補符號位和各位取反,末位加一),這樣得到最終的結果,丟棄掉多餘的位即可。
溢位的判斷:如果計算機的機器字長為4,那麼能夠表示的真值範圍在-8~+7之間,如果兩個數相加減,跳出了這個範圍,則為溢位。
那麼應當如何判斷溢位呢?
原則:
- 不論加法還是減法,只要實際參與運算的兩個數的符號相同,但是與最終的結果的符號相反,則為溢位。比如我們的第一個例子,兩個參與運算的數的符號相同,且和最終結果的符號也相同,則這種情況就不是溢位。
- 最終結果的兩位符號位如果相同,則無溢位,如果不同則溢位,還是第一個例子,計算後的結果是11,0010,兩位符號位相同,沒有溢位。
定點數的乘法
乘法的運算方式形成過程,我推薦大家看看計算機專業的教材,即唐朔飛老師的《計算機組成原理》。本文奔著實用性的角度,不會過度發掘計算方法的推導過程,因為我的解釋並不如教材上的好。至於真正的計算,不能說是優於教材,最起碼你你能夠快速上手計算,如果你做到了,那麼我的目的也就達到了。
定點數乘法的計算方式:
原碼一位乘
- 說明:有A*B,令初始部分積為0,分別取A、B的絕對值A’、B’。乘數為B’,取乘數最後一位,如果是0,則部分積加0;如果是1,則部分積加A’。加法操作執行完成後,部分積右移一位,繼續執行上述操作,直到原有乘數的所有位均被用完。最後一步的加法執行完成後,右移一位,形成最終結果。最終結果的正負由二者的符號的異或決定。
單純的說你可能會有點懵逼,我們來結合一個實際的例子看看。 - 例:A = 0.1101,B = 0.1011,求A*B。
為了方便,我們將上述的計算過程放入表格中進行計算,表格如下:
乘數一欄的上部分數字暫時不用管,仔細看一下運算步驟,和我總結的對比,仔細體會即可。
- 說明:有A*B,令初始部分積為0,分別取A、B的絕對值A’、B’。乘數為B’,取乘數最後一位,如果是0,則部分積加0;如果是1,則部分積加A’。加法操作執行完成後,部分積右移一位,繼續執行上述操作,直到原有乘數的所有位均被用完。最後一步的加法執行完成後,右移一位,形成最終結果。最終結果的正負由二者的符號的異或決定。
原碼兩位乘:原碼兩位乘有運算規則,和一位乘有著類似的地方,但是不盡相同。原碼兩位乘是用兩位乘數的部分來決定新的部分如何形成的運算方式。兩個二進位制數共有四種形態:00,01,10,11,可以表示不同的移位方式以及加法的方式(下面會看到)。再加上一位標誌位C,就能實現更加複雜的操作。如圖所示:

有了上面的規則,就能夠很輕易的根據原碼一位乘做出原碼兩位乘,計算過程:初始化部分積為0,寫入乘數,標誌位置為0.判斷乘數的後兩位以及標誌位滿足何種關係,呼叫相應的方法移位並設定標誌位,最後的結果向右移動兩位,根據x和y的符號的異或確定符號。有必要說明的是,兩位乘需預留出3位符號位。給出個例子:- 例子:設x=0.111111,y=-0.111001,用原碼兩位乘求出[x*y]原
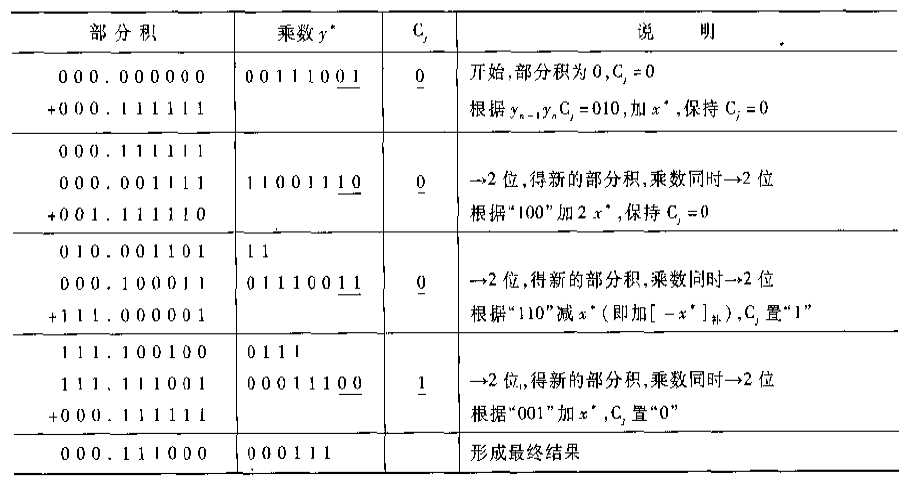
這樣就非常容易理解了。
- 例子:設x=0.111111,y=-0.111001,用原碼兩位乘求出[x*y]原
補碼乘法:補碼一位乘與原碼一位乘類似,區別在於,當乘數為正時,補碼乘法運算方法與原碼一位乘運算方式相同;當乘數為負數時,補碼一位乘前半部分同樣和原碼一位乘相同,不同之處是在運算完成後,需要把最終結果加上[-x]補用於校驗,才能得到最終的結果。這部分的推導同樣可以參見教科書。下面給出一個例子:
- 例子:[x]補 = 0.1101,[y]補 = 1.0101,求[x*y]補。由於[y]補為負數則需要在最終的結果加上[-x]補用於校驗。
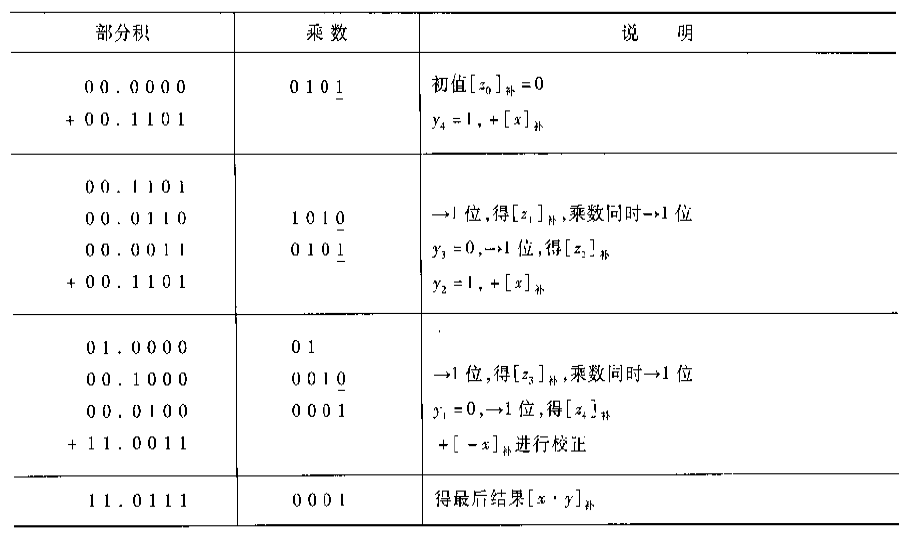
- 例子:[x]補 = 0.1101,[y]補 = 1.0101,求[x*y]補。由於[y]補為負數則需要在最終的結果加上[-x]補用於校驗。
補碼比較法:相信有了前面的基礎,直接給出規則你就能夠解決問題了,補碼比較法的運算規則如下:

給出例子:[x]補 = 0.1101,[y]補 = 0.1011.運算過程如下: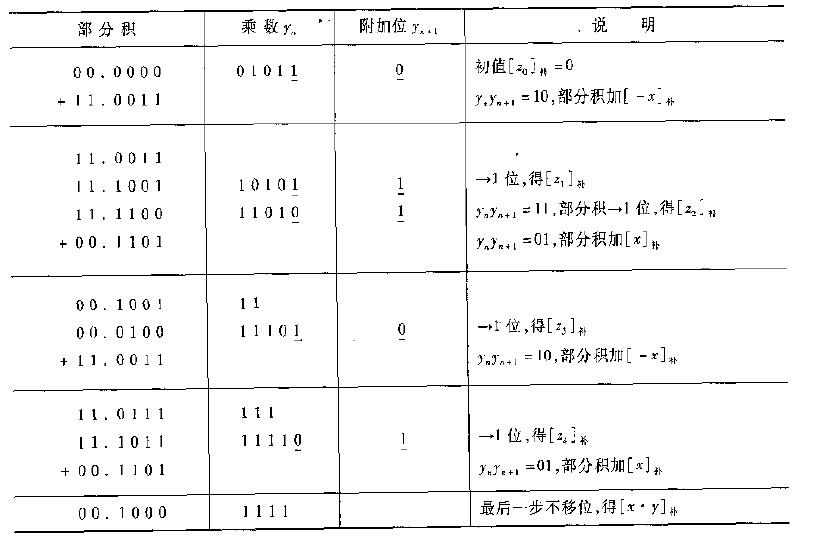
補碼兩位乘:補碼兩位乘和上面的方式沒有太多的區別,主要就是兩位乘採用三位符號位,三位判斷位(乘數的位),有了運算規則,做出題目簡直太簡單了。

例子:[x]補=0.0101,[y]補=1.0101,求[x*y]補。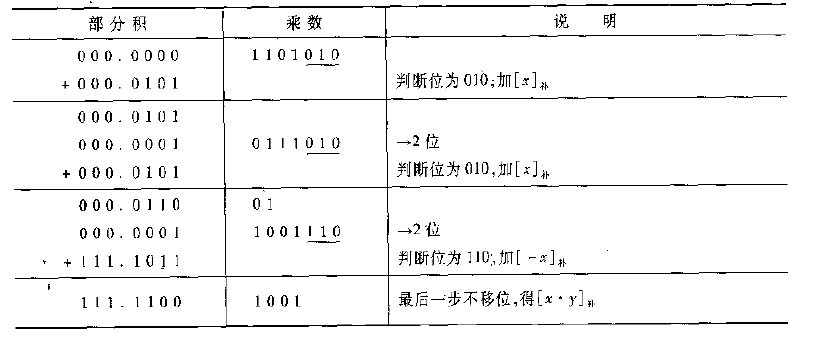
定點數的除法
這篇文章的內容已經比較多了,為了方便讀者消化知識,除法的講解放在下一篇文章中,敬請期待。
結語
如果你喜歡我的文章,請關注我的微信公眾號“最高許可權位元流”吧!
【參考文獻】《計算機組成原理》,唐朔飛。
