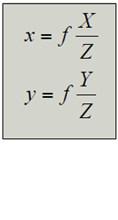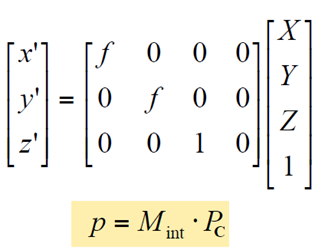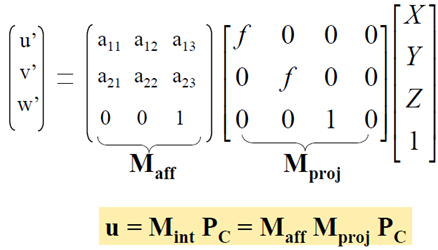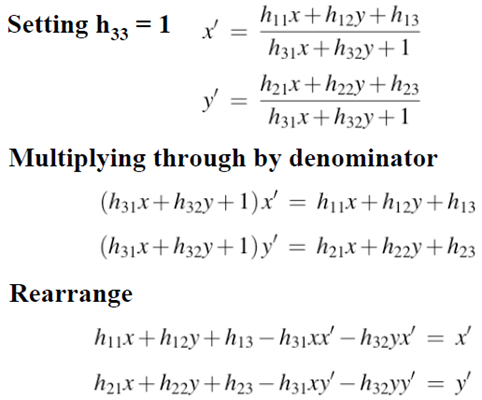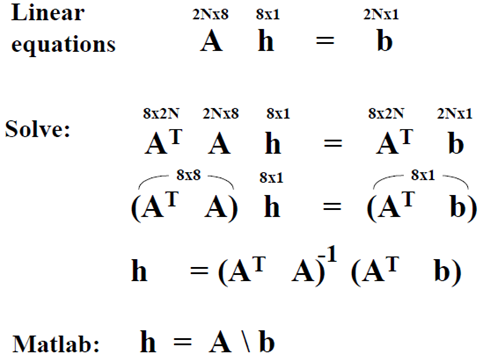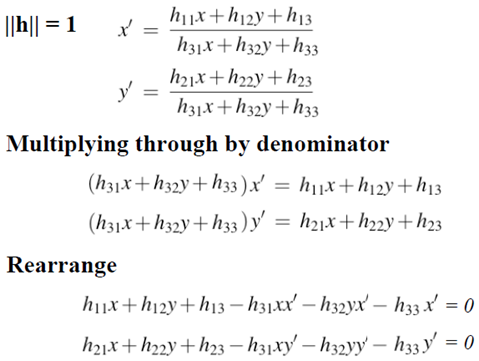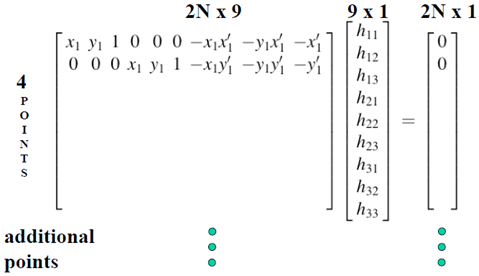轉載：http://blog.csdn.NET/yvonnezju/article/details/40982192

這一篇，要搞清楚兩個概念，Planar Homography （共麵點成像）& Epipolar Geometry（對極幾何）

Now，Start！

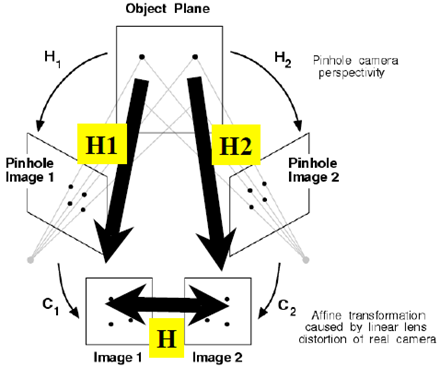
先補充Homography的概念，簡單來說Homography（單應性），說的是投影的時候可以逆過來找，比如,一個物體可以通過旋轉相機鏡頭獲取兩張不同的照片(這兩張照片的內容不一定要完全對應,部分對應即可),我們可以把單應性設為一個二維矩陣M,那麼照片1乘以M就是照片2. 這有著很多實際應用，比如影象校正、影象對齊或兩幅影象之間的相機運動計算（旋轉和平移）等。一旦旋轉和平移從所估計的單應性矩陣中提取出來，那麼該資訊將可被用來導航或是把3D物體模型插入到影象或視訊中，使其可根據正確的透視來渲染，並且成為原始場景的一部分（請見

具體的解釋可以戳wiki。

一、共麵點成像

思路：同一物理點，不同成像面之間的關係。

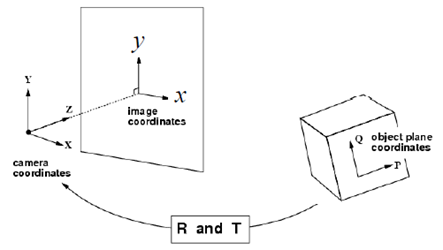
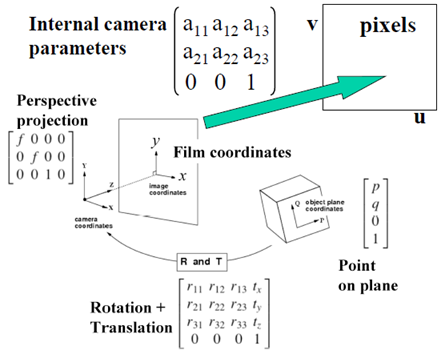
在前面已經討論了三維物體成像過程，相比之下，還有一種稍簡單的情況——平面成像，即所有的物點都處在同一個平面上，我們有理由相信，這種情況下的成像關係是一般立體成像的一種特例。

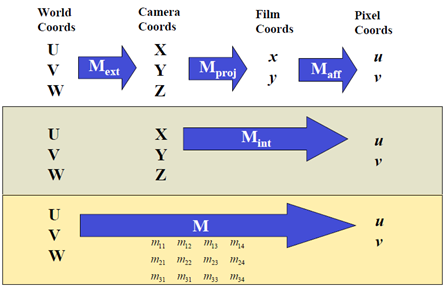
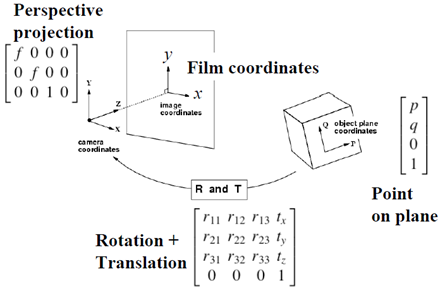
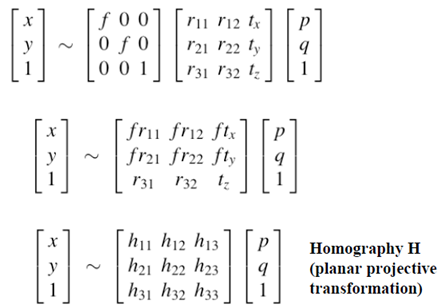
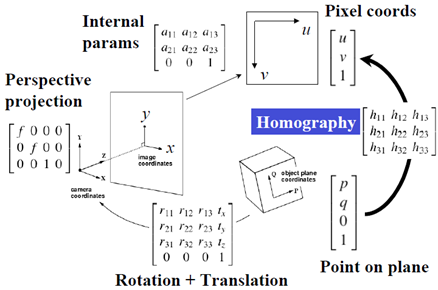
先回顧一下一般的單體成像過程

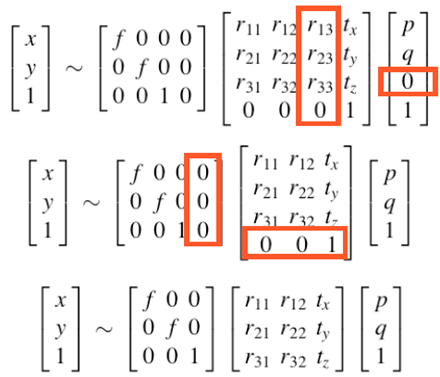
對於共面的物點，在恰當的世界座標系中，可以令其中一個座標值為0，不妨設第三維座標為0，圖示如下：

由於物點的第三維座標為0，整個成像過程的矩陣表示會得到簡化。

可以簡化為一個3X3的矩陣，稱之為Homography矩陣，該矩陣是可逆的!!

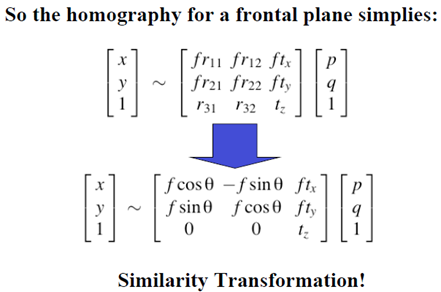
對於正前方的物體平面(垂直於光軸)，成像關係將更進一步簡化。

將共面物點經成像之後，再變換為數字影象(u,v)

研究共麵點成像有什麼意義呢？

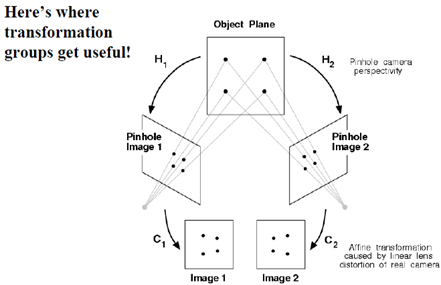
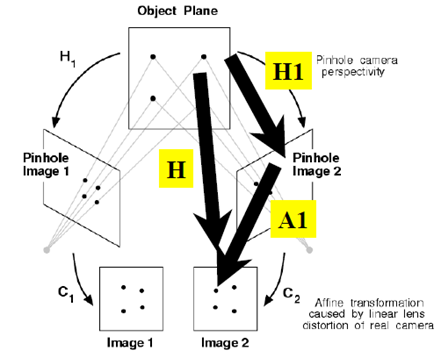
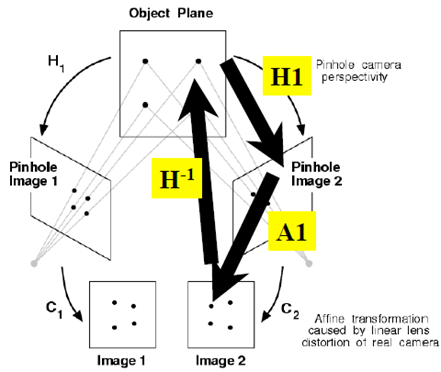
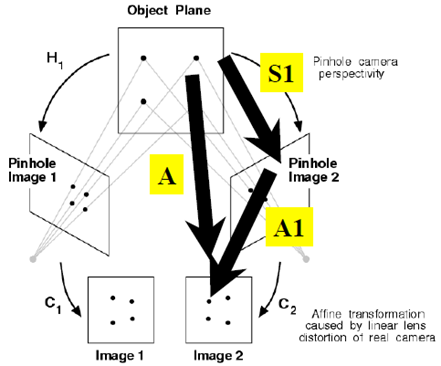
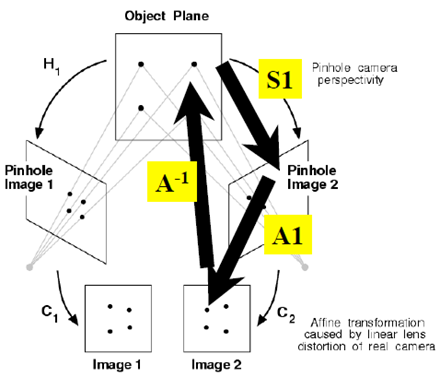
原來是為了研究兩幅圖之間的關係!共麵點成像過程總結如下：

應用之一：消除透視投影的失真

應用之二：影象拼接

在這些應用中，需要解決兩個關鍵問題：

1. 如何確定兩幅影象之間的變換關係(需要多少個已知點？如何計算？)

2. 如何生成新的畫素點，即在拉伸或拼接之後，需要生成新的畫素點。

選擇第一種約束關係

可以寫線上性方程組或矩陣的形式

在實際求解變換矩陣時，需要考慮數值計算的問題。

R.Hartley: “In Defense of the Eight Point Algorithm”
Observation: Linear estimation of projective transformation parameters from point correspondences often suffer from poor “conditioning” of the matrices involves. This means the solution is sensitive to noise in the points (even if there are no outliers).
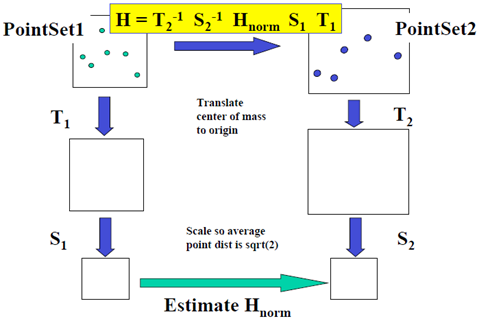
To get better answers, precondition the matrices by performing a normalization of each point set by:
• translating center of mass to the origin
• scaling so that average distance of points from origin is sqrt(2).
• do this normalization to each point set independently

採用第二種約束關係

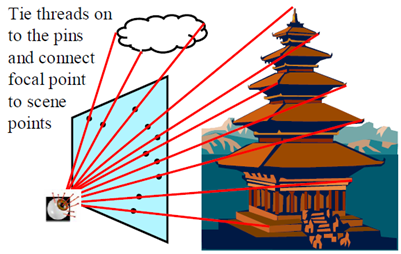
　　先思考一個問題：用兩個相機在不同的位置拍攝同一物體，如果兩張照片中的景物有重疊的部分，我們有理由相信，這兩張照片之間存在一定的對應關係，本節的任務就是如何描述它們之間的對應關係，描述工具是對極幾何 ，它是研究立體視覺的重要數學方法。

　　要尋找兩幅影象之間的對應關係，最直接的方法就是逐點匹配，如果加以一定的約束條件對極約束(epipolar constraint)，搜尋的範圍可以大大減小。

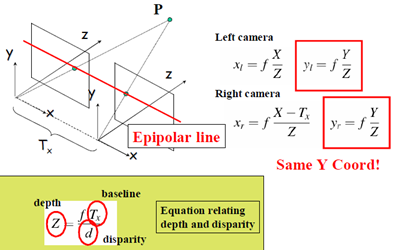
　　先回顧簡單的立體成像系統

對極約束的圖示

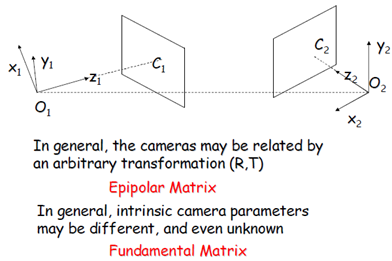
更一般的立體成像關係：兩個相機的座標無任何約束關係，相機的內部引數可能不同，甚至是未知的。要刻畫這種情況下的兩幅影象之間的對應關係，需要引入兩個重要的概念——對極矩陣(Epipolar Matrix)和基本矩陣(Fundamental Matrix)。

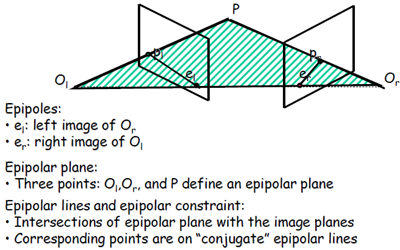
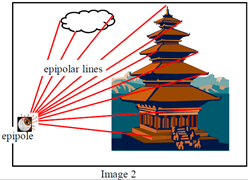
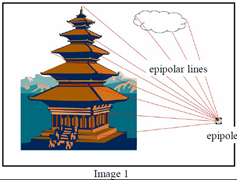
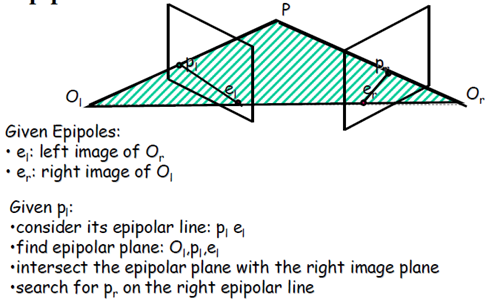
對極幾何中的重要概念（參考下圖）：

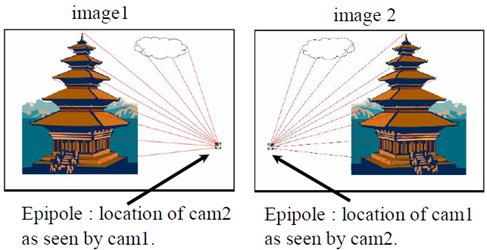
極點：極點el:右相機座標原點在左像平面上的像；極點er:左相機座標原點在右像平面上的像

極平面：由兩個相機座標原點Ol、Or和物點P組成的平面

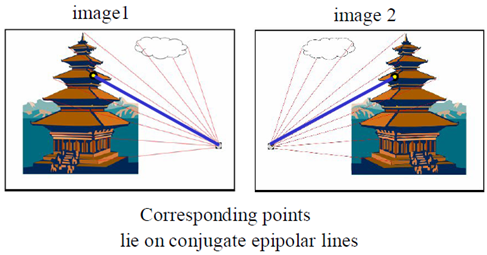
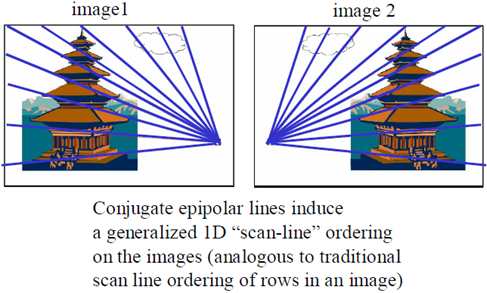
級線：極平面與兩個像平面的交線，即plel和prer

級線約束：兩極線上點的對應關係

有點煩人，先轉移一下話題：What would Pinhead’s eye look like close up?

如果兩個人同時看這一景物，將是什麼樣的呢？

再回到對極幾何圖上來，通過上面幾幅圖示，利用對極幾何的約束關係，我們可以：

1. 找到物點P在左像平面上的像點pl；

2. 畫出極線plel；

3. 找到極平面Olplel與右像平面的交線，即得極線prer；

4. 像點pl的對應點一定在極一prer上。

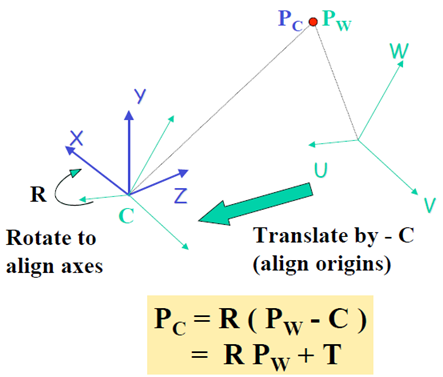
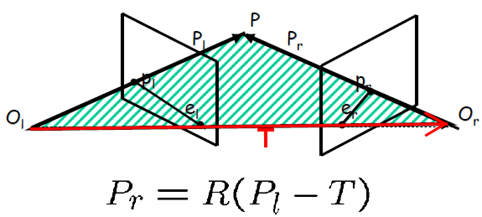
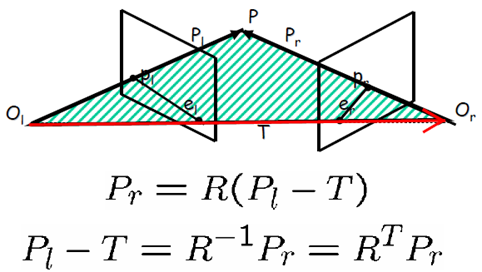
兩個相機座標系之間的關係為

由於R是正交矩陣，因此可寫為

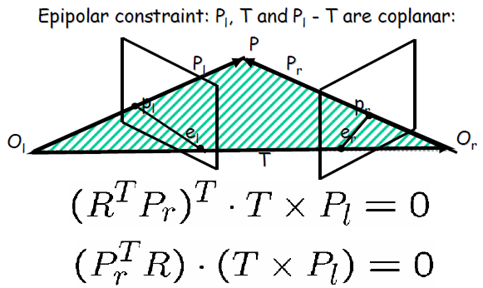
三向量共面，它們的混合積為零(混合積對應於有向體積)

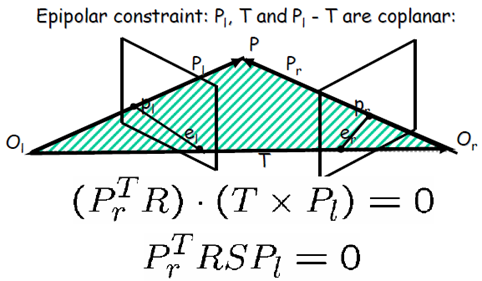
將向量乘(叉乘)寫成矩陣的形式

通過進一步的改寫，可以得到左像點和右像點之間約束關係(非常簡單、漂亮)

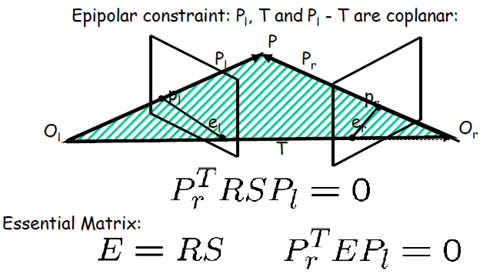
顯然，左像點pl和右像點pr是通過矩陣E=RS來約束的，我們稱矩陣E為本質矩陣(Essential Matrix)，它的基本性質有：

• has rank 2(秩為2)

• depends only on the EXTRINSIC Parameters (R & T)(僅依賴於外部引數R和T)