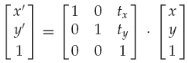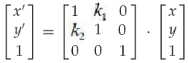Matrix主要用於對平面進行平移(Translate)，縮放(Scale)，旋轉(Rotate)以及斜切(Skew)操作。
為簡化矩陣變換，Android封裝了一系列方法來進行矩陣變換；其中包括：
set系列方法：setTranslate，setScale，setRotate，setSkew；設定，會覆蓋之前的引數。
pre系列方法：preTranslate，preScale，preRotate，preSkew；矩陣先乘，如M' = M * T(dx, dy)。
post系列方法：postTranslate，postScale，postRotate，postSkew；矩陣後乘，如M' = T(dx, dy) * M。
通過將變換矩陣與原始矩陣相乘來達到變換的目的，例如：
平移（x'=x+tx；y'=y+ty）：

縮放（x'=sx*x；y'=sy*y）：

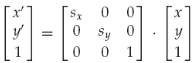
旋轉（x'=cosβ*x-sinβ*y；y'=sinβ*x+cosβ*y）：

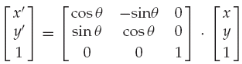
選擇需要用到如下的三角函式的公式：
①sin(α+β)=sinαcosβ+cosαsinβ
②cos(α+β)=cosαcosβ-sinαsinβ
公式①可以由單位圓方法或托勒密定理推匯出來。
推導過程參見：http://blog.sina.com.cn/s/blog_58260f420100c03j.html

斜切（x'=x+k1*y；y'=k2*x+y）：

//原始碼檔案：external\skia\legacy\src\core\SkMatrix.cpp

#define SK_Scalar1      (1.0f)
#define kMatrix22Elem   SK_Scalar1
typedef float   SkScalar;
#define SkScalarMul(a, b)       ((float)(a) * (b))

enum {
    kMScaleX, kMSkewX, kMTransX,
    kMSkewY, kMScaleY, kMTransY,
    kMPersp0, kMPersp1, kMPersp2
};

void SkMatrix::reset() {
    fMat[kMScaleX] = fMat[kMScaleY] = SK_Scalar1; //其值為1
    fMat[kMSkewX]  = fMat[kMSkewY] =
    fMat[kMTransX] = fMat[kMTransY] =
    fMat[kMPersp0] = fMat[kMPersp1] = 0; //其值，全為0
    fMat[kMPersp2] = kMatrix22Elem; //其值為1
    this->setTypeMask(kIdentity_Mask | kRectStaysRect_Mask);
}

void SkMatrix::setTranslate(SkScalar dx, SkScalar dy) {
    if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
        fMat[kMTransX] = dx; //以新值dx覆蓋原值，原值無效了
        fMat[kMTransY] = dy;

        fMat[kMScaleX] = fMat[kMScaleY] = SK_Scalar1; //其值為1
        fMat[kMSkewX]  = fMat[kMSkewY] = 
        fMat[kMPersp0] = fMat[kMPersp1] = 0; //其值，全為0
        fMat[kMPersp2] = kMatrix22Elem; //其值為1

        this->setTypeMask(kTranslate_Mask | kRectStaysRect_Mask);
    } else {
        this->reset();
    }
}

bool SkMatrix::preTranslate(SkScalar dx, SkScalar dy) {
    if (this->hasPerspective()) {
        SkMatrix    m;
        m.setTranslate(dx, dy);
        return this->preConcat(m); //矩陣的先乘運算
    }
    
    if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
        fMat[kMTransX] += SkScalarMul(fMat[kMScaleX], dx) +
                          SkScalarMul(fMat[kMSkewX], dy); //先乘，需要矩陣運算過
        fMat[kMTransY] += SkScalarMul(fMat[kMSkewY], dx) +
                          SkScalarMul(fMat[kMScaleY], dy);

        this->setTypeMask(kUnknown_Mask | kOnlyPerspectiveValid_Mask);
    }
    return true;
}

bool SkMatrix::postTranslate(SkScalar dx, SkScalar dy) {
    if (this->hasPerspective()) {
        SkMatrix    m;
        m.setTranslate(dx, dy);
        return this->postConcat(m); //矩陣的後乘運算
    }
    
    if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
        fMat[kMTransX] += dx; //後乘，直接加新值dx即可
        fMat[kMTransY] += dy;
        this->setTypeMask(kUnknown_Mask | kOnlyPerspectiveValid_Mask);
    }
    return true;
}

bool SkMatrix::preConcat(const SkMatrix& mat) { //矩陣的先乘運算(this在前）
    // check for identity first, so we don't do a needless copy of ourselves
    // to ourselves inside setConcat()
    return mat.isIdentity() || this->setConcat(*this, mat); //矩陣運算
}

bool SkMatrix::postConcat(const SkMatrix& mat) { //矩陣的後乘運算（this在後）
    // check for identity first, so we don't do a needless copy of ourselves
    // to ourselves inside setConcat()
    return mat.isIdentity() || this->setConcat(mat, *this); //矩陣運算
}
 

Matrix的初始值：
[sx, k1, 0]
[k2, sy, 0]
[0,   0,  1]
setTranslate(2, 3)後：
[sx, k1, 2]
[k2, sy, 3]
[0,   0,  1]
上面set後，再preTranslate(4, 5)：
[sx, k1, 2][1, 0, 4]  [sx, k1, sx*4+k1*5+2]
[k2, sy, 3][0, 1, 5]=[k2, sy, k2*4+sy*5+3]
[0,   0,   1][0, 0, 1]  [0,  0,  1]
上面set後，再postTranslate(4, 5)後：
[1, 0, 4][sx, k1, 2]  [sx, k1, 2+4]
[0, 1, 5][k2, sy, 3]=[k2, sy, 5+3]
[0, 0, 1][0,   0,   1]  [0,   0,  1]