序：博弈是資訊學和數學試題中常會出現的一種型別，演算法靈活多變是其最大特點，而其中有一類試題更是完全無法用常見的博弈樹來進行解答。 尋找必敗態即為針對此類試題給出一種解題思路。

此類問題一般有如下特點：

1、博弈模型為兩人輪流決策的非合作博弈。即兩人輪流進行決策，並且兩人都使用最優策略來獲取勝利。 2、博弈是有限的。即無論兩人怎樣決策，都會在有限步後決出勝負。 3、公平博弈。即兩人進行決策所遵循的規則相同。

理論鋪墊：

1、定義P-position和N-position：其中P代表Previous，N代表Next。直觀的說，上一次move的人有必勝策略的局面是P-position，也就是“先手必敗”，現在輪到move的人有必勝策略的局面是N-position，也就是“先手可保證必勝”。

（1）.無法進行任何移動的局面（也就是terminal position）是P-position；

（2）.可以移動到P-position的局面是N-position；

（3）.所有移動都導致N-position的局面是P-position。

2、P/N狀態有如下性質：

（1）、若面臨末狀態者為獲勝則末狀態為勝態否則末狀態為必敗態。
（2）、一個局面是勝態的充要條件是該局面進行某種決策後會成為必敗態。
（3）、一個局面是必敗態的充要條件是該局面無論進行何種決策均會成為勝態

3、P點： 即必敗點，某玩家位於此點，只要對方無失誤，則必敗；

   N點： 即必勝點，某玩家位於此點，只要自己無失誤，則必勝。

4、取石子游戲演算法實現

步驟1:將所有終結位置標記為必敗點（P點）；

步驟2: 將所有一步操作能進入必敗點（P點）的位置標記為必勝點（N點）

步驟3:如果從某個點開始的所有一步操作都只能進入必勝點（N點） ，則將該點標記為必敗點（P點） ；

步驟4: 如果在步驟3未能找到新的必敗（P點），則演算法終止；否則，返回到步驟2

/*

a.如果當前是P點，那麼一步（向前）可以走到的都是N點

b.如果當前點未標明P/N屬性，那麼看看該點向後走是不是都只能到達N點，如果是，那麼該點是P點。

c.如果該點是N點，倒無法確定什麼。

如果沒辦法標一個點，那麼異常結束。

*/

幾種常見型別詳解：

一、巴什博弈

1、問題模型：只有一堆n個物品，兩個人輪流從這堆物品中取物，規定每次至少取一個，最多取m個，最後取光者得勝。

2、解決思路：當n=m+1時，由於一次最多隻能取m個，所以無論先取者拿走多少個，後取者都能夠一次拿走剩餘的物品，後者取勝，所以當一方面對的局勢是n%(m+1)=0時，其面臨的是必敗的局勢。所以當n=（m+1)*r+s，（r為任意自然數，s≤m)時,如果先取者要拿走s個物品，如果後取者拿走x（≤m)個，那麼先取者再拿走m+1-k個，結果剩下（m+1）（r-1）個，以後保持這樣的取法，那麼先取者肯定獲勝。總之，要保持給對手留下（m+1）的倍數，就能最後獲勝。

3、變形：條件不變，改為最後取光的人輸。

結論：當（n-1）%（m+1）==0時後手勝利。

4、題目練習：HDOJ：2188 2149 1846

二、威佐夫博奕

1、問題模型：有兩堆各若干個物品，兩個人輪流從某一堆或同時從兩堆中取同樣多的物品，規定每次至少取一個，多者不限，最後取光者得勝。

2、解決思路：A：設（ai,bi）（ai ≤bi  ,i=0，1，2，…,n)表示兩堆物品的數量並稱其為局勢，如果甲面對（0，0），那麼甲已經輸了，這種局勢我們稱為奇異局勢。前幾個奇異局勢是：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。任給一個局勢（a，b），如下公式判斷它是不是奇異局勢： ak =[k（1+√5）/2]，bk= ak + k  （k=0，1，2，…,n 方括號表示取整函式）。（證明見百度百科）

3、滿足上公式的局勢性質：

（1）任何自然數都包含在一個且僅有一個奇異局勢中。

     由於ak是未在前面出現過的最小自然數，所以有ak > ak-1 ，而 bk= ak + k > ak-1 + k-1 = bk-1 > ak-1 。所以性質成立。

（2）任意操作都可將奇異局勢變為非奇異局勢。

    若只改變奇異局勢（ak，bk）的某一個分量，那麼另一個分量不可能在其他奇異局勢中，所以必然是非奇異局勢。如果使（ak，bk）的兩個分量同時減少，則由於其差不變，且不可能是其他奇異局勢的差，因此也是非奇異局勢

（3）採用適當的方法，可以將非奇異局勢變為奇異局勢。

     假設面對的局勢是（a,b），若 b = a，則同時從兩堆中取走 a 個物體，就變為了奇異局勢（0，0）；如果a = ak ，b &gt; bk，那麼，取走b  – bk個物體，即變      為奇異局勢；如果 a = ak ，  b < bk ,則同時從兩堆中拿走 ak – ab – ak個物體,變為奇異局勢（ ab – ak , ab – ak+ b – ak）；如果a > ak ，            b= ak + k,則從第一堆中拿走多餘的數量a – ak 即可；如果a < ak ，b= ak + k,分兩種情況，第一種，a=aj （j < k）,從第二堆裡面拿走 b – bj 即可； 第      二種，a=bj （j < k）,從第二堆裡面拿走 b – aj 即可。

4、結論：兩個人如果都採用正確操作，那麼面對非奇異局勢，先拿者必勝；反之，則後拿者取勝。

5、練習：poj 1067

三、Fibonacci博弈

1、問題模型：

 有一堆個數為n的石子，遊戲雙方輪流取石子，滿足： 

（1）先手不能在第一次把所有的石子取完； 

（2）之後每次可以取的石子數介於1到對手剛取的石子數的2倍之間（包含1和對手剛取的石子數的2倍）。 約定取走最後一個石子的人為贏家。

2、解決思路：

  當n為Fibonacci數時，先手必敗。即存在先手的必敗態當且僅當石頭個數為Fibonacci數。 

    證明：根據“Zeckendorf定理”（齊肯多夫定理）：任何正整數可以表示為若干個不連續的Fibonacci數之和。如n=83 = 55+21+5+2，我們看看這個分解有什麼指導意義：假如先手取2顆，那麼後手無法取5顆或更多，而5是一個Fibonacci數，那麼一定是先手取走這5顆石子中的最後一顆，同理，接下去先手取走接下來的後21顆中的最後一顆，再取走後55顆中的最後一顆，那麼先手贏。

    反證：如果n是Fibonacci數，如n=89：記先手一開始所取的石子數為y

    （1）若y>=34顆（也就是89的向前兩項），那麼一定後手贏，因為89-34=55=34+21<2*34。

    （2）y<34時剩下的石子數x介於55到89之間，它一定不是一個Fibonacci數，把x分解成Fibonacci數：x=55+f[i]+…+f[j]，若，如果f[j]<=2y，那麼對B就是面臨x局面的先手，所以根據之前的分析，後手只要先取f[j]個即可，以後再按之前的分析就可保證必勝。

3、練習題目：NYOJ 取石子游戲

四、尼姆博弈

1、問題模型：有三堆各若干個物品，兩個人輪流從某一堆取任意多的物品，規定每次至少取一個，多者不限，最後取光者得勝。

2、解決思路：用（a，b，c）表示某種局勢，顯證（0，0，0）是第一種奇異局勢，無論誰面對奇異局勢，都必然失敗。第二種奇異局勢是（0，n，n），只要與對手拿走一樣多的物品，最後都將導致（0，0，0）。

  搞定這個問題需要把必敗態的規律找出：(a,b,c)是必敗態等價於a^b^c=0(^表示異或運算）。

  證明:(1)任何p(a,b,c)=0的局面出發的任意局面(a,b,c’);一定有p(a,b,c’)不等於0。否則可以得到c=c’。

      （2）任何p(a,b,c)不等於0的局面都可以走向 p(a,b,c)=0的局面

       (3）對於 (4,9,13) 這個容易驗證是奇異局勢

             

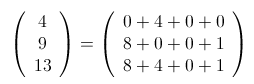
       其中有兩個8，兩個4，兩個1，非零項成對出現，這就是尼姆和為  零的本質。別人要是拿掉13裡的8或者1，那你就拿掉對應的9  中的那個8或者1；別人要是拿        掉13裡的4，你就拿掉4裡的4；  別人如果拿掉13裡的3，就把10作分解，然後想辦法滿 足非零項成對即可。

3、推廣一：如果我們面對的是一個非奇異局勢（a，b，c），要如何變為奇異局勢呢？假設 a < b< c,我們只要將 c 變為 a^b,即可,因為有如下的運算結果: a^b^(a^b)=(a^a)^(b^b)=0^0=0。要將c 變為a^b，只從 c中減去 c-（a^b）

4、推廣二：當石子堆數為n堆時，則推廣為當對每堆的數目進行亦或之後值為零是必敗態。

5、練習：hdoj 1847

五、公平組合博弈（Impartial Combinatori Games）

1、定義：

（1）兩人蔘與。

（2）遊戲局面的狀態集合是有限。

（3）對於同一個局面，兩個遊戲者的可操作集合完全相同

（4）遊戲者輪流進行遊戲。

（5）當無法進行操作時遊戲結束，此時不能進行操作的一方算輸。

（6）無論遊戲如何進行，總可以在有限步數之內結束。

2、模型：給定一個有向無環圖和一個起始頂點上的一枚棋子，兩名選手交替的將這枚棋子沿有向邊進行移動，無法移動者判負。事實上，這個遊戲可以認為是所有公平組合遊戲（Impartial Combinatori Games）的抽象模型。其實，任何一個ICG都可以通過把每個局勢看成一個頂點，對每個局勢和它的子局勢連一條有向邊來抽象成這個“有向圖遊戲”。

3、解決思路：

現在，假定我們給出兩個遊戲G1 和 G2。如果我們只知道單個遊戲的P-狀態和N-狀態我們能夠正確地玩好遊戲和G1 + G2嗎？答案是否定的。不難看出兩個P-狀態的和總是P-狀態，P-狀態和N-狀態的和總是N-狀態。但是兩個N-狀態的和既可能是P-狀態也可能是N-狀態。因此，只知道單個遊戲的P-狀態和N-狀態是不夠的。

為了正確地玩好遊戲和我們需要推廣P-狀態和N-狀態，它就是Sprague-Grudy函式（或者簡稱為g函式）

4、Sprague-Grudy定理：

令N = {0, 1, 2, 3, ...} 為自然數的集合。Sprague-Grundy 函式給遊戲中的每個狀態分配了一個自然數。結點v的Grundy值等於沒有在v的後繼的Grundy值中出現的最小自然數.

形式上：給定一個有限子集 S ⊂ N,令mex S(最小排斥值)為沒有出現在S中的最小自然數。定義mex(minimal excludant)運算，這是施加於一個集合的運算，表示最小的不屬於這個集合的非負整數。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

對於一個給定的有向無環圖，定義關於圖的每個頂點的Sprague-Garundy函式g如下：g(x)=mex{ g(y) | y是x的後繼 }。

5、性質：

（1）所有的終結點所對應的頂點，其SG值為0，因為它的後繼集合是空集——所有終結點是必敗點（P點）。

（2）對於一個g(x)=0的頂點x，它的所有後繼y都滿足g(y)!=0——無論如何操作，從必敗點（P點）都只能進入必勝點（N點）//對手走完又只能把N留給我們。

（3）對於一個g(x)!=0的頂點，必定存在一個後繼點y滿足g(y)=0——從任何必勝點（N點）操作，至少有一種方法可以進入必敗點（P點）//就是那種我們要走的方法。

6、應用：

（1）可選步數為1-m的連續整數，直接取模即可，SG(x) = x % (m+1); 

（2）可選步數為任意步，SG(x) = x; 

（3）可選步數為一系列不連續的數，用mex(計算每個節點的值) 

7、練習：hdoj 1847 1536 3980

SG函式