深入剖析迴歸（二）L1，L2正則項，梯度下降
一、迴歸問題的定義
迴歸是監督學習的一個重要問題，迴歸用於預測輸入變數和輸出變數之間的關係。迴歸模型是表示輸入變數到輸出變數之間對映的函式。迴歸問題的學習等價於函式擬合：使用一條函式曲線使其很好的擬合已知函式且很好的預測未知資料。 迴歸問題分為模型的學習和預測兩個過程。基於給定的訓練資料集構建一個模型，根據新的輸入資料預測相應的輸出。 迴歸問題按照輸入變數的個數可以分為一元迴歸和多元迴歸；按照輸入變數和輸出變數之間關係的型別，可以分為線性迴歸和非線性迴歸。 一元迴歸：y = ax + b
多元迴歸：
二、迴歸問題的求解
2.1解析解
2.1.1 最小二乘法
最小二乘法又稱最小平方法，它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料，並使得這些求得的資料與實際資料之間誤差的平方和為最小。最小二乘法還可用於曲線擬合。
2.1.2利用極大似然估計解釋最小二乘法
現在假設我們有m個樣本，我們假設有：
誤差項是IID，根據中心極限定理，由於誤差項是好多好多相互獨立的因素影響的綜合影響，我們有理由假設其服從高斯分佈，又由於可以自己適配theta0，是的誤差項的高斯分佈均值為0，所以我們有
所以我們有：
也即：
表示在theta給定的時候，給我一個x，就給你一個y
那麼我們可以寫出似然函式：
由極大似然估計的定義，我們需要L(theta)最大，那麼我們怎麼才能是的這個值最大呢？兩邊取對數對這個表示式進行化簡如下：
需要 l(theta)最大，也即最後一項的後半部分最小，也即： 目標函式（損失函式）
所以，我們最後由極大似然估計推導得出，我們希望 J(theta) 最小，而這剛好就是最小二乘法做的工作。而回過頭來我們發現，之所以最小二乘法有道理，是因為我們之前假設誤差項服從高斯分佈，假如我們假設它服從別的分佈，那麼最後的目標函式的形式也會相應變化。 好了，上邊我們得到了有極大似然估計或者最小二乘法，我們的模型求解需要最小化目標函式J(theta)，那麼我們的theta到底怎麼求解呢？有沒有一個解析式可以表示theta?
2.1.3 theta的解析式的求解過程
我們需要最小化目標函式，關心 theta 取什麼值的時候，目標函式取得最小值，而目標函式連續，那麼 theta 一定為 目標函式的駐點，所以我們求導尋找駐點。 求導可得：
最終我們得到引數 theta 的解析式：
上述最後一步有一些問題，假如 X'X不可逆呢？ 我們知道 X'X 是一個半正定矩陣，所以若X'X不可逆或為了防止過擬合，我們增加lambda擾動，得到
從另一個角度來看，這相當與給我們的線性迴歸引數增加一個懲罰因子，這是必要的，我們資料是有干擾的，不正則的話有可能資料對於訓練集擬合的特別好，但是對於新資料的預測誤差很大。
2.1.4正則化
L2-norm: （Ridge迴歸）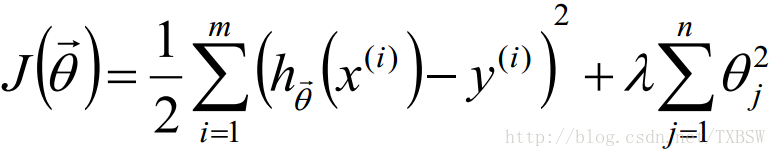
L1-norm: （Lasso迴歸）
L1-norm 和 L2-norm都能防止過擬合，一般L2-norm的效能更好一些。L1-norm能夠進行特選擇對資料進行降維 產生稀疏模型，能夠幫助我們去除某些特徵，因此可以用於特徵選擇。
Elastic Net：
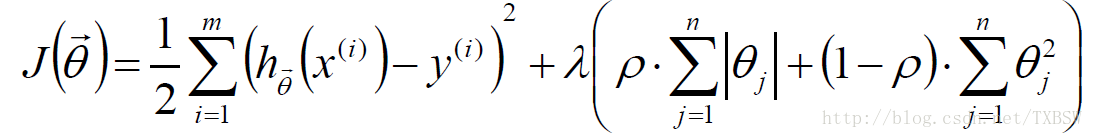
L1-norm 和 L2-norm都能防止過擬合，一般L2-norm的效果更好一些。L1-norm能夠產生稀疏模型，能夠幫助我們去除某些特徵，因此可以用於特徵選擇。
正則化（Regularization）
機器學習中幾乎都可以看到損失函式後面會新增一個額外項，常用的額外項一般有兩種，一般英文稱作ℓ1-norm和ℓ2-norm，中文稱作L1正則化和L2正則化，或者L1範數和L2範數。 L1正則化和L2正則化可以看做是損失函式的懲罰項。所謂『懲罰』是指對損失函式中的某些引數做一些限制。對於線性迴歸模型，使用L1正則化的模型建叫做Lasso迴歸，使用L2正則化的模型叫做Ridge迴歸（嶺迴歸）。下圖是Python中Lasso迴歸的損失函式，式中加號後面一項α||w||1即為L1正則化項。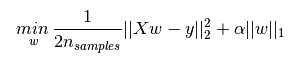
下圖是Python中Ridge迴歸的損失函式，式中加號後面一項α||w||22即為L2正則化項。
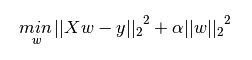一般迴歸分析中迴歸w表示特徵的係數，從上式可以看到正則化項是對係數做了處理（限制）。L1正則化和L2正則化的說明如下：
- L1正則化是指權值向量w中各個元素的絕對值之和，通常表示為||w||1
- L2正則化是指權值向量w中各個元素的平方和然後再求平方根（可以看到Ridge迴歸的L2正則化項有平方符號），通常表示為||w||2
- L1正則化可以產生稀疏權值矩陣，即產生一個稀疏模型，可以用於特徵選擇
- L2正則化可以防止模型過擬合（overfitting）；一定程度上，L1也可以防止過擬合
稀疏模型與特徵選擇
上面提到L1正則化有助於生成一個稀疏權值矩陣，進而可以用於特徵選擇。為什麼要生成一個稀疏矩陣？ 稀疏矩陣指的是很多元素為0，只有少數元素是非零值的矩陣，即得到的線性迴歸模型的大部分系數都是0. 通常機器學習中特徵數量很多，例如文字處理時，如果將一個片語（term）作為一個特徵，那麼特徵數量會達到上萬個（bigram）。在預測或分類時，那麼多特徵顯然難以選擇，但是如果代入這些特徵得到的模型是一個稀疏模型，表示只有少數特徵對這個模型有貢獻，絕大部分特徵是沒有貢獻的，或者貢獻微小（因為它們前面的係數是0或者是很小的值，即使去掉對模型也沒有什麼影響），此時我們就可以只關注係數是非零值的特徵。這就是稀疏模型與特徵選擇的關係。L1和L2正則化的直觀理解
這部分內容將解釋為什麼L1正則化可以產生稀疏模型（L1是怎麼讓係數等於零的），以及為什麼L2正則化可以防止過擬合。L1正則化和特徵選擇
假設有如下帶L1正則化的損失函式： J=J0+α∑w|w|(1) 其中J0是原始的損失函式，加號後面的一項是L1正則化項，α是正則化係數。注意到L1正則化是權值的絕對值之和，J是帶有絕對值符號的函式，因此J是不完全可微的。機器學習的任務就是要通過一些方法（比如梯度下降）求出損失函式的最小值。當我們在原始損失函式J0後新增L1正則化項時，相當於對J0做了一個約束。令L=α∑w|w|，則J=J0+L，此時我們的任務變成在L約束下求出J0取最小值的解。考慮二維的情況，即只有兩個權值w1和w2，此時L=|w1|+|w2|對於梯度下降法，求解J0的過程可以畫出等值線，同時L1正則化的函式L也可以在w1w2的二維平面上畫出來。如下圖：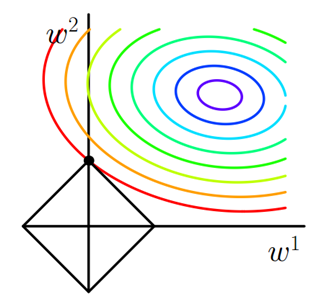
圖1 L1正則化
圖中等值線是J0的等值線，黑色方形是L函式的圖形。在圖中，當J0等值線與L圖形首次相交的地方就是最優解。上圖中J0與L在L的一個頂點處相交，這個頂點就是最優解。注意到這個頂點的值是(
相關推薦
深入剖析迴歸（二）L1，L2正則項，梯度下降
一、迴歸問題的定義 迴歸是監督學習的一個重要問題，迴歸用於預測輸入變數和輸出變數之間的關係。迴歸模型是表示輸入變數到輸出變數之間對映的函式。迴歸問題的學習等價於函式擬合：使用一條函式曲線使其很好的擬合已知函式且很好的預測未知資料。 迴歸問題分為模型的學習和預測兩個
為什麼L1正則項產生稀疏的權重，L2正則項產生相對平滑的權重
L1 和L2正則項的定義如下： L1=∑i|wi|L2=∑i(wi)2 L 1 =
l2-loss，l2範數，l2正則化，歐式距離
access src 梯度 com inf content 開平 nbsp alt 歐式距離： l2範數： l2正則化： l2-loss(也叫平方損失函數)： http://openaccess.thecvf.com/content_cvpr_2017/papers
L1、L2 正則項詳解 - 解空間、先驗分佈、最大似然估計 and 最大後驗估計
L1、L2 正則項詳解（解空間、先驗分佈） 引入 直觀看 解空間 先驗分佈 最大似然估計 最大後驗估計 引入 線上性迴歸
機器學習筆記（二）L1，L2正則化
2.正則化 2.1 什麼是正則化？ (截自李航《統計學習方法》) 常用的正則項有L1，L2等，這裡只介紹這兩種。 2.2 L1正則項 L1正則，又稱lasso，其公式為： L1=α∑kj=1|θj| 特點：約束θj的大小，並且可以產
Redis深入學習筆記（二）client list 命令詳解
學習 字節數組 height 要求 ddr idt 設置 分配 分組 Redis的client list 命令可以獲取當前連接到redis server端的所有客戶端以及相關狀態，本篇主要介紹每一個參數的作用。 clisnt list 命令輸出結果如下： （1）標識：id
學習之路（二）淺談：bash及其特性，命令歷史以及用戶管理及權限，shell的類型
bash 管理權限 過了一周了，進度似乎有點懈怠，不過過了周末重整旗鼓啦shell（外殼）GUI：Gnome，KDE，xfceCLI：sh，csh，ksh，bashbash（父進程）-----bash（子進程）他們相互獨立彼此不知命令歷史：historybash支持的引號：‘ ’命令替換（鍵盤~的按鍵
深入理解http（二）------http的緩存機制及原理
dad hl7 工作 tps sla vhk b+ vpp lrn 一、概念基礎 參考原文：https://blog.csdn.net/hiredme/article/details/73468040 http的緩存，主要存在於本地瀏覽器和web代理服務器中。 在
Python地理位置信息庫geopy的使用（二）：根據中心點坐標，方向，距離計算坐標
block 我們 code ram des int pri 經緯 kilo 上一篇文章我們介紹了geopy的基本使用，這一篇文章我們根據中心點坐標，方向，距中心點距離計算出對應的坐標點，這種用法官網並沒有給出詳細的文檔，我們這裏做一下說明 生成坐標點的具體方法 impor
深入理解Plasma（二）Plasma 細節
這一系列文章將圍繞以太坊的二層擴容框架，介紹其基本執行原理，具體操作細節，安全性討論以及未來研究方向等。本篇文章主要對 Plasma 一些關鍵操作的細節進行剖析。 在上一篇文章中我們已經理解了什麼是 Plasma 框架以及它是如何執行的，這一篇文章將對其執行過程中的一些關鍵部分，包括 Plasma 提交區塊
深入理解overlayfs（二）：使用與原理分析
在初步瞭解overlayfs用途之後，本文將介紹如何使用overlayfs以及理解該檔案系統所特有的一些功能特性。由於目前主線核心對overlayfs正在不斷的開發和完善中，因此不同的核心版本改動可能較大，本文儘量與最新的核心版本保持一致，但可能仍會存在細微的出入。 核心版本：Linux-4.1
成長記錄貼之springboot+shiro（二） {完成一個完整的許可權控制，詳細步驟}
近一個月比較忙，公司接了一個新專案，領導要求用shiro進行安全管理，而且全公司只有我一個java，從專案搭建到具體介面全是一個人再弄。不過剛好前段時間大概學習了一下shiro的使用，還算順利。 &n
Android 如何從應用深入到Framework （二）
分享轉發，舉手之勞，手有餘香。 Android 如何從應用深入到Framework （一） 上節講到了孵化器，講到了system server程序，同時說了system server的一堆執行緒，比如我們熟悉的AMS WMS PMS ，這幾個服務執行緒，完成應
【機器學習】softmax迴歸（二）
通過上篇softmax迴歸已經知道大概了，但是有個缺點，現在來仔細看看 Softmax迴歸模型引數化的特點 Softmax 迴歸有一個不尋常的特點：它有一個“冗餘”的引數集。為了便於闡述這一特點，假設我們從引數向量 中減去了向量 ，這時，每一個
Python基礎（二）--- IDEA中整合Python和MySQL，使用Python進行SQL操作
一、Python操作MySQL ----------------------------------------------------- 1.安裝MySQL 2.安裝mysql的python模組 a.下載並安裝PyMySQL-master.zip
線性迴歸（二）
本文參考： 1)崔家華：https://cuijiahua.com/blog/2017/12/ml_12_regression_2.html 2)zsffuture: https://blog.csdn.net/weixin_42398658/article/details/835
解析ArcGis的欄位計算器（二）——有玄機的要素Geometry屬性，在屬性表就能查出孔洞、多部件
ArcGis裡多部件要素一般有兩種，一種是孔洞、一種是Merge在一起的兩個面。有時候為了便於賦屬性或者其他的一些原因，我們在操作中會故意Merge一些本不在一起的面，造成上述的第二種情況。藉助欄位計算器可以在屬性表中直接把它們標識出來，信不？注：以下語句需要使用Python解析。先上!shape.isMul
深入資料庫事務（二）事務的隔離級別
深入資料庫事務（二）事務的隔離級別 本文詳細介紹四種事務隔離級別，並通過舉例的方式說明不同的級別能解決什麼樣的讀現象。並且介紹了在關係型資料庫中不同的隔離級別的實現原理。 在DBMS中，事務保證了一個操作序列可以全部都執行或者全部都不執行（原子性），從一個狀態轉變到
深入剖析tomcat（一）
伺服器端建立serverSocket物件，監聽指定ip、指定埠的請求 客戶端建立socket物件（指定需要請求的伺服器端的ip和埠），發出請求 伺服器端接收到客戶端的請求，建立與之相對應的socket物件，連結建立。serverSocket繼續監聽其他請求 客戶端通過socket的getOutputSt
深入理解JVM（二）——記憶體模型、可見性、指令重排序
記憶體模型 首先我們思考一下一個java執行緒要向另外一個執行緒進行通訊，應該怎麼做，我們再把需求明確一點，一個java執行緒對一個變數的更新怎麼通知到另外一個執行緒呢？我們知道java當中的例項物件、陣列元素都放在java堆中，java堆是執行緒共享的。（我們這裡