【Java程式設計的邏輯】堆與優先順序佇列&PriorityQueue
完全二叉樹 & 滿二叉樹 & 堆
基本概念
滿二叉樹是指除了最後一層外,每個節點都有兩個孩子,而最後一層都是葉子節點,都沒有孩子。
滿二叉樹一定是完全二叉樹,但完全二叉樹不要求最後一層是滿的,但如果不滿,則要求所有節點必須集中在最左邊,從左到右是連續的,中間不能有空的。
特點
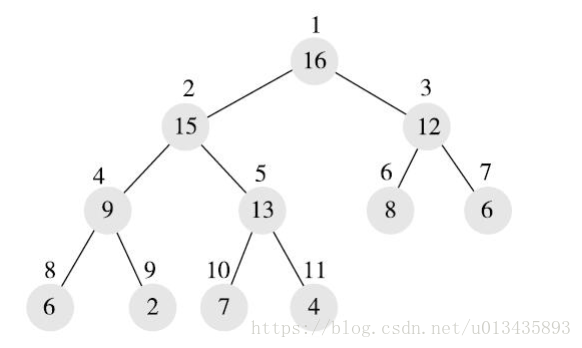
在完全二叉樹中,可以給每個節點一個編號,編號從1開始連續遞增,從上到下,從左到右
完全二叉樹有一個重要的特點:給定任意一個節點,可以根據其編號直接快速計算出其父節點和孩子節點。如果編號為i,則父節點編號為i/2,左孩子編號為2*i,右孩子編號為2*i+1
它使得邏輯概念上的二叉樹可以方便地儲存到陣列中,陣列中的元素索引就對應節點的編號,樹中的父子關係通過其索引關係隱含維持,不需要單獨保持。
這種儲存二叉樹的方法與之前介紹的TreeMap是不一樣的。在TreeMap中,有一個單獨的內部類Entry,Entry有三個引用,分別指向父節點、左孩子、右孩子。使用陣列儲存的優點是節省空間,而且訪問效率高。
堆
堆邏輯概念上是一棵完全二叉樹,而物理儲存上使用陣列,還要一定的順序要求。
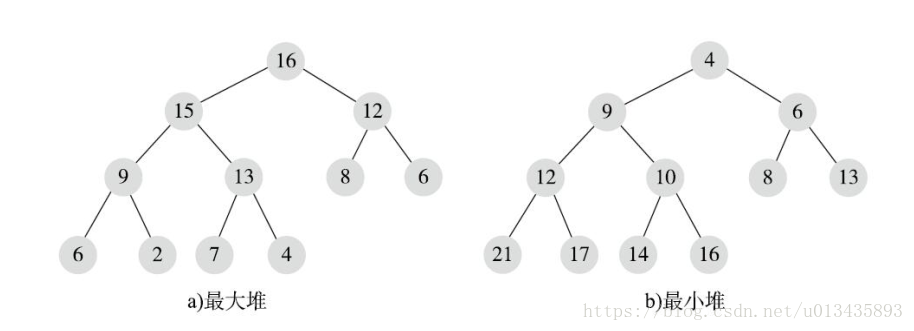
TreeMap內部使用的是排序二叉樹原理,排序二叉樹是完全有序的,每個節點都有確定的前驅和後繼,而且不能有重複元素。與排序二叉樹不同,在堆中,可以有重複元素,元素間不是完全有序的,但對於父子節點直接,有一定的順序要求。根據順序分為兩種堆:最大堆、最小堆
最大堆是指每個節點都不大於其父節點。這樣,對於每個父節點,一定不小於其所有孩子節點,那麼根節點就是所有節點中最大的了。最小堆與最大堆就正好相反,每個節點都不小於其父節點。
總結來說:堆是完全二叉樹,父子節點間有特定順序,分為最大堆和最小堆,堆使用陣列進行物理儲存。
堆的操作
新增元素
這裡我們以最小堆為例進行講解
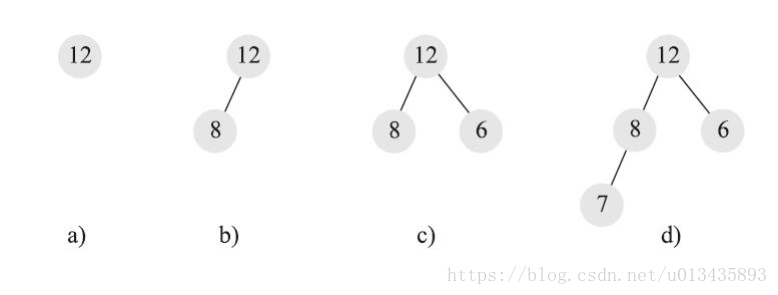
如果堆為空,則直接新增一個根就行了。
如果堆不為空,要在其中新增元素,基本步驟為:
1. 新增元素到最後位置
2. 與父節點比較,如果大於等於父節點,則滿足堆的性質,結束。否則與父節點進行交換,然後再與父節點比較和交換,直到父節點為空或者大於等於父節點。
該方法稱為向上調整
新增一個元素,需要比較和交換的次數最多為樹的高度,即log(N)。N為節點數
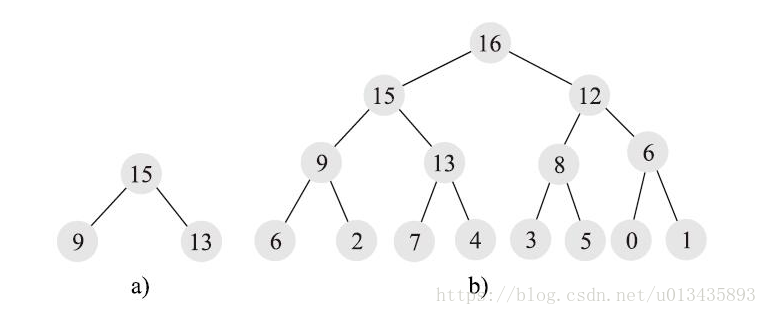
從頭部刪除元素
- 用最後一個元素替換頭部元素,並刪掉最後一個元素
- 將新的頭部與兩個孩子節點中較小的比較,如果不大於該孩子節點,則滿足堆的性質,結束。否則與較小的孩子節點進行交換,交換後,再與較小的孩子節點比較,一直到沒有孩子節點或者不大於兩個孩子節點。
該方法稱為向下調整
從中間刪除元素
- 與從頭部刪除一樣,先用最後一個元素替換待刪元素。
- 有兩種情況,如果該元素大於某孩子節點,則需要向下調整;如果小於父節點,則需要向上調整。
查詢和遍歷
在堆中進行查詢沒有特殊的演算法,就是從陣列的頭找到尾,效率為O(N)
在堆中進行遍歷也是類似的。
構建堆
給定一個無序陣列,如何使之成為一個最小堆呢?
基本思路是:從最後一個非葉子節點開始,一直往前直到根,對每個節點,執行向下調整。換句話說,自底向上。先使每個最小子樹為堆,然後對左右子樹和其父節點合併,調整為更大的堆,因為每個子樹已經為堆,所以調整就是堆父節點執行向下調整,這樣一直合併調整到根。
小結
- 在新增和刪除元素時,效率為O(logN)
- 查詢和遍歷元素,效率為O(N)
- 構建堆的效率是O(N)
PriorityQueue
PriorityQueue是優先順序佇列,實現了佇列介面(Queue),內部是用堆實現的,內部元素不是完全有序的,不過,逐個出對會得到有序的輸出。
基本用法
PriorityQueue有多個構造方法:
public PriorityQueue();
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator);
public PriorityQueue(Collection<? extends E> c);PriorityQueue是用堆實現的,堆物理上就是陣列,與ArrayList類似,都是使用動態資料,根據元素的個數進行動態擴充套件,initialCapacity表示初始化的陣列大小,預設為11。與TreeMap/TreeSet類似,為了保持一定順序,PriorityQueue要求要麼元素實現Comparable介面,要麼傳遞一個比較器Comparator。
實現原理
先看看內部組成成員:
// 實際儲存元素的陣列
private transient Object[] queue;
// 當前元素個數
private int size = 0;
// 比較器,可以為null
private final Comparator<? super E> comparator;
// 修改次數
private transient int modCount = 0;構造方法上面已經提到過了,主要是初始化queue和comparator 。 操作相關的程式碼和上面的堆的操作差不多的,這裡我們以入隊為例,做一個簡單的講解
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
// 確保陣列長度是夠的
if (i >= queue.length)
grow(i + 1);
// 元素長度增加
size = i + 1;
// 如果第一次新增,直接放在第一個位置
if (i == 0)
queue[0] = e;
// 否則將其放入最後一個位置,並向上調整
else
siftUp(i, e);
return true;
}
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
// 如果原來長度比較小,擴充套件為兩倍,否則就增加50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
/**
* 向上調整
*/
private void siftUp(int k, E x) {
// 如果有比較器就用比較器
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
/**
* 向上尋找x真正應該插入的位置
* @param k 表示插入的位置
* @param x 表示新元素
*/
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
// 父節點位置,當前節點位置/2
int parent = (k - 1) >>> 1;
// 父節點
Object e = queue[parent];
// 如果新元素大於等於父節點,則滿足堆的性質,退出
if (comparator.compare(x, (E) e) >= 0)
break;
// 否則父元素下移,繼續向上尋找
queue[k] = e;
k = parent;
}
queue[k] = x;
}小結
- 實現了優先順序佇列,最先出對的總是優先順序最高的
- 優先順序可以有相同的,內部元素不是完全有序的
- 檢視頭部元素效率很高為O(1),入隊、出隊效率較高為O(logN),構建堆的效率為O(N)
- 查詢和刪除的效率比較低為O(N)
堆和PriorityQueue的應用
問題
這裡先丟擲兩個比較常見的問題,然後再用堆的思想來進行解決
1. 求前K個最大的元素,元素個數不確定,資料量可能很大,甚至源源不斷到來,但需要知道目前為止最大的前K個元素
2. 求中值元素,中值不是平均值,而是排序後中間那個元素的值,同樣資料量可能很大,甚至源源不斷到來
求前K個最大的元素
一個簡單的思路是排序,排序後取最大的K個就可以了,排序可以使用Arrays.sort()方法,效率為O(N*log(N))。Arrays.sort()使用的是經過調優的快速排序法 。
另一種思路是選擇,迴圈選擇K次,每次從剩下的元素中選擇最大值,效率為O(N*K),如果K值大於log(N),就不如排序了。
不過這兩個思路都是假定所有元素都是已知的,而不是動態的。如果元素個數不確定,且源源不斷到來呢?
一個基本的思路是維護一個長度為K的陣列,最前面的K個元素就是目前最大的K個元素,以後每來一個新元素的時候,都先找到陣列中最小值,將新元素與最小值相比,如果小於最小值,什麼都不用做;如果大於最小值,則將最小值替換為新元素。
這類似於生活中常見的末尾淘汰。
這樣,陣列中維護的永遠都是最大的K個元素,不管資料來源有多少,需要的記憶體開銷是固定的,就是長度為K的陣列。不過,每來一個元素,都需要找最小值,都需要進行K次比較,能不能減少比較次數呢?
解決方法是使用最小堆維護這個K個元素,最小堆中,根即第一個元素永遠都是最小的,新來的元素與根比較就可以了,如果小於根,則堆不需要變化,否則用新元素替換根,然後向下調整堆即可,調整的效率為O(logK),總體效率就是O(N*logK)。而且使用了最小堆後,第K個最大的元素也很容易獲取,它就是堆的根
public class TopK<E> {
private PriorityQueue<E> p;
private int k;
public TopK(int k) {
this.k = k;
this.p = new PriorityQueue<>(k);
}
public void addAll(Collection<? extends E> c) {
for(E e: c) {
add(e);
}
}
public void add(E e) {
if(p.size() < k) {
p.add(e);
return ;
}
Comparable<? super E> head = (Comparable<? super E>)p.peek();
if(head.compareTo(e)>0) {
// 小於TopK中的最小值,不用變
return ;
}
// 新元素替換掉原來最小值成為TopK之一
p.poll();
p.add(e);
}
public <T> T[] toArray(T[] a) {
return p.toArray(a);
}
public E getKth() {
return p.peek();
}
}求中值
中值就是排序後中間那個元素的值,如果元素個數為奇數,中值是沒有歧義的,如果是偶數,可以為偏小的,也可以為偏大的。
一個簡單的思路就是排序,排序後取中間的那個值就可以了。排序可以使用Arrays.sort()方法,效率為O(N*log(N))。
當然,這是要在資料來源已知的情況下才能做到的。如果資料來源源不斷到來呢?
可以使用兩個堆,一個最大堆,一個最小堆
1. 假設當前的中位數為m,最大堆維護的是<=m的元素,最小堆維護的是>=m的元素,但兩個堆都不包含m。
2. 當新的元素到達時,比如為e,將e與m進行比較,若e<=m,則將其加入最大堆中,否則加入最小堆中
3. 如果此時最小堆和最大堆的元素個數相差>=2,則將m加入元素個數少的堆中,然後從元素個數多的堆將根節點移除並賦值給m。
給個示例解釋一下,輸入的元素依次是:34,90,67,45,1
1. 輸入第一個元素時,m賦值為34
2. 輸入第二個元素時,90>34,把90加入最小堆,m不變
3. 輸入第三個元素時,67>34,把67加入最小堆,此時最小堆根節點為67。但是現在最小堆中元素個數為2,最大堆中元素個數為0,所以需要做調整,把m(34)加入個數少的堆中(最大堆),然後從元素個數多的堆(最小堆)將根節點移除並賦值給m,所以現在m為67,最大堆中有34,最小堆中有90
4. 輸入第四個元素時,45<67,把45加入最大堆,m不變
5. 輸入第五個元素時,1<67,把1加入最大堆中,此時m為67,最大堆中有1,34,45,最小堆中有90,所以需要調整。調整後,m為45,最大堆為1,34,最小堆為67,90。
public class Median<E> {
// 最小堆
private PriorityQueue<E> minP;
// 最大堆
private PriorityQueue<E> maxP;
// 中值
private E m;
public Median() {
this.minP = new PriorityQueue<>();
this.maxP = new PriorityQueue<>(11, Collections.reverseOrder());
}
// 比較
private int compare(E e, E m) {
Comparable<? super E> cmpr = (Comparable<? super E>)e;
return cmpr.compareTo(e);
}
public void add(E e) {
if(m == null) {
// 第一個元素
m = e;
return ;
}
if(compare(e, m) < 0) {
// 如果e小於m,則加入最大堆
maxP.add(e);
} else {
// 如果e大於m,則加入最小堆
minP.add(e);
}
if(minP.size() - maxP.size() >= 2) {
// 最小堆中元素比最大堆中元素多2個
// 將m加入最大堆中,然後將最小堆中的根移除賦值給m
maxP.add(this.m);
this.m = minP.poll();
} else if(maxP.size() - minP.size() >= 2) {
minP.add(this.m);
this.m = maxP.poll();
}
}
public void addAll(Collection<? extends E> c) {
for(E e : c) {
add(e);
}
}
public E getM() {
return m;
}
}