順序儲存定義

線性表的順序儲存結構，指的是用一段地址連續的儲存單元依次儲存線性表的資料元素。

順序儲存方式

      線性表的順序儲存結構，就是在記憶體中找了塊地兒，通過站位的形式，把一定記憶體空間給佔了，然後把相同資料型別的資料元素依次存放到這塊空地中【可通過C中的一維陣列來實現順序儲存結構】。

描述順序儲存結構需要三個屬性：
1. 儲存空間的起始位置：陣列 data , 它的儲存位置就是儲存空間的儲存位置
2. 線性表的最大儲存容量
3. 線性表的當前長度

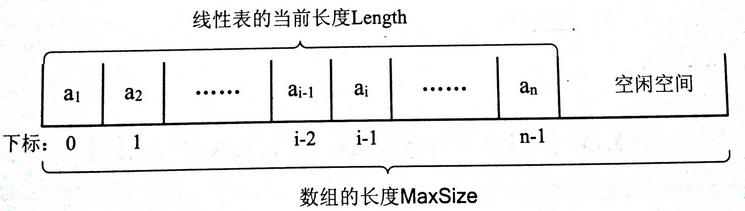
陣列長度 與 線性表長度區別
- 陣列長度：
即存放線性表的儲存空間的長度，儲存分配後這個量一般是不變的。

• 線性表長度：
  即線性表中資料元素的個數

在任意時刻，線性表的長度應該小於等於陣列的長度。

地址計算方法

      線性表是從1開始的，而陣列的下標是從0開始的，因此 線性表的第 i 個元素是要儲存在陣列下標為 i - 1 的位置，即資料元素的序號和存放它的陣列下標之間存在對應關係。

儲存器中的每個儲存單元都有自己的編號，這個編號稱為地址。

• 假設每個資料元素佔用的是 c 個 儲存單元，那麼線性表中第 i + 1 個數據元素的儲存位置和第 i 個數據元素的儲存位置滿足關係 ： LOC ( ai+1 ) = LOC ( ai ) + c ;
• 第 i 個數據元素 ai 的儲存位置： LOC ( ai ) = LOC ( a1 ) + （i - 1） c*

由上式公式得出結論：

1. 通過上面公式可隨時算出線性表中任意位置的地址，不管它是第一個還是最後一個，都是相同的時間。
2. 那麼對每個線性表位置的存取資料，對於計算機來說都是相等時間，即是一個常數，即存取時間效能為 O(1).

3. 把具有以上特點的儲存結構稱為隨機儲存結構

   順序儲存結構的插入與刪除

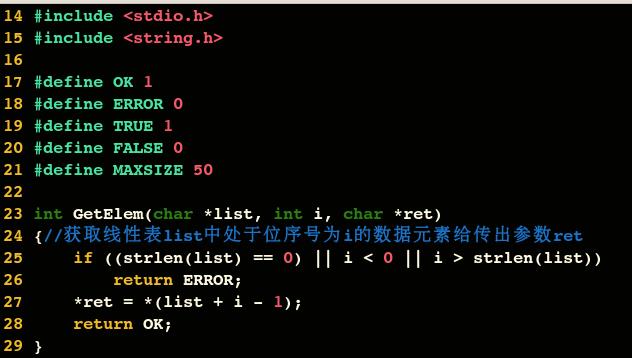
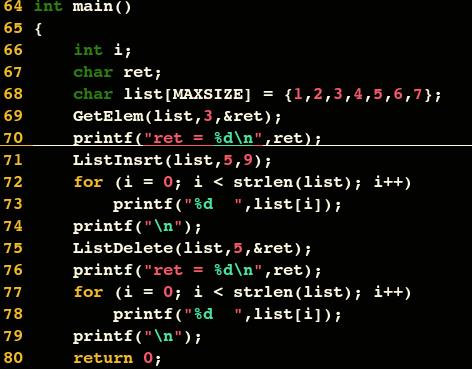
獲得元素操作

 對於線性表的順序儲存結構來說，要實現獲得元素操作，即將線性表 L 中的第 i 個位置元素值返回。

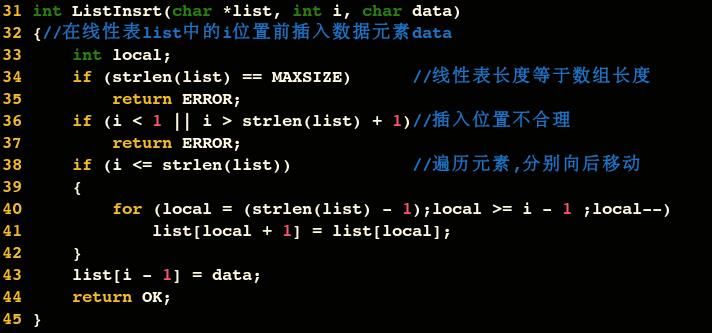
插入操作

插入演算法的思路：

1. 如果插入位置不合理，丟擲異常
2. 如果線性表長度大於等於陣列長度，則丟擲異常或動態增加容量
3. 從最後一個元素開始向前遍歷到第 i 個位置，分別將它們都向後移動一個位置
4. 將要插入元素填入位置 i 處
5. 表長加1

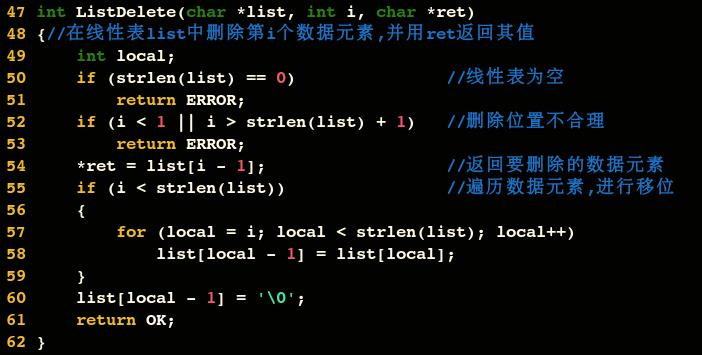
刪除操作

刪除演算法的思路：

1. 如果刪除位置不合理，丟擲異常
2. 取出刪除元素
3. 從刪除元素位置開始遍歷到最後一個元素位置，分別將它們都向前移動一個位置
4. 表長減1

分析插入和刪除的時間複雜度：

最好的情況：插入或刪除的都是最後一個元素，時間複雜度 O（1）
最壞的情況：插入或刪除的都是第一個元素，則所有其他元素都要進行移動，時間複雜度 O(n)
平均的情況：插入或刪除第 i 個元素，需要移動 n - i 個元素，時間複雜度 O(n)

結論：
線性表的順序儲存結構，在存、取資料時，不管是哪個位置，時間複雜度都是O(1)，而插入和刪除時，時間複雜度都是 O(n)。
適合元素個數不太變化，而更多是儲存資料的應用。