堆

堆在優先順序佇列的各種實現中，是最高效的一種資料結構
假定在各個資料記錄（或元素）中存在一個能夠標識資料記錄（或元素）的資料項，並將依據該資料項對資料進行組織，則可資料項成為關鍵碼（key）
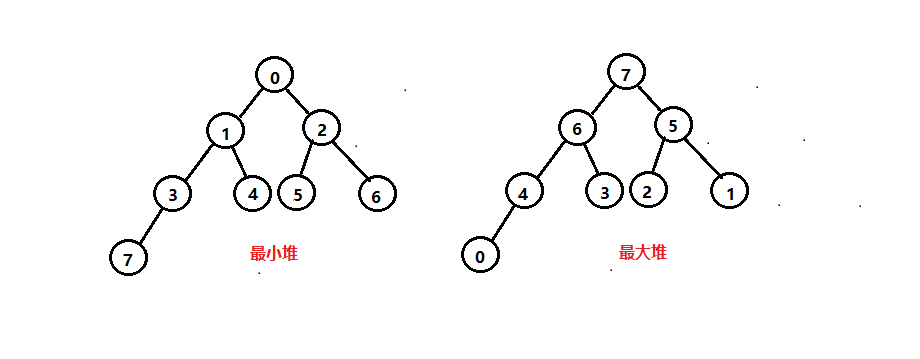
如果有一個關鍵碼的集合K = {k0 , k1 , k2 , … , kn-1},把它的所有元素按完全二叉樹的順序儲存存放在一個一維陣列中。並且滿足：

由於堆儲存在下標從0開始計數的陣列中，因此，在堆中給定下標為i的結點時：

1. 如果 i = 0，結點 i 是根結點，無父結點；否則結點 i 的父結點為結點 [(i - 2) / 2]
2. 如果 2i + 1 > n - 1，則結點 i 無左子女；否則結點 i 的左子女為結點 2i + 1
3. 如果 2i + 2 > n - 1，則結點 i 無右結點；否則結點 i 的右子女為結點 2i + 2

實現最小堆

第一步：建堆
利用給定的陣列大小和陣列元素，建立堆空間，並進行拷貝。
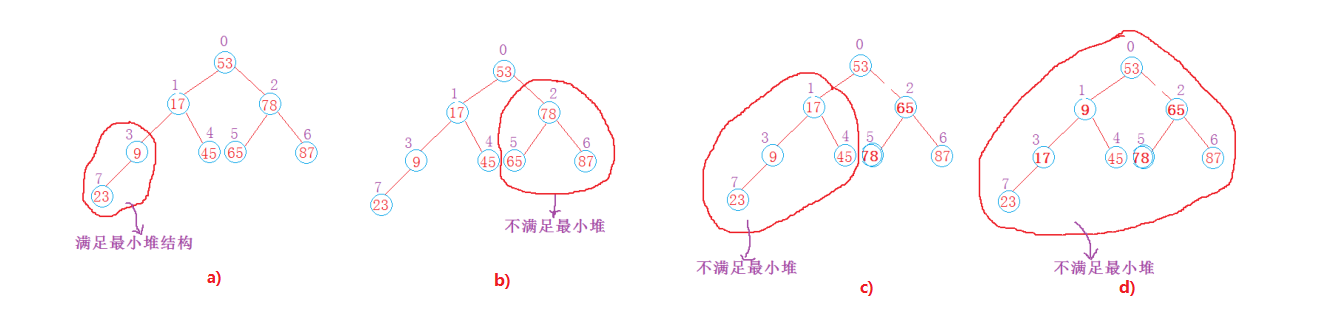
第二步：調整成為最小堆
利用自定義的siftDown()函式，實現下滑調整。

插入與刪除

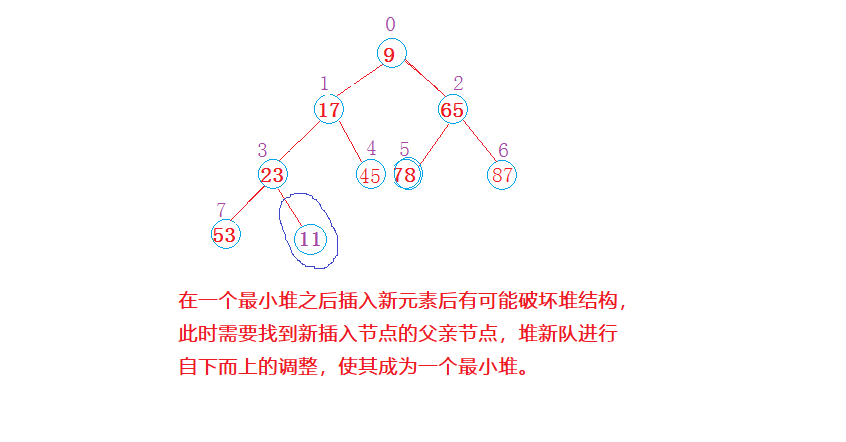
插入

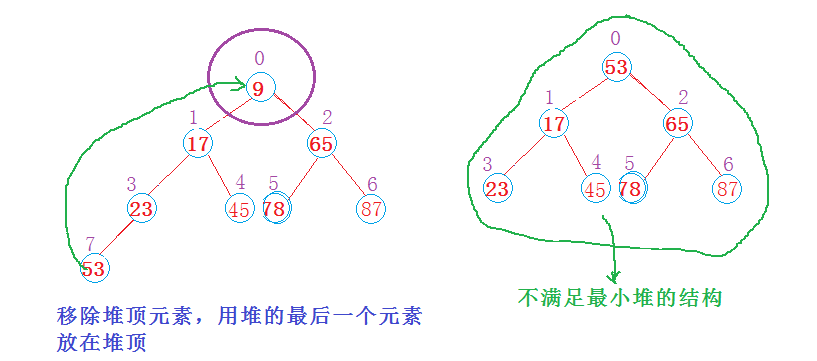
刪除
由於堆是佇列結構，只能從堆中刪除堆頂元素。移除堆頂元素之後，用堆的最後一個節點填補取走的堆頂元素，並將堆的實際元素個數減1。但用最後一個元素取代堆頂元素之後有可能破壞堆，因此需要將對自頂向下調整，使其滿足最大或最小堆。

#include<iostream>
using namespace std;


template<class T>
class Heap
{
public:
    //建構函式
    Heap()
    :haep(NULL)
    {}

    //建構函式
    Heap(T * arr, int sz)
    {
        HeapSize = (DefaultSize < sz) ? sz : DefaultSize;
        heap = new T[HeapSize];
        heap = arr;
        if
 
 (heap == NULL)
            cout << "記憶體分配失敗！" << endl;
        for (int i = 0; i < sz; i++)
            heap[i] = arr[i];
        currentSize = sz;
    }

    //調整為小堆
    void MinHeap()
    {
        currentPos = (currentSize - 2) / 2;//最初調整位置：最後分支點
        while (currentPos >= 0)
        {
            siftDown(currentPos, currentSize-1);
            currentPos--;
        }

    }

    //向堆插入新元素
    bool Insert(T x)
    {
        if (currentSize == HeapSize)
        {
            cerr << "Heap Full" << endl;
            return false;
        }

        heap[currentSize] = x;
        siftUp(currentSize);
        currentSize++;
        return true;

    }

private:
    T * heap;//存放堆的陣列
    int DefaultSize = 10;//預設堆的大小
    int HeapSize;//當前堆的大小
    int currentSize;//最小堆中當前元素個數
    int currentPos;//最初調整位置

    //從start到m下滑調整成為最小堆
    void siftDown(int start, int m)
    {
        int i = start;
        int j = 2 * i + 1;
        T temp = heap[i];
        while (j <= m)
        {
            if (j < m && heap[j] > heap[j + 1])
                j = j + 1;

            if (temp <= heap[j])
                break;
            else
            {
                heap[i] = heap[j];
                i = j;
                j = 2 * j + 1;
            }   
        }
        heap[i] = temp;
    }

    //從start到0上滑調整成為最小堆
    void siftUp(int start)
    {
        int j = start;
        int i = (start - 1) / 2;
        T temp = heap[j];
        while (j > 0)
        {           
            if (heap[i] >= temp)
            {
                heap[j] = heap[i];
                j = i;
                i = (i - 1) / 2;
            }
        }
        heap[j] = temp;
    }
};



int main()
{
    int arr[6] = { 5, 4, 3, 2, 1, 0 };
    Heap<int> s(arr, 6);
    s.MinHeap();
    s.Insert(-1);
    for (int i = 0; i < 6; i++)
        cout << arr[i] << " ";
    return 0;


}