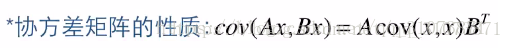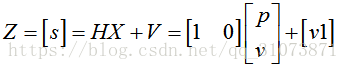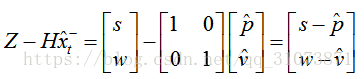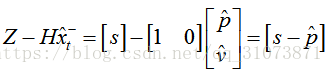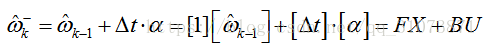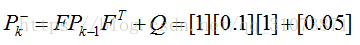一般我們程式設計中，常用的數學模型都是離散的，首先看一下離散的狀態空間表示式：

上面這張表格來自百度百科“狀態空間”

下面看一個實際問題：《卡爾曼濾波器的原理以及在matlab中的實現》

https://www.bilibili.com/video/av10788247?from=search&seid=10382691491488446111

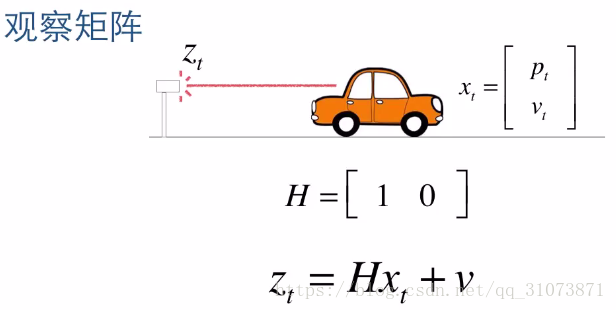
問題描述：一輛小車，我們可以任意控制它的加速度u(t)，要求實時輸出它的路程p(t)。

上面圖中推匯出的公式，就是卡爾曼狀態預測公式，式中的F矩陣稱為狀態轉移矩陣，B矩陣叫做控制矩陣。另外，①變數上面戴帽子，指的是該變數是個預測值，不是真實值，②左側的x帽右上角還帶減號，減號的意義是，這個x帽還不是最終的預測值，待會我們還要繼續修正他。

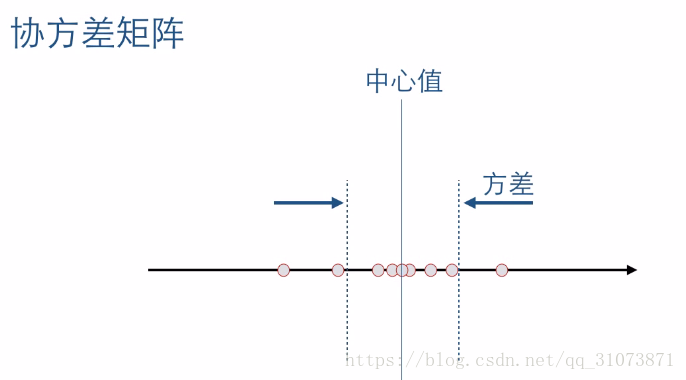
下面再來看一下協方差矩陣的直觀解釋，我們從一維資料開始逐步理解他：

上圖中的圓點為一些樣本資料，它們是帶有高斯噪聲的，於是這些樣本就表現為：圍繞在中心值附近，離散程度用方差來表示。換句話說，一維資料的協方差就是方差。那麼二維資料的協方差從直觀上怎麼理解呢？看下圖：

一組二維樣本，例如(2,1)、（2.3, 4）、(3, 4.5)·····，如何描述這組樣本的分佈情況呢？一個直觀的想法是，向上圖中的圖1一樣，把這組二維樣本分別投影到X/Y軸，這樣就得到了兩組一維的樣本，這樣每一組樣本都能獲得中心值和方差兩個引數了，但是這種思路只能描述二維資料的兩個維度相互獨立的情況，如果說，這兩個維度的資料不是相互獨立的（例如，當第一維的資料的噪聲為正值時，第二維的資料的噪聲也大概率為正值），這種情況下我們就不能用兩個一維的方差來描述二維樣本的分佈情況了，而必須把兩者的相關性也考慮進來。下面再看一下協方差矩陣的數學定義：

仔細觀察上述定義式，可知：如果兩個變數的變化趨勢一致，也就是說如果其中一個大於自身的期望值時另外一個也大於自身的期望值，那麼兩個變數之間的協方差就是正值；如果兩個變數的變化趨勢相反，即其中一個變數大於自身的期望值時另外一個卻小於自身的期望值，那麼兩個變數之間的協方差就是負值。

我們還發現，Cov(X,X)的公式其實就是單變數方差的公式：

對於兩個隨機變數X、Y的協方差矩陣就有4個元素：Cov(X,X)、Cov(X,Y)、Cov(Y,Y)、Cov(Y,X)，，顯然，主對角線上兩個元素分別是X、Y的方差Cov(X,X)和Cov(Y,Y)，反對角線上兩個元素的值是相等的->Cov(X,Y)=Cov(Y,X)。

上圖中，H稱為觀測矩陣（其實就是狀態空間表示式中的“輸出矩陣C”），z為測量值（例如，鐳射測距的值），v為測量誤差。如果我們能從小車外部測量到多個引數，例如我們能測到小車的路程s和實時速度w，那麼測量值Z就不再是一個標量值了，而變為一個列向量：

如果只能測到路程s，那麼上式就簡化為：

由此可見，觀測矩陣（輸出矩陣）的物理意義就是：根據狀態向量的值（這個值可能是測量值，也可能是數學模型算出的先驗估計值），輸出我們想要的變數的值。

前文中，我們提到，預測模型給出的預測值，並不是一個最優值，我們需要對它進行修正，修正方法如下：

上式中，即前文提到的數學模型給出的預測值，為測量值和數學模型預測值的差值，Kt為卡爾曼增益。

這個差值也有可能是個矩陣，這跟測量值的個數有關，如果測量值Z是列向量，那麼，該差值展開後即為：

如果只能測量距離s，那麼上式就退化為：

上面幾個式子中，
P為狀態協方差矩陣，其意義是，我們的先驗估計到底有多大的“不可信度”；

Q為狀態轉移協方差矩陣，其意義是，矩陣F到底有多大的“不可信度”；
H為觀測矩陣，其功能是把幾個狀態變數線性疊加為輸出變數，矩陣的值就是疊加所用的係數；

F為狀態轉移矩陣；
R為觀測噪聲的協方差矩陣，其意義是，我們的測量值到底有多大的“不可信度”；

P矩陣的初始值根據經驗/歷史樣本隨便設定一個差不多的值即可，別太誇張就行，該矩陣會自己迭代為合適的值，例如我們設定的P過大（傾向於不相信預測模型），結果在迭代中發現，預測的值還是挺準的，那麼第5式就會自動把P給減小（傾向於相信預測模型）

卡爾曼增益K的物理意義，其實很簡單，就一句話：你是更相信測量值，還是更相信先驗估計值，這個K就代表了你對測量值的信任程度。對測量值和先驗估計值的信任程度的比例K是如何求的？那就是第3式的工作了，第3式根據測量值的誤差協方差R和先驗估計值的協方差P-的大小，來決定K的大小，顯然，測量值的誤差協方差R越小，計算出的K值越大。

定量的來看一下極端情況，假設我們完全相信先驗估計，也即R=0矩陣，那麼K的計算結果就是,這個結果代入第4式，才可以把觀測值的尺度變換為狀態變數的尺度。

關於狀態轉移協方差矩陣Q，我們這樣來理解它：狀態向量X有兩個元素，路程p和速度v，我們用數學模型預測遞推求解新的狀態向量時，是這樣求解的：，在很多時候，我們建立的數學模型和實際的物理系統總是存在差異，例如我們用二階系統來描述電機，實際上如果考慮到電機的種種細節的話，二階方程是不足以描述電機的，再以路程預測為例，即使小車是勻加速運動，我們有標準的勻加速運動求解路程的公式，那麼這個公式就能完全吻合小車實際的位移嗎？顯然不可能，路面打滑、路面有坑、小車輪胎磨損等，都會使得我們的公式無法完全吻合實際的小車，無法完全吻合，這個問題就體現在轉移矩陣F並沒有描述到所有的細節，，p(t)是用p(t-1)和v(t-1)來預測的，他們的係數分別是1和Δt，這兩個係數的細節度不夠，從而造成預測誤差，那麼我們對p(t)的預測誤差，這個誤差具體是出在p(t-1)的係數1上呢？還是出在v(t-1)的係數Δt上呢？還是這兩個係數都有份呢？為了區分各個狀態變數的係數對下一週期狀態變數預測造成的誤差的不同程度，我們需要為每一個係數都描述一下它對造成預測誤差所做的“貢獻”，顯然，為了描述每一個係數，我們需要一個和係數矩陣一樣大的矩陣，這個矩陣就是狀態轉移協方差矩陣Q，假設Q取值為：，其物理意義就是，係數1和Δt對預測p(t)造成的誤差的貢獻分別為0.01、0.005，係數0和係數1對預測v(t)造成的誤差的貢獻分別為0.05、0.02，再說個題外話，如果兩個狀態變數X、Y完全不相關，也就是說，Y(t-1)的係數對預測X(t)不會產生任何影響，即使預測X(t)產生了誤差，那也是X(t-1)的係數不準確造成的，跟Y(t-1)的係數的無關，這種情況下，Q矩陣就會表現為反對角線的值都為0，也即X和Y的協方差為0。

下面我們把卡爾曼濾波用在“角度感測器和角加速度感測器，獲取真實角度”這個問題中，問題描述：在一個物體上安裝了一個角度感測器和一個角加速度感測器，角度感測器的特性是物體動作較慢時，測量很準確，但物體動作較快時，讀取出的測量結果帶有很大的噪聲，但均值基本是對的，而角加速度感測器，在物體動作很快時，仍可以準確的測量出角加速度，但是因為控制器只能以一定的時間間隔週期性的讀取角加速度，所以，無法求角加速度的積分，也就無法用角加速度的積分來求角度了，只能用Σ(αxΔt)來近似代替積分從而計算出角度，顯然這種近似會隨著時間的推移，累計誤差越來越大。實際上這個問題用互補濾波就可以簡單粗暴的解決，但這裡為了學習卡爾曼，我們用卡爾曼濾波來解決下這個問題。

先定義幾個變數：角速度為ω，角加速度為α，角度為a，所有變數的預測值都用帽子表示，

按照卡爾曼的標準五步來做：

（1）建立角度的預測模型（這是一個：非時變的離散的狀態空間模型）

F為狀態轉移矩陣，B為控制矩陣，X為狀態，U為輸入向量，因為這個問題比較簡單，所以很多矩陣都退化成了1x1的標量。

該式計算出的結果，被稱為“先驗估計”，其右上角帶個減號，所謂先驗和減號，其物理意義就是，待會還要修正這個估計的值。

（2）寫出對預測模型的不確定度，也即狀態協方差矩陣P

上式中，F為狀態轉移矩陣，Pk-1為上一運算週期修正過的狀態協方差矩陣（若本次計算為首次計算，那麼Pk-1就是狀態協方差矩陣的初值），Q為狀態轉移協方差矩陣，我們對預測模型的不確定度進行了定量計算，顯然它由兩部分組成：①數學模型中

在那個英文的卡爾曼視訊中講到，對於狀態向量只含一個元素的系統，P矩陣其實就是“先驗估計”的方差；如果狀態向量含有多個元素，那麼P矩陣就是所有狀態變數預測誤差的協方差矩陣，這就是P矩陣的名字“狀態協方差矩陣”的來歷。顯然P矩陣代表了預測模型的不確定度。