五十道程式設計小題目 --- 28 八大排序演算法 java 00
【程式28】
題目:對10個數進行排序
1.程式分析:八大排序演算法
擴充套件:八大排序演算法
排序有內部排序和外部排序,內部排序是資料記錄在記憶體中進行排序,而外部排序是因排序的資料很大,一次不能容納全部的排序記錄,在排序過程中需要訪問外存。
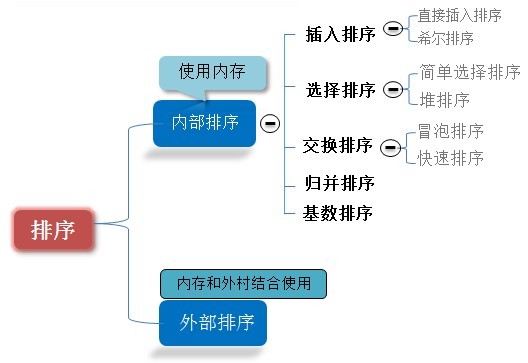
當n較大,則應採用時間複雜度為O(nlog2n)的排序方法:快速排序、堆排序或歸併排序序。
快速排序:是目前基於比較的內部排序中被認為是最好的方法,當待排序的關鍵字是隨機分佈時,快速排序的平均時間最短;
1.插入排序—直接插入排序(Straight Insertion Sort)
基本思想:
將一個記錄插入到已排序好的有序表中,從而得到一個新,記錄數增1的有序表。即:先將序列的第1個記錄看成是一個有序的子序列,然後從第2個記錄逐個進行插入,直至整個序列有序為止。
要點:設立哨兵,作為臨時儲存和判斷陣列邊界之用。
直接插入排序示例:
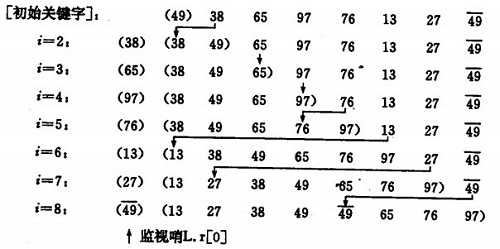
如果碰見一個和插入元素相等的,那麼插入元素把想插入的元素放在相等元素的後面。所以,相等元素的前後順序沒有改變,從原無序序列出去的順序就是排好序後的順序,所以插入排序是穩定的。
演算法的實現:
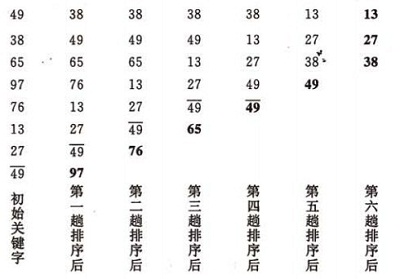
輸出結果:public class StraihtInertionSort { //快速排序演算法 public static int[] sort(int[] arr){ int n = arr.length; for(int i=0; i<n-1 ; i++){ if(arr[i] > arr[i+1]){ //交換 int tmp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = tmp; int index = i; //由於上面的交換,arr[i] < arr[i+1]的 , 所以index儲存的是即將要與前面所有數比較的索引即監視哨 int j=i-1; while( j>=0 && arr[j] > arr[index] ){ //交換 int tmp1 = arr[j]; arr[j] = arr[index]; arr[index] = tmp1; index = j; j--; } } } return arr; } //列印陣列 public static void print(int[] arr){ for(int i=0; i<arr.length ; i++){ System.out.print(arr[i] + " "); } System.out.println(); } public static void main(String[] args) { int[] arr = {49,38,65,97,76,13,27,49}; print(arr); print(sort(arr)); } }
49 38 65 97 76 13 27 49
13 27 38 49 49 65 76 97 效率:
時間複雜度:O(n^2).
2. 插入排序—希爾排序(Shell`s Sort)
希爾排序是1959 年由D.L.Shell 提出來的,相對直接排序有較大的改進。希爾排序又叫縮小增量排序
基本思想:
先將整個待排序的記錄序列分割成為若干子序列分別進行直接插入排序,待整個序列中的記錄“基本有序”時,再對全體記錄進行依次直接插入排序。
操作方法:
- 選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列個數k,對序列進行k 趟排序;
- 每趟排序,根據對應的增量ti,將待排序列分割成若干長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
希爾排序的示例:
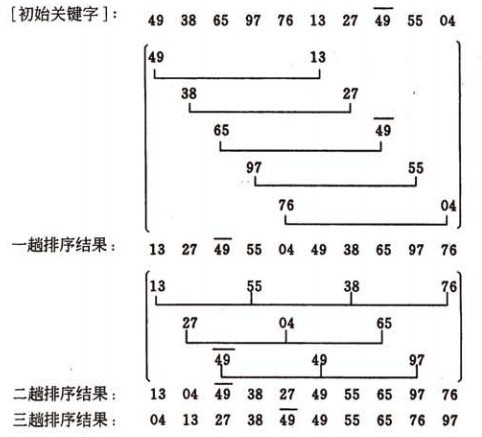
演算法實現:
我們簡單處理增量序列:增量序列d = {n/2 ,n/4, n/8 .....1} n為要排序數的個數
即:先將要排序的一組記錄按某個增量d(n/2,n為要排序數的個數)分成若干組子序列,每組中記錄的下標相差d.對每組中全部元素進行直接插入排序,然後再用一個較小的增量(d/2)對它進行分組,在每組中再進行直接插入排序。繼續不斷縮小增量直至為1,最後使用直接插入排序完成排序。
import java.util.Random;
public class ShellSort {
//希爾排序
public static int[] shellSort(int[] arr){
/*//確定增量序列
double n = arr.length;
int[] d = new int[(int)n]; //增量序列
for(int i=0; i<n; i++){
if(n > 0){
d[i] = (int) Math.ceil(n/2);
n = (int) Math.ceil(n/2);
if( n <= 3 ){
d[i+1] = 1;
break;
}
}
}
System.out.println("增量序列:");
print(d);*/
double n = arr.length; //n 定義為double很重要。如果是int ,這(int)Math.ceil(5/2)==2。如果是double,(int)Math.ceil(5/2)==3
for(int i=(int)Math.ceil(n/2) ; i>0 ; i=(int)Math.ceil(n/2) ){ //增量序列:
if( i==2 && n%2 != 0){ //如果是n=5時,下一個增量應該是3,在下一個增量應該是1,去除2,
n=i; //但是, 如果是n=4時,下一個增量應該是2, 此時增量為2 ,應該被保留
continue;
}
for(int j=0; j<n ;j++ ){ //趟數,趟數與增量相同
int k = j;
while(k+i<arr.length){ //分組,將arr 分組為相隔i的幾組,然後一個一個比較
if ( arr[k] > arr[k + i]) {
int tmp = arr[k];
arr[k] = arr[k + i];
arr[k + i] = tmp;
}
k = k+i;
}
}
n = i;
System.out.print("增量為" + i + "時,排序為 : ");
print(arr);
if(n==1){ // 因為double n=1,時 (int)Math.ceil(n/2)==1,如果不寫break,這裡會一直迴圈
break;
}
}
return arr;
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr2 = {49,38,65,97,76,13,27,49,55,04};
System.out.println("排序前 : ");
print(arr2);
System.out.println("排序後 : ");
print(shellSort(arr2));
//測試:
System.out.println();
System.out.println("任意陣列測試:");
Random r = new Random();
int[] testArr = new int[20];
for (int i = 0; i < 20; i++) {
testArr[i] = r.nextInt(100);
}
System.out.println("排序前 : ");
print(testArr);
System.out.println("排序後 : ");
print(shellSort(testArr));
}
}
輸出結果:
排序前 :
49 38 65 97 76 13 27 49 55 4
排序後 :
增量為5時,排序為 : 13 27 49 55 4 49 38 65 97 76
增量為3時,排序為 : 13 4 49 38 27 49 55 65 97 76
增量為1時,排序為 : 4 13 27 38 49 49 55 65 76 97
4 13 27 38 49 49 55 65 76 97
任意陣列測試:
排序前 :
38 57 9 30 49 27 45 83 88 76 14 53 16 58 77 21 20 40 55 94
排序後 :
增量為10時,排序為 : 14 53 9 30 49 21 20 40 55 76 38 57 16 58 77 27 45 83 88 94
增量為5時,排序為 : 14 20 9 30 49 21 45 16 55 76 27 53 40 58 77 38 57 83 88 94
增量為3時,排序為 : 14 20 9 30 16 21 40 27 53 38 49 55 45 57 77 76 58 83 88 94
增量為1時,排序為 : 14 9 16 20 21 27 30 38 40 49 45 53 55 57 58 76 77 83 88 94
14 9 16 20 21 27 30 38 40 49 45 53 55 57 58 76 77 83 88 94
希爾排序時效分析很難,關鍵碼的比較次數與記錄移動次數依賴於增量因子序列d的選取,特定情況下可以準確估算出關鍵碼的比較次數和記錄的移動次數。目前還沒有人給出選取最好的增量因子序列的方法。增量因子序列可以有各種取法,有取奇數的,也有取質數的,但需要注意:增量因子中除1 外沒有公因子,且最後一個增量因子必須為1。希爾排序方法是一個不穩定的排序方法。
3. 選擇排序—簡單選擇排序(Simple Selection Sort)
基本思想:
在要排序的一組數中,選出最小(或者最大)的一個數,用第1個位置的數與剩下的n-1個數進行比較,然後,用第2個位置的數與剩下的n-2個數進行比較,以此類推。
簡單選擇排序的示例:
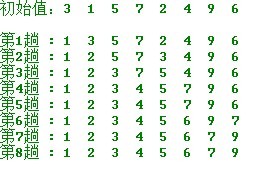
演算法實現:
import java.util.Random;
public class SimpleSelectionSort {
//簡單選擇排序
public static int[] ssSort(int[] arr){
for(int i=0; i<arr.length-1; i++){
for(int j=i+1; j<arr.length; j++){
if(arr[i] > arr[j]){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
}
return arr;
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
System.out.println("任意陣列測試:");
Random r = new Random();
int[] testArr = new int[20];
for (int i = 0; i < 20; i++) {
testArr[i] = r.nextInt(100);
}
System.out.println("排序前 : ");
print(testArr);
System.out.println("排序後 : ");
print(ssSort(testArr));
}
}
任意陣列測試:
排序前 :
27 21 8 56 28 19 40 72 80 84 85 31 99 25 11 62 8 67 60 94
排序後 :
8 8 11 19 21 25 27 28 31 40 56 60 62 67 72 80 84 85 94 99
4.選擇序—堆排序(Heap Sort)
堆排序是一種樹形選擇排序,是對直接選擇排序的有效改進。基本思想:
堆的定義如下:具有n個元素的序列(k1,k2,...,kn),當且僅當滿足
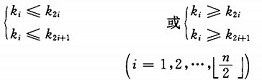
時稱之為堆。由堆的定義可以看出,堆頂元素(即第一個元素)必為最小項(小頂堆)。
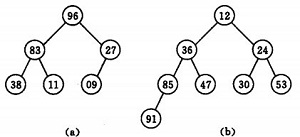
若以一維陣列儲存一個堆(Java陣列從0開始,i為0到n-1),則堆對應一棵完全二叉樹,且所有非葉結點的值均不大於(或不小於)其子女的值,根結點(堆頂元素)的值是最小(或最大)的。如:
(a)大頂堆序列:(96, 83,27,38,11,09)
(b) 小頂堆序列:(12,36,24,85,47,30,53,91)
1.堆
堆實際上是一棵完全二叉樹,其任何一非葉節點滿足性質:
Key[i] <= key[2i+1] && Key[i] <= key[2i+2]
或者
Key[i] >= Key[2i+1] && key >= key[2i+2]即任何一非葉節點的關鍵字不大於或者不小於其左右孩子節點的關鍵字。
堆分為大頂堆和小頂堆,
滿足 Key[i] >= Key[2i+1] && key >= key[2i+2] 稱為大頂堆,滿足 Key[i] <= key[2i+1] && Key[i] <= key[2i+2] 稱為小頂堆。由上述性質可知大頂堆的堆頂的關鍵字肯定是所有關鍵字中最大的,小頂堆的堆頂的關鍵字是所有關鍵字中最小的。
2.堆排序的思想
利用大頂堆(小頂堆)堆頂記錄的是最大關鍵字(最小關鍵字)這一特性,使得每次從無序中選擇最大記錄(最小記錄)變得簡單。
其基本思想為(大頂堆):
1)將初始待排序關鍵字序列(R1,R2....Rn)構建成大頂堆,此堆為初始的無序區;
2)將堆頂元素R[1]與最後一個元素R[n]交換,此時得到新的無序區(R1,R2,......Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n];
3)由於交換後新的堆頂R[1]可能違反堆的性質,因此需要對當前無序區(R1,R2,......Rn-1)調整為新堆,然後再次將R[1]與無序區最後一個元素交換,得到新的無序區(R1,R2....Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1,則整個排序過程完成。
操作過程如下:
1)初始化堆:將R[1..n]構造為堆;
2)將當前無序區的堆頂元素R[1]同該區間的最後一個記錄交換,然後將新的無序區調整為新的堆。
因此對於堆排序,最重要的兩個操作就是構造初始堆和調整堆,其實構造初始堆事實上也是調整堆的過程,只不過構造初始堆是對所有的非葉節點都進行調整。
下面舉例說明:
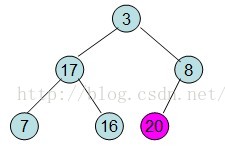
給定一個整形陣列a[]={16,7,3,20,17,8}(小頂堆),對其進行堆排序。
首先根據該陣列元素構建一個完全二叉樹,得到
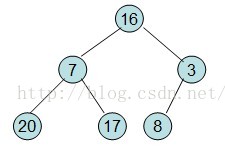
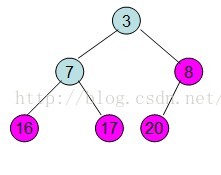
然後需要構造初始堆,則從最後一個非葉節點開始調整,調整過程如下:
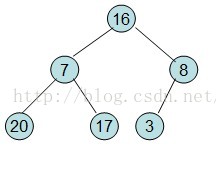
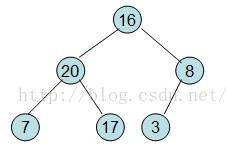
20和16交換後導致16不滿足堆的性質,因此需重新調整
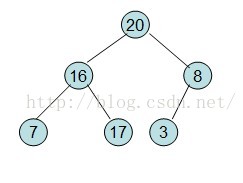
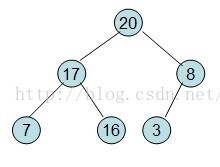
這樣就得到了初始堆。
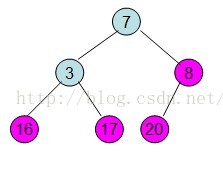
即每次調整都是從父節點、左孩子節點、右孩子節點三者中選擇最大者跟父節點進行交換(交換之後可能造成被交換的孩子節點不滿足堆的性質,因此每次交換之後要重新對被交換的孩子節點進行調整)。有了初始堆之後就可以進行排序了。
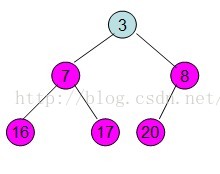
此時3位於堆頂不滿堆的性質,則需調整繼續調整
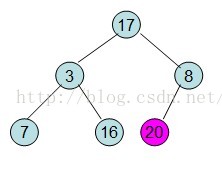
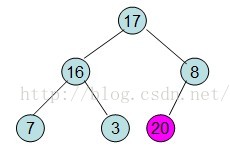
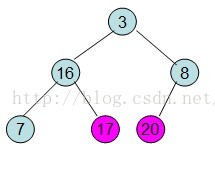
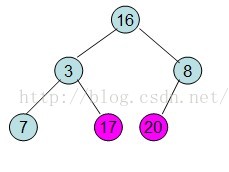
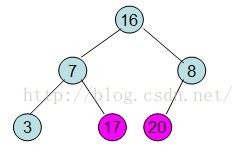
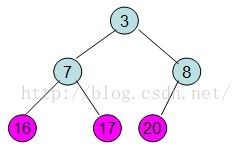
這樣整個區間便已經有序了。
從上述過程可知,堆排序其實也是一種選擇排序,是一種樹形選擇排序。只不過直接選擇排序中,為了從R[1...n]中選擇最大記錄,需比較n-1次,然後從R[1...n-2]中選擇最大記錄需比較n-2次。事實上這n-2次比較中有很多已經在前面的n-1次比較中已經做過,而樹形選擇排序恰好利用樹形的特點儲存了部分前面的比較結果,因此可以減少比較次數。對於n個關鍵字序列,最壞情況下每個節點需比較log2(n)次,因此其最壞情況下時間複雜度為nlogn。堆排序為不穩定排序,不適合記錄較少的排序。
import java.util.Random;
public class HeapSort {
public static int[] heapSort(int[] arr) {
System.out.println("----------------建堆----------------");
int lastIndex = 0;
for (int i = 0; i < arr.length; i++) {
lastIndex = arr.length - 1 - i;
createHeap(arr, lastIndex); // 建初始堆(大頂堆)
isHeap(arr, lastIndex);// 檢查堆還有沒有不滿足性質的
swap(arr, 0, arr.length - 1 - i); // 堆頂元素與葉子元素交換
System.out.println("堆頂與第"+(lastIndex+1)+"個數交換後 :");
print(arr);
System.out.println("----------------建堆----------------");
}
return arr;
}
//大頂堆
private static void createHeap(int[] arr, int lastIndex) {
int j = lastIndex;
int i = 0;
for (i = (lastIndex - 1) / 2; i >= 0; i--) {// 初始i等於lastIndex 的父節點
// 儲存當前正在判斷的節點
int k = i;
// 若當前節點的子節點存在
if ((2 * k) + 1 <= j) {
// biggerIndex總是記錄較大節點的值,先賦值為當前i節點的左子節點
int biggerIndex = 2 * k + 1;
if (biggerIndex < j) {//如果有右節點
// 若右子節點存在,則判斷左子節點與右子節點誰大,將大的放入biggerIndex
if (arr[biggerIndex] < arr[j]) {
biggerIndex++;
}
}
if (arr[k] < arr[biggerIndex]) {
// 若當前節點值比子節點最大值小,則交換2者得值,交換後將biggerIndex值賦值給k
swap(arr, k, biggerIndex);
j = (--k) * 2 + 2; //j 一直為k的右子節點
// k = biggerIndex;
}else{
j = (--k) * 2 + 2;//j 一直為k的右子節點
}
}
print(arr);
}
}
// 檢查堆是否都滿足大頂堆得性質
private static void isHeap(int[] arr, int lastIndex) {
int leftIndex = 0;
int rightIndex = 0;
int parent = 0;
for (int i = 0; i < (arr.length - 2) / 2; i++) {
leftIndex = 2 * i + 1;
rightIndex = 2 * i + 2;
parent = i;
if (arr[leftIndex] > arr[parent] || arr[rightIndex] > arr[parent]) {
createHeap(arr, lastIndex);
}
}
}
// 交換陣列元素
private static void swap(int[] arr, int i, int j) {
if (i == j) {
return;
}
arr[i] = arr[i] + arr[j];
arr[j] = arr[i] - arr[j];
arr[i] = arr[i] - arr[j];
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
System.out.println("任意陣列測試:");
Random r = new Random();
int[] testArr = new int[20];
for (int i = 0; i < 20; i++) {
testArr[i] = r.nextInt(100);
}
int a[] = { 16, 7, 3, 20, 17, 8 };
System.out.println("排序前 : ");
print(a);
System.out.println("排序 : ");
print(heapSort(a)); //得到小頂堆
/*
* System.out.println("排序前 : "); print(testArr);
*
* System.out.println("排序 : "); print(heapSort(testArr));
*/
}
}
</pre><pre>任意陣列測試:
排序前 :
16 7 3 20 17 8
排序 :
----------------建堆----------------
16 7 8 20 17 3
16 20 8 7 17 3
20 16 8 7 17 3
20 16 8 7 17 3
20 17 8 7 16 3
20 17 8 7 16 3
堆頂與第6個數交換後 :
3 17 8 7 16 20
----------------建堆----------------
3 17 8 7 16 20
17 3 8 7 16 20
17 16 8 7 3 20
17 16 8 7 3 20
堆頂與第5個數交換後 :
3 16 8 7 17 20
----------------建堆----------------
3 16 8 7 17 20
16 3 8 7 17 20
16 7 8 3 17 20
16 7 8 3 17 20
堆頂與第4個數交換後 :
3 7 8 16 17 20
----------------建堆----------------
8 7 3 16 17 20
8 7 3 16 17 20
堆頂與第3個數交換後 :
3 7 8 16 17 20
----------------建堆----------------
7 3 8 16 17 20
7 3 8 16 17 20
7 3 8 16 17 20
堆頂與第2個數交換後 :
3 7 8 16 17 20
----------------建堆----------------
3 7 8 16 17 20
3 7 8 16 17 20
3 7 8 16 17 20
堆頂與第1個數交換後 :
3 7 8 16 17 20
----------------建堆----------------
3 7 8 16 17 20
(本人寫的程式碼輸出結果意在看排列的過程,請去除重複後,再與下面結論進行比較驗證)
分析:
設樹深度為k,![]() 。從根到葉的篩選,元素比較次數至多2(k-1)次,交換記錄至多k
次。所以,在建好堆後,排序過程中的篩選次數不超過下式:
。從根到葉的篩選,元素比較次數至多2(k-1)次,交換記錄至多k
次。所以,在建好堆後,排序過程中的篩選次數不超過下式:
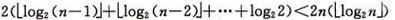
而建堆時的比較次數不超過4n 次,因此堆排序最壞情況下,時間複雜度也為:O(nlogn )。
5. 交換排序—氣泡排序(Bubble Sort)
基本思想:
在要排序的一組數中,對當前還未排好序的範圍內的全部數,自上而下對相鄰的兩個數依次進行比較和調整,讓較大的數往下沉,較小的往上冒。即:每當兩相鄰的數比較後發現它們的排序與排序要求相反時,就將它們互換。
氣泡排序的示例:
演算法的實現:
import java.util.Random;
public class BubbleSort {
public static void main(String[] args) {
int[] arr = new int[10];
Random r = new Random();
for(int i=0; i<10 ; i++){
arr[i] = r.nextInt(100);
}
for(int i=0; i<10 ; i++){
System.out.print(arr[i] + " ");
}
System.out.println();
int minIndex = 0;
for(int i=0; i< arr.length; i++){ //趟數
for(int j=0; j<arr.length-i-1; j++){//比較
if(arr[j] > arr[j+1]){
int tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
for(int i=0; i<10 ; i++){
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
輸出結果:
2 24 41 14 63 2 38 11 12 78
2 2 11 12 14 24 38 41 63 78 6. 交換排序—快速排序(Quick Sort)
快速排序和歸併排序都使用分治法來設計演算法,區別在於歸併排序把陣列分為兩個基本等長的子陣列,分別排好序之後還要進行歸併(Merge)操作,而快速排序拆分子陣列的時候顯得更有藝術,取一個基準元素,拆分之後基準元素左邊的元素都比基準元素小,右邊的元素都不小於基準元素,這樣只需要分別對兩個子陣列排序即可,不再像歸併排序一樣需要歸併操作。
基本思想:
1)選擇一個基準元素,通常選擇第一個元素或者最後一個元素,
2)通過一趟排序講待排序的記錄分割成獨立的兩部分,其中一部分記錄的元素值均比基準元素值小。另一部分記錄的 元素值比基準值大。
3)此時基準元素在其排好序後的正確位置
4)然後分別對這兩部分記錄用同樣的方法繼續進行排序,直到整個序列有序。
快速排序的示例:
(a)一趟排序的過程:

(b)排序的全過程

演算法的實現:
import java.util.Random;
public class QuickSort {
// 快速排序
private static void quickSort(int[] a) {
System.out.println("在陣列中從0到"+(a.length-1)+"基準元素索引:" + 0);
subQuickSort(a, 0, a.length-1);
}
private static void subQuickSort(int[] a,int start, int end) {
if(a == null || end-start<2){
return ;
}
int keyIndex = quickSortPortion(a, start, end);
System.out.println("在陣列中從"+start+"到"+end+"基準元素索引變換:" + keyIndex);
if(keyIndex == start){
subQuickSort(a, start+1, end);
}else if(keyIndex == end){
subQuickSort(a, start, end-1);
}else{
subQuickSort(a, start, keyIndex-1);
subQuickSort(a, keyIndex+1, end);
}
}
private static int quickSortPortion(int[] a, int start, int end) {
int minIndex = (end-start) / 2 + start; // minIndex定義為陣列的中間索引
int key = start; // 將陣列的第一個元素的索引定義為基準元素
int h = end;
System.out.println("快速排序------------>");
for (int i = start; i < end; i++) { // 比較 length-1次
if (key <= minIndex) { // 如果基準元素在前半部分
if (a[key] > a[h]) { // 元素值比基準元素值小
swap(a, key, h); // 交換位置
int tmp = h;
h = key + 1;
key = tmp;
} else {
h--;
}
} else { // 如果基準元素在後半部分
if (a[key] < a[h]) { // 元素值比基準元素值大
swap(a, key, h); // 交換位置
int tmp = key;
key = h;
h = tmp - 1;
} else {
h++;
}
}
print(a);
}
// print(a);
return key;
}
// 交換陣列元素
private static void swap(int[] arr, int i, int j) {
if (i == j) {
return;
}
arr[i] = arr[i] + arr[j];
arr[j] = arr[i] - arr[j];
arr[i] = arr[i] - arr[j];
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
System.out.println("排序前 : ");
print(a);
System.out.println("排序 : ");
quickSort(a);
print(a);
// System.out.println("任意陣列測試:");
// Random r = new Random();
// int[] testArr = new int[20];
// for (int i = 0; i < 20; i++) {
// testArr[i] = r.nextInt(100);
// }
//
// System.out.println("排序前 : ");
// print(testArr);
//
// System.out.println("排序後: ");
// print(quickSort(testArr));
}
}
輸出結果:
排序前 :
49 38 65 97 76 13 27 49
排序後 :
在陣列中從0到7基準元素索引:0
快速排序------------>
49 38 65 97 76 13 27 49
27 38 65 97 76 13 49 49
27 38 65 97 76 13 49 49
27 38 49 97 76 13 65 49
27 38 13 97 76 49 65 49
27 38 13 49 76 97 65 49
27 38 13 49 76 97 65 49
在陣列中從0到7基準元素索引變換:3
快速排序------------>
13 38 27 49 76 97 65 49
13 27 38 49 76 97 65 49
在陣列中從0到2基準元素索引變換:1
快速排序------------>
13 27 38 49 49 97 65 76
13 27 38 49 49 76 65 97
13 27 38 49 49 65 76 97
在陣列中從4到7基準元素索引變換:6
13 27 38 49 49 65 76 97
分析:
快速排序是一個不穩定的排序方法。
7. 歸併排序(Merge Sort)
基本思想:
歸併(Merge)排序法是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。
歸併排序示例:
合併方法:
設r[i…n]由兩個有序子表r[i…m]和r[m+1…n]組成,兩個子表長度分別為m+1-i 、n+1-m。
- j=m+1;k=i;i=i; //置兩個子表的起始下標及輔助陣列的起始下標
- 若i>m 或j>n,轉⑷ //其中一個子表已合併完,比較選取結束
- //選取r[i]和r[j]較小的存入輔助陣列rf
如果r[i]<r[j],rf[k]=r[i]; i++; k++; 轉⑵
否則,rf[k]=r[j]; j++; k++; 轉⑵ - //將尚未處理完的子表中元素存入rf
如果i<=m,將r[i…m]存入rf[k…n] //前一子表非空
如果j<=n , 將r[j…n] 存入rf[k…n] //後一子表非空 - 合併結束。
public class MergeSort2 {
private static void mergeSort(int[] a) {
double len = a.length;
int time = (int)len >> 1; //相當於len/2 ,即歸併的趟數
for(int i=0; i<time; i++){
int subLength = 1 << i; //相當於2的i次方 ,子序列的長度
int subNum = (int) Math.ceil(len/((subLength+1)*(i+1))); //子序列數
for(int j=0; j<subNum; j++){
int a1_start = (int) (j*2*subLength< len ? j*2*subLength : len-1); //即下一組歸併開始索引與上一組相差值
int a2_start = (int) (a1_start+subLength < len ? a1_start+subLength : len-1);
int a2_end = (int) ((a1_start+2*subLength-1) < len ? (a1_start+2*subLength-1): len-1); //防止最後一個越界
merge(a, a1_start, a2_start, a2_end);
}
System.out.println("-------------歸併排序後:-------------");
print(a);
System.out.println("************************************");
}
}
//歸併函式,傳入的引數分別為:原陣列,第一個字序列的開始索引,第二個字序列的開始索引,第二個字序列的結束索引
private static void merge(int[] a, int a1_start, int a2_start, int a2_end){
int len = a.length;
int[] rf = new int[a2_end-a1_start+1];
int i = a1_start, j = a2_start, k = 0;
while( i<a2_start && j <= a2_end){
if(a[i]<a[j]){
rf[k] = a[i];
i++;
k++;
}else{
rf[k] = a[j];
j++;
k++;
}
}
while(i<a2_start){
rf[k] = a[i];
k++;
i++;
}
while(j <= a2_end){
rf[k] = a[j];
k++;
j++;
}
//拷貝rf陣列,到原陣列 arraycopy(源陣列,源陣列開始索引,目標陣列,目標陣列開始索引,需要拷貝的長度);
System.arraycopy(rf,0,a,a1_start,rf.length);
print(a);
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int a[] = { 49, 38, 65, 97, 76, 13, 27};
System.out.println("排序前 : ");
print(a);
System.out.println("排序 : ");
mergeSort(a);
print(a);
}
}
排序前 :
49 38 65 97 76 13 27
排序 :
38 49 65 97 76 13 27
38 49 65 97 76 13 27
38 49 65 97 13 76 27
38 49 65 97 13 76 27
-------------歸併排序後:-------------
38 49 65 97 13 76 27
************************************
38 49 65 97 13 76 27
38 49 65 97 13 27 76
-------------歸併排序後:-------------
38 49 65 97 13 27 76
************************************
13 27 38 49 65 76 97
-------------歸併排序後:-------------
13 27 38 49 65 76 97
************************************
13 27 38 49 65 76 97
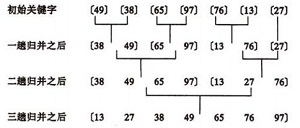
歸併的迭代演算法(方法二)
1 個元素的表總是有序的。所以對n 個元素的待排序列,每個元素可看成1 個有序子表。對子表兩兩合併生成n/2個子表,所得子表除最後一個子表長度可能為1 外,其餘子表長度均為2。再進行兩兩合併,直到生成n 個元素按關鍵碼有序的表。
public class MergeSort {
// private static long sum = 0;
/**
* <pre>
* 二路歸併
* 原理:將兩個有序表合併和一個有序表
* </pre>
*
* @param a
* @param s
* 第一個有序表的起始下標
* @param m
* 第二個有序表的起始下標
* @param t
* 第二個有序表的結束小標
*
*/
private static void merge(int[] a, int s, int m, int t) {
int[] tmp = new int[t - s + 1];
int i = s, j = m, k = 0;
while (i < m && j <= t) {
if (a[i] <= a[j]) {
tmp[k] = a[i];
k++;
i++;
} else {
tmp[k] = a[j];
j++;
k++;
}
}
while (i < m) {
tmp[k] = a[i];
i++;
k++;
}
while (j <= t) {
tmp[k] = a[j];
j++;
k++;
}
System.arraycopy(tmp, 0, a, s, tmp.length);
print(a);
}
/**
*
* @param a
* @param s
* @param len
* 每次歸併的有序集合的長度
*/
public static void mergeSort(int[] a, int s, int len) {
int size = a.length;
int mid = size / (len << 1); // size/(len*2)
int c = size & ((len << 1) - 1); // 判斷陣列長度奇偶數
// -------歸併到只剩一個有序集合的時候結束演算法-------//
if (mid == 0)
return;
// ------進行一趟歸併排序-------//
for (int i = 0; i < mid; ++i) {
s = i * 2 * len;
merge(a, s, s + len, (len << 1) + s - 1);
}
// -------將剩下的數和倒數一個有序集合歸併-------//
if (c != 0)
merge(a, size - c - 2 * len, size - c, size - 1);
// -------遞迴執行下一趟歸併排序------//
mergeSort(a, 0, 2 * len);
}
public static void main(String[] args) {
int[] a = new int[] {49, 38, 65, 97, 76, 13, 27 };
mergeSort(a, 0, 1);
for (int i = 0; i < a.length; ++i) {
System.out.print(a[i] + " ");
}
}
// 列印陣列
public static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
輸出結果:
38 49 65 97 76 13 27
38 49 65 97 76 13 27
38 49 65 97 13 76 27
38 49 65 97 13 27 76
38 49 65 97 13 27 76
13 27 38 49 65 76 97
13 27 38 49 65 76 97 8. 桶排序/基數排序(Radix Sort)
說基數排序之前,我們先說桶排序:
基本思想:是將陣列分到有限數量的桶子裡。每個桶子再個別排序(有可能再使用別的排序演算法或是以遞迴方式繼續使用桶排序進行排序)。桶排序是鴿巢排序的一種歸納結果。當要被排序的陣列內的數值是均勻分配的時候,桶排序使用線性時間(Θ(n))。但桶排序並不是 比較排序,他不受到 O(n log n) 下限的影響。
簡單來說,就是把資料分組,放在一個個的桶中,然後對每個桶裡面的在進行排序。
例如要對大小為[1..1000]範圍內的n個整數A[1..n]排序
首先,可以把桶設為大小為10的範圍,具體而言,設集合B[1]儲存[1..10]的整數,集合B[2]儲存 (10..20]的整數,……集合B[i]儲存( (i-1)*10, i*10]的整數,i = 1,2,..100。總共有 100個桶。
然後,對A[1..n]從頭到尾掃描一遍,把每個A[i]放入對應的桶B[j]中。 再對這100個桶中每個桶裡的數字排序,這時可用冒泡,選擇,乃至快排,一般來說任 何排序法都可以。
最後,依次輸出每個桶裡面的數字,且每個桶中的數字從小到大輸出,這 樣就得到所有數字排好序的一個序列了。
假設有n個數字,有m個桶,如果數字是平均分佈的,則每個桶裡面平均有n/m個數字。如果
對每個桶中的數字採用快速排序,那麼整個演算法的複雜度是
O(n + m * n/m*log(n/m)) = O(n + nlogn - nlogm)
從上式看出,當m接近n的時候,桶排序複雜度接近O(n)
當然,以上覆雜度的計算是基於輸入的n個數字是平均分佈這個假設的。這個假設是很強的 ,實際應用中效果並沒有這麼好。如果所有的數字都落在同一個桶中,那就退化成一般的排序了。
前面說的幾大排序演算法 ,大部分時間複雜度都是O(n2),也有部分排序演算法時間複雜度是O(nlogn)。而桶式排序卻能實現O(n)的時間複雜度。但桶排序的缺點是:
1)首先是空間複雜度比較高,需要的額外開銷大。排序有兩個陣列的空間開銷,一個存放待排序陣列,一個就是所謂的桶,比如待排序值是從0到m-1,那就需要m個桶,這個桶陣列就要至少m個空間。
2)其次待排序的元素都要在一定的範圍內等等。
桶式排序是一種分配排序。分配排序的特定是不需要進行關鍵碼的比較,但前提是要知道待排序列的一些具體情況。
分配排序的基本思想:說白了就是進行多次的桶式排序。
基數排序過程無須比較關鍵字,而是通過“分配”和“收集”過程來實現排序。它們的時間複雜度可達到線性階:O(n)。
例項:
撲克牌中52 張牌,可按花色和麵值分成兩個欄位,其大小關係為:
花色: 梅花< 方塊< 紅心< 黑心 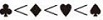
面值: 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A
若對撲克牌按花色、面值進行升序排序,得到如下序列: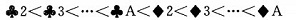
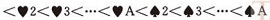
即兩張牌,若花色不同,不論面值怎樣,花色低的那張牌小於花色高的,只有在同花色情況下,大小關係才由面值的大小確定。這就是多關鍵碼排序。
為得到排序結果,我們討論兩種排序方法。
方法1:先對花色排序,將其分為4 個組,即梅花組、方塊組、紅心組、黑心組。再對每個組分別按面值進行排序,最後,將4 個組連線起來即可。
方法2:先按13 個面值給出13 個編號組(2 號,3 號,...,A 號),將牌按面值依次放入對應的編號組,分成13 堆。再按花色給出4 個編號組(梅花、方塊、紅心、黑心),將2號組中牌取出分別放入對應花色組,再將3 號組中牌取出分別放入對應花色組,……,這樣,4 個花色組中均按面值有序,然後,將4 個花色組依次連線起來即可。
設n 個元素的待排序列包含d 個關鍵碼{k1,k2,…,kd},則稱序列對關鍵碼{k1,k2,…,kd}有序是指:對於序列中任兩個記錄r[i]和r[j](1≤i≤j≤n)都滿足下列有序關係:
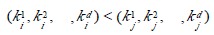
其中k1 稱為最主位關鍵碼,kd 稱為最次位關鍵碼 。
兩種多關鍵碼排序方法:
多關鍵碼排序按照從最主位關鍵碼到最次位關鍵碼或從最次位到