A. Opponents time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output

Arya has n opponents in the school. Each day he will fight with all opponents who are present this day. His opponents have some fighting plan that guarantees they will win, but implementing this plan requires presence of them all. That means if one day at least one of Arya's opponents is absent at the school, then Arya will beat all present opponents. Otherwise, if all opponents are present, then they will beat Arya.

For each opponent Arya knows his schedule — whether or not he is going to present on each particular day. Tell him the maximum number of consecutive days that he will beat all present opponents.

Note, that if some day there are no opponents present, Arya still considers he beats all the present opponents.

Input

The first line of the input contains two integers n and d (1 ≤ n, d ≤ 100) — the number of opponents and the number of days, respectively.

The i-th of the following d lines contains a string of length n consisting of characters '0' and '1'. The j-th character of this string is '0' if the j

-th opponent is going to be absent on the i-th day.

Output

Print the only integer — the maximum number of consecutive days that Arya will beat all present opponents.

Examples input

2 2
10
00

output

2

input

4 1
0100

output

1

input

4 5
1101
1111
0110
1011
1111

output

2

Note

In the first and the second samples, Arya will beat all present opponents each of the d days.

In the third sample, Arya will beat his opponents on days 1, 3 and 4 and his opponents will beat him on days 2 and 5. Thus, the maximum number of consecutive winning days is 2, which happens on days 3 and4.

題目大意：有d天，每天有n次挑戰，如果有一次挑戰中有結果0，就算今天勝利了，問最大連續勝利天數為多少。

思路：簡單模擬即可。

AC程式碼：

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
char a[105][105];
int main()
{
    int n,m;
    while(~scanf("%d%d",&m,&n))
    {
        for(int i=0;i<n;i++)
        {
            scanf("%s",a[i]);
        }
        int ans=0;
        int output=0;
        for(int i=0;i<n;i++)
        {
            int flag=1;
            for(int j=0;j<m;j++)
            {
                if(a[i][j]=='0')
                {
                    flag=0;
                    output++;
                    break;
                }
            }
            if(flag==0)
            {
                ans=max(ans,output);
            }
            else output=0;
        }
        printf("%d\n",ans);
    }
}

B. Lovely Palindromes time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output

Pari has a friend who loves palindrome numbers. A palindrome number is a number that reads the same forward or backward. For example 12321, 100001 and 1 are palindrome numbers, while 112 and 1021are not.

Pari is trying to love them too, but only very special and gifted people can understand the beauty behind palindrome numbers. Pari loves integers with even length (i.e. the numbers with even number of digits), so she tries to see a lot of big palindrome numbers with even length (like a 2-digit 11 or 6-digit 122221), so maybe she could see something in them.

Now Pari asks you to write a program that gets a huge integer n from the input and tells what is the n-th even-length positive palindrome number?

Input

The only line of the input contains a single integer n (1 ≤ n ≤ 10100 000).

Output

Print the n-th even-length palindrome number.

Examples input

1

output

11

input

10

output

1001

Note

The first 10 even-length palindrome numbers are 11, 22, 33, ... , 88, 99 and 1001.

題目大意：規定一個數是偶數長度的數，並且其是一個迴文數，問第n個這樣的數是多少。

思路：列舉找規律，發現第n個這樣的數就是其本身後邊加一個反著的本身，比如第10個數就是1001，第15個數就是1551.

Ac程式碼：

#include<stdio.h>
#include<string.h>
using namespace std;
char a[10000000];
int main()
{
    while(~scanf("%s",a))
    {
        printf("%s",a);
        int n=strlen(a);
        for(int i=n-1;i>=0;i--)
        {
            printf("%c",a[i]);
        }
        printf("\n");
    }
}

C. NP-Hard Problem time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

Recently, Pari and Arya did some research about NP-Hard problems and they found the minimum vertex cover problem very interesting.

Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edge uv there is at least one endpoint of it in this set, i.e. 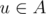 or  (or both).

Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.

They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A andB, such that both A and B are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).

Input

The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.

Each of the next m lines contains a pair of integers ui and vi (1  ≤  ui,  vi  ≤  n), denoting an undirected edge between ui and vi. It's guaranteed the graph won't contain any self-loops or multiple edges.

Output

If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).

If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integer k denoting the number of vertices in that vertex cover, and the second line contains k integers — the indices of vertices. Note that because of m ≥ 1, vertex cover cannot be empty.

Examples input

4 2
1 2
2 3

output

1
2 
2
1 3 

input

3 3
1 2
2 3
1 3

output

-1

Note

In the first sample, you can give the vertex number 2 to Arya and vertices numbered 1 and 3 to Pari and keep vertex number 4 for yourself (or give it someone, if you wish).

In the second sample, there is no way to satisfy both Pari and Arya.

題目大意：

給你n個點，m條邊，將其分成兩個集合，集合A是圖的一個點覆蓋，集合B也是圖的一個點覆蓋，要求集合A和集合B沒有交集，如果有這樣的兩個集合，在spj的情況下輸出合理解，如果沒有這樣的分配，輸出-1.

思路：

1、首先我們知道，如果圖是一個二分圖，那麼其必然有點覆蓋集，那麼點覆蓋集的補集，也一定是一個點覆蓋集。那麼問題就轉化到二分圖的判定上來。

2、二分圖的判定直接Bfs/Dfs，二分染色，如果遇到矛盾，輸出-1，如果沒遇到矛盾，那麼一直染色下去，注意這個圖是一個森林圖，所以我們要將所有點都進行染色分配集合。

AC程式碼：

#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
int color[100030];
vector<int >mp[100030];
int n,m;
int Bfs(int ss)
{
    color[ss]=1;
    queue<int >s;
    s.push(ss);
    while(!s.empty())
    {
        int u=s.front();
        s.pop();
        for(int i=0;i<mp[u].size();i++)
        {
            int v=mp[u][i];
            if(u==v)continue;
            if(color[v]==-1)
            {
                color[v]=3-color[u];
                s.push(v);
            }
            else
            {
                if(color[v]==color[u])return 0;
            }
        }
    }
    return 1;
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        memset(color,-1,sizeof(color));
        for(int i=1;i<=n;i++)mp[i].clear();
        for(int i=0;i<m;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            mp[x].push_back(y);
            mp[y].push_back(x);
        }
        int tt=1;
        for(int i=1;i<=n;i++)
        {
            if(color[i]==-1)
            {
                int ttt=Bfs(i);
                if(ttt==0)
                {
                    tt=0;break;
                }
            }
        }
        if(tt==0)
        {
            printf("-1\n");
        }
        else
        {
            int tot=0;
            for(int i=1;i<=n;i++)
            {
                if(color[i]==1)tot++;
            }
            printf("%d\n",tot);
            int f=0;
            for(int i=1;i<=n;i++)
            {
                if(color[i]==1)
                {
                    if(f==0)printf("%d",i),f=1;
                    else printf(" %d",i);
                }
            }
            printf("\n");
            tot=0;
            for(int i=1;i<=n;i++)
            {
                if(color[i]==2)tot++;
            }
            printf("%d\n",tot);
            f=0;
            for(int i=1;i<=n;i++)
            {
                if(color[i]==2)
                {
                    if(f==0)printf("%d",i),f=1;
                    else printf(" %d",i);
                }
            }
            printf("\n");
        }
    }
}