樸素貝葉斯的思想基礎是這樣的：對於給出的待分類項，求解在此項出現的條件下各個類別出現的概率，哪個最大，就認為此待分類項屬於哪個類別。通俗來說，就好比這麼個道理，你在街上看到一個黑人，我問你你猜這哥們哪裡來的，你十有八九猜非洲。為什麼呢？因為黑人中非洲人的比率最高，當然人家也可能是美洲人或亞洲人，但在沒有其它可用資訊下，我們會選擇條件概率最大的類別，這就是樸素貝葉斯的思想基礎。

      樸素貝葉斯分類的正式定義如下：

      1、設為一個待分類項，而每個a為x的一個特徵屬性。

      2、有類別集合。

      3、計算。

      4、如果，則。

      那麼現在的關鍵就是如何計算第3步中的各個條件概率。我們可以這麼做：

      1、找到一個已知分類的待分類項集合，這個集合叫做訓練樣本集。

      2、統計得到在各類別下各個特徵屬性的條件概率估計。即

           。

      3、如果各個特徵屬性是條件獨立的，則根據貝葉斯定理有如下推導：

      因為分母對於所有類別為常數，因為我們只要將分子最大化皆可。又因為各特徵屬性是條件獨立的，所以有：

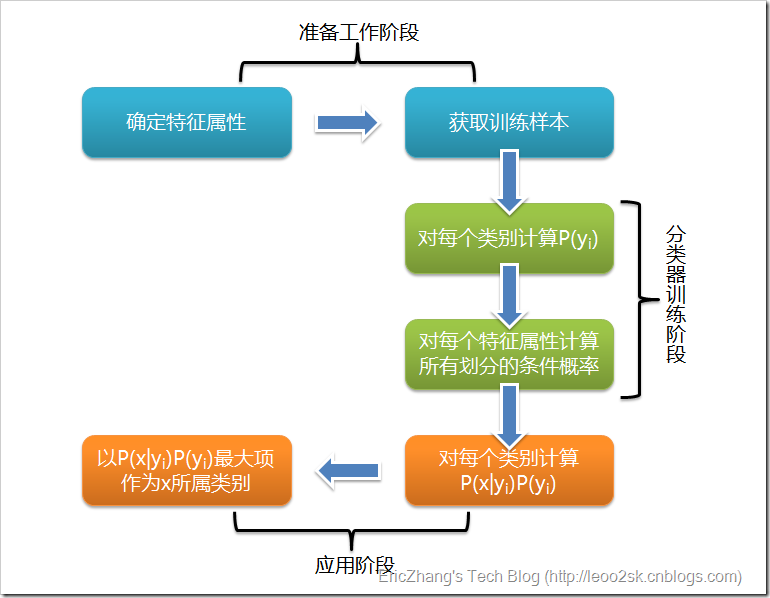
      根據上述分析，樸素貝葉斯分類的流程可以由下圖表示（暫時不考慮驗證）：

      可以看到，整個樸素貝葉斯分類分為三個階段：

      第一階段——準備工作階段，這個階段的任務是為樸素貝葉斯分類做必要的準備，主要工作是根據具體情況確定特徵屬性，並對每個特徵屬性進行適當劃分，然後由人工對一部分待分類項進行分類，形成訓練樣本集合。這一階段的輸入是所有待分類資料，輸出是特徵屬性和訓練樣本。這一階段是整個樸素貝葉斯分類中唯一需要人工完成的階段，其質量對整個過程將有重要影響，分類器的質量很大程度上由特徵屬性、特徵屬性劃分及訓練樣本質量決定。

      第二階段——分類器訓練階段，這個階段的任務就是生成分類器，主要工作是計算每個類別在訓練樣本中的出現頻率及每個特徵屬性劃分對每個類別的條件概率估計，並將結果記錄。其輸入是特徵屬性和訓練樣本，輸出是分類器。這一階段是機械性階段，根據前面討論的公式可以由程式自動計算完成。

      第三階段——應用階段。這個階段的任務是使用分類器對待分類項進行分類，其輸入是分類器和待分類項，輸出是待分類項與類別的對映關係。這一階段也是機械性階段，由程式完成。

1.4.2、估計類別下特徵屬性劃分的條件概率及Laplace校準

      由上文看出，計算各個劃分的條件概率P(a|y)是樸素貝葉斯分類的關鍵性步驟，當特徵屬性為離散值時，只要很方便的統計訓練樣本中各個劃分在每個類別中出現的頻率即可用來估計P(a|y)，下面重點討論特徵屬性是連續值的情況。

      當特徵屬性為連續值時，通常假定其值服從高斯分佈（也稱正態分佈）。即：

      而

      因此只要計算出訓練樣本中各個類別中此特徵項劃分的各均值和標準差，代入上述公式即可得到需要的估計值。均值與標準差的計算在此不再贅述。

      另一個需要討論的問題就是當P(a|y)=0怎麼辦，當某個類別下某個特徵項劃分沒有出現時，就是產生這種現象，這會令分類器質量大大降低。為了解決這個問題，我們引入Laplace校準，它的思想非常簡單，就是對沒類別下所有劃分的計數加1，這樣如果訓練樣本集數量充分大時，並不會對結果產生影響，並且解決了上述頻率為0的尷尬局面。

1.4.3、樸素貝葉斯分類例項：檢測SNS社群中不真實賬號

      下面討論一個使用樸素貝葉斯分類解決實際問題的例子，為了簡單起見，對例子中的資料做了適當的簡化。

      這個問題是這樣的，對於SNS社群來說，不真實賬號（使用虛假身份或使用者的小號）是一個普遍存在的問題，作為SNS社群的運營商，希望可以檢測出這些不真實賬號，從而在一些運營分析報告中避免這些賬號的干擾，亦可以加強對SNS社群的瞭解與監管。

      如果通過純人工檢測，需要耗費大量的人力，效率也十分低下，如能引入自動檢測機制，必將大大提升工作效率。這個問題說白了，就是要將社群中所有賬號在真實賬號和不真實賬號兩個類別上進行分類，下面我們一步一步實現這個過程。

      首先設C=0表示真實賬號，C=1表示不真實賬號。

1、確定特徵屬性及劃分

      這一步要找出可以幫助我們區分真實賬號與不真實賬號的特徵屬性，在實際應用中，特徵屬性的數量是很多的，劃分也會比較細緻，但這裡為了簡單起見，我們用少量的特徵屬性以及較粗的劃分，並對資料做了修改。

      我們選擇三個特徵屬性：a1：日誌數量/註冊天數，a2：好友數量/註冊天數，a3：是否使用真實頭像。在SNS社群中這三項都是可以直接從資料庫裡得到或計算出來的。

      下面給出劃分：a1：{a<=0.05, 0.05<a<0.2, a>=0.2}，a1：{a<=0.1, 0.1<a<0.8, a>=0.8}，a3：{a=0（不是）,a=1（是）}。

2、獲取訓練樣本

      這裡使用運維人員曾經人工檢測過的1萬個賬號作為訓練樣本。

3、計算訓練樣本中每個類別的頻率

      用訓練樣本中真實賬號和不真實賬號數量分別除以一萬，得到：

4、計算每個類別條件下各個特徵屬性劃分的頻率

5、使用分類器進行鑑別

      下面我們使用上面訓練得到的分類器鑑別一個賬號，這個賬號使用非真實頭像，日誌數量與註冊天數的比率為0.1，好友數與註冊天數的比率為0.2。

      可以看到，雖然這個使用者沒有使用真實頭像，但是通過分類器的鑑別，更傾向於將此賬號歸入真實賬號類別。這個例子也展示了當特徵屬性充分多時，樸素貝葉斯分類對個別屬性的抗干擾性。

1.5、分類器的評價

      雖然後續還會提到其它分類演算法，不過這裡我想先提一下如何評價分類器的質量。

      首先要定義，分類器的正確率指分類器正確分類的專案佔所有被分類專案的比率。

      通常使用迴歸測試來評估分類器的準確率，最簡單的方法是用構造完成的分類器對訓練資料進行分類，然後根據結果給出正確率評估。但這不是一個好方法，因為使用訓練資料作為檢測資料有可能因為過分擬合而導致結果過於樂觀，所以一種更好的方法是在構造初期將訓練資料一分為二，用一部分構造分類器，然後用另一部分檢測分類器的準確率。

貝葉斯網路

2.1、摘要

      在上一篇文章中我們討論了樸素貝葉斯分類。樸素貝葉斯分類有一個限制條件，就是特徵屬性必須有條件獨立或基本獨立（實際上在現實應用中幾乎不可能做到完全獨立）。當這個條件成立時，樸素貝葉斯分類法的準確率是最高的，但不幸的是，現實中各個特徵屬性間往往並不條件獨立，而是具有較強的相關性，這樣就限制了樸素貝葉斯分類的能力。這一篇文章中，我們接著上一篇文章的例子，討論貝葉斯分類中更高階、應用範圍更廣的一種演算法——貝葉斯網路（又稱貝葉斯信念網路或信念網路）。

2.2、重新考慮上一篇的例子

      上一篇文章我們使用樸素貝葉斯分類實現了SNS社群中不真實賬號的檢測。在那個解決方案中，我做了如下假設：

      i、真實賬號比非真實賬號平均具有更大的日誌密度、各大的好友密度以及更多的使用真實頭像。

      ii、日誌密度、好友密度和是否使用真實頭像在賬號真實性給定的條件下是獨立的。

      但是，上述第二條假設很可能並不成立。一般來說，好友密度除了與賬號是否真實有關，還與是否有真實頭像有關，因為真實的頭像會吸引更多人加其為好友。因此，我們為了獲取更準確的分類，可以將假設修改如下：

      i、真實賬號比非真實賬號平均具有更大的日誌密度、各大的好友密度以及更多的使用真實頭像。

      ii、日誌密度與好友密度、日誌密度與是否使用真實頭像在賬號真實性給定的條件下是獨立的。

      iii、使用真實頭像的使用者比使用非真實頭像的使用者平均有更大的好友密度。

      上述假設更接近實際情況，但問題隨之也來了，由於特徵屬性間存在依賴關係，使得樸素貝葉斯分類不適用了。既然這樣，我去尋找另外的解決方案。

      下圖表示特徵屬性之間的關聯：

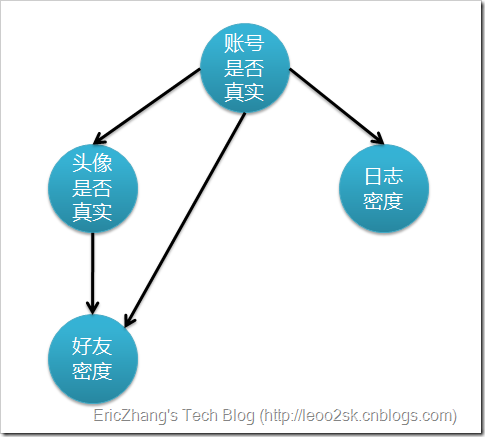
      上圖是一個有向無環圖，其中每個節點代表一個隨機變數，而弧則表示兩個隨機變數之間的聯絡，表示指向結點影響被指向結點。不過僅有這個圖的話，只能定性給出隨機變數間的關係，如果要定量，還需要一些資料，這些資料就是每個節點對其直接前驅節點的條件概率，而沒有前驅節點的節點則使用先驗概率表示。

      例如，通過對訓練資料集的統計，得到下表（R表示賬號真實性，H表示頭像真實性）：

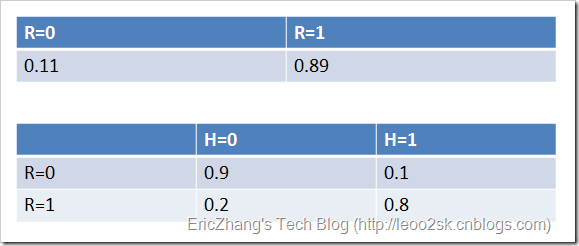
      縱向表頭表示條件變數，橫向表頭表示隨機變數。上表為真實賬號和非真實賬號的概率，而下表為頭像真實性對於賬號真實性的概率。這兩張表分別為“賬號是否真實”和“頭像是否真實”的條件概率表。有了這些資料，不但能順向推斷，還能通過貝葉斯定理進行逆向推斷。例如，現隨機抽取一個賬戶，已知其頭像為假，求其賬號也為假的概率：

      也就是說，在僅知道頭像為假的情況下，有大約35.7%的概率此賬戶也為假。如果覺得閱讀上述推導有困難，請複習概率論中的條件概率、貝葉斯定理及全概率公式。如果給出所有節點的條件概率表，則可以在觀察值不完備的情況下對任意隨機變數進行統計推斷。上述方法就是使用了貝葉斯網路。

2.3、貝葉斯網路的定義及性質

      有了上述鋪墊，我們就可以正式定義貝葉斯網路了。

      一個貝葉斯網路定義包括一個有向無環圖（DAG）和一個條件概率表集合。DAG中每一個節點表示一個隨機變數，可以是可直接觀測變數或隱藏變數，而有向邊表示隨機變數間的條件依賴；條件概率表中的每一個元素對應DAG中唯一的節點，儲存此節點對於其所有直接前驅節點的聯合條件概率。

      貝葉斯網路有一條極為重要的性質，就是我們斷言每一個節點在其直接前驅節點的值制定後，這個節點條件獨立於其所有非直接前驅前輩節點。

      這個性質很類似Markov過程。其實，貝葉斯網路可以看做是Markov鏈的非線性擴充套件。這條特性的重要意義在於明確了貝葉斯網路可以方便計算聯合概率分佈。一般情況先，多變數非獨立聯合條件概率分佈有如下求取公式：

      而在貝葉斯網路中，由於存在前述性質，任意隨機變數組合的聯合條件概率分佈被化簡成

      其中Parents表示xi的直接前驅節點的聯合，概率值可以從相應條件概率表中查到。

      貝葉斯網路比樸素貝葉斯更復雜，而想構造和訓練出一個好的貝葉斯網路更是異常艱難。但是貝葉斯網路是模擬人的認知思維推理模式，用一組條件概率函式以及有向無環圖對不確定性的因果推理關係建模，因此其具有更高的實用價值。

2.4、貝葉斯網路的構造及學習

      構造與訓練貝葉斯網路分為以下兩步：

      1、確定隨機變數間的拓撲關係，形成DAG。這一步通常需要領域專家完成，而想要建立一個好的拓撲結構，通常需要不斷迭代和改進才可以。

      2、訓練貝葉斯網路。這一步也就是要完成條件概率表的構造，如果每個隨機變數的值都是可以直接觀察的，像我們上面的例子，那麼這一步的訓練是直觀的，方法類似於樸素貝葉斯分類。但是通常貝葉斯網路的中存在隱藏變數節點，那麼訓練方法就是比較複雜，例如使用梯度下降法。由於這些內容過於晦澀以及牽扯到較深入的數學知識，在此不再贅述，有興趣的朋友可以查閱相關文獻。

2.5、貝葉斯網路的應用及示例

      貝葉斯網路作為一種不確定性的因果推理模型，其應用範圍非常廣，在醫療診斷、資訊檢索、電子技術與工業工程等諸多方面發揮重要作用，而與其相關的一些問題也是近來的熱點研究課題。例如，Google就在諸多服務中使用了貝葉斯網路。

      就使用方法來說，貝葉斯網路主要用於概率推理及決策，具體來說，就是在資訊不完備的情況下通過可以觀察隨機變數推斷不可觀察的隨機變數，並且不可觀察隨機變數可以多於以一個，一般初期將不可觀察變數置為隨機值，然後進行概率推理。下面舉一個例子。

      還是SNS社群中不真實賬號檢測的例子，我們的模型中存在四個隨機變數：賬號真實性R，頭像真實性H，日誌密度L，好友密度F。其中H，L，F是可以觀察到的值，而我們最關係的R是無法直接觀察的。這個問題就劃歸為通過H，L，F的觀察值對R進行概率推理。推理過程可以如下表示：

      1、使用觀察值例項化H,L和F，把隨機值賦給R。

      2、計算。其中相應概率值可以查條件概率表。

      由於上述例子只有一個未知隨機變數，所以不用迭代。更一般得，使用貝葉斯網路進行推理的步驟可如下描述：

      1、對所有可觀察隨機變數節點用觀察值例項化；對不可觀察節點例項化為隨機值。

      2、對DAG進行遍歷，對每一個不可觀察節點y，計算，其中wi表示除y以外的其它所有節點，a為正規化因子，sj表示y的第j個子節點。

      3、使用第三步計算出的各個y作為未知節點的新值進行例項化，重複第二步，直到結果充分收斂。

      4、將收斂結果作為推斷值。