2. 程式人生 > >演算法_6：分治策略

演算法_6：分治策略

阿新 • • 發佈：2019-02-11
  • 分解，解決，合併
  • 遞迴式的求解演算法：帶入，遞迴樹，主方法

最大子陣列問題

  • 最大子陣列的三種情況：A[low….mid]; A[mid+1……high]和跨域中點

FIND-MAX-CROSSING-SUBARRAY（A，low, mid, high）

返回：下標元組跨越中點的最大陣列的邊界，並返回最大陣列的中值和

FIND-MAX-CROSSING-SUBARRAY（A，low, mid, high）

1. left-sum=-無窮
2. sum=0
3. for i=mid down to low
4.      sum=sum+A[i]
5.      if
 
 sum >left-sum
6.         left-sum=sum
7.         max-left=i
8. right-low=-無窮
9. sum=0
10. for j=mid+1 to high
11.     sum=sum=A[j]
12.     if sum>right-sum
13.        right-sum=sum
14.        max-right=j
15.  return (max-left,max-right,left-sum+right-sum)
  • 演算法分析: O(n)
    A[low…high] 包含 n個元素

FIND-MAX-SUBARRAY演算法

//FIND-MAX-SUBARRAY(A,low,high)
1. if high==low
2.   return(low,high,A[low])
3. else mid= 下取整[(low+high)/2]
4.   (left-low,left-high,left-sum)=FIND-MAX-SUMARRAY(A,low,mid)
5.   (right-low,right-high,right-sum)=FIND-MAX-SUMARRAY(A,mid+1,high)
6.   (cross-low,cross-high,cross-sum)=FIND-MAX-CROSSING-SUMARRAY(A,low,mid
 
,high)
7. if left-sum>=right-sum and left-sm >=cross-sum
8.    return (left-low,left-high,left-sum)
9. else right-sum>=left-sum and right-sum>=cross-sum
10.   return (right-low,right-high,right-sum)
11. else return(corss-low,cross-high,cross-sum)

演算法分析

T(n){O(1).........若n=12T(n/2)+O(n)......其他
  • 複雜度：T(n)=O(nlng)

strassen演算法的矩陣乘法

暴力

  • 矩陣乘法, 計算n2個數
    Cij=∑nk=1aik∗bkj
//矩陣乘法
1. n=A.rows
2. let C be a new n*n matrix
3. for i=1 to n
4.   for j=1 to n
5.       c_ij=0
6.       for k=1 to n
7.           c_ij=c_ij+a_ik*b_kj
8. return C
  • 複雜度： O(n3)

簡單分治

[C11C21C12C22]=[A11A21A12A22]∗[B11B21B12B22] 
//直接遞迴
S-M-N-R(A,B)
1. n=A.rows
2. let C be n*n matrix
3. if n==1
4.    c_11=a_11*b_11
5. else partition A,B,C as 上式
6.    C_11=S-M-N-R(A_11,B_11)+S-M-N-R(A_12,B_21)
7. ......
8. return C
  • 複雜度
    1. n==1……….T(1)=O(1)
    2. n>1…………..遞迴
      T（n）=8T(n/2)+O(n^2)……….T(n)=O(n^3)

strassen

  1. n==1……….T(1)=O(1)

    1. n>1…………..遞迴
      T（n）=7T(n/2)+O(n^2)……….T(n)=O(n^3)

      • 複雜度減少到：O(nlg7)

代入法求解遞迴式

  1. 猜測解得形式
  2. 歸納法求解常數，證明正確性

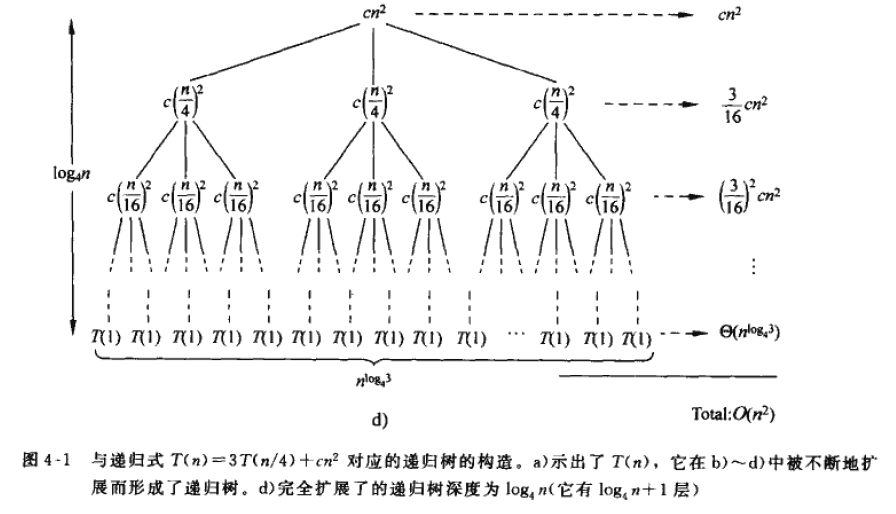
遞迴樹法

T(n)=3T(⌊n/4⌋)+cn2

  • 計算遞迴樹的高度
    n/4i=1..........i=log4n.........遞歸樹有log4n層

  • 每層代價，每層的結點數是上一層的3倍
    i 結點的結點數是3i

  • 每層的子問題規模是上一層的1/4

  • 第i層的代價nlog43個T（1）

這裡寫圖片描述

  • 整棵樹的 代價
    T(n)=cn2+316cn2+(316)cn2+......+(316log4(n−1))cn2+O(nlog43)
    <O(n2)

主方法

  • 遞迴式T(n)=aT(a/b)+f(n)
    1. 若對某個常數 ϵ >0 有 f(n)=O(nlogb(a

      相關推薦

      演算法_6：分治策略

      分解，解決，合併 遞迴式的求解演算法：帶入，遞迴樹，主方法 最大子陣列問題 最大子陣列的三種情況：A[low….mid]; A[mid+1……high]和跨域中點 FIND-M

      【C++實現】五大常用演算法之一：分治演算法（例項：漢諾塔）

      求解思想：大而化小 1、問題拆分成子問題 2、對子問題求解 在漢諾塔遊戲中，有三個分別命名為A、B、C得塔座，幾個大小各不相同，從小到大一次編號得圓盤，每個原盤中間有一個小孔。最初，所有得圓盤都在A塔座上，其中最大得圓盤在最下面，然後是第二大，以此類推. 先上程式

      五大常用演算法之一：分治演算法（轉）

      分治演算法 一、基本概念    在電腦科學中，分治法是一種很重要的演算法。字面上的解釋是“分而治之”，就是把一個複雜的問題分成兩個或更多的相同或相似的子問題，再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解，原問題的解即子問題的解的合併。這個技巧是很多高效演算法的基礎，如排序演算法(快速排序，

      五大常用演算法之一：分治演算法(轉載)

      轉載自：http://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741370.html 一、基本概念    在電腦科學中，分治法是一種很重要的演算法。字面上的解釋是“分而治之”，就是把一個複雜的問題分成兩個或更多的相

      演算法設計與分析筆記之(2)：遞迴與分治策略

      宣告 1）本文僅供學術交流，非商用。具體引用的資料請看參考文獻。如果某部分不小心侵犯了大家的利益，請聯絡博主刪除。 2）本人才疏學淺，整理總結的時候難免出錯，還望各位前輩不吝指正，謝謝。 聯

      演算法分析——分治策略

      1 分治策略概念 分治法是講一個複雜的問題分成兩個或者更多的相同或者相似的問題，這些子問題相互獨立或者形式相同，再把子問題分解成更小的子問題，一直這樣迴圈下去，直到最後子問題可以簡單的直接求解，原問題的解即子問題解得合併。 例1.1 給定一個順序表，編寫一個求出其最大值

      計算機演算法設計與分析之遞迴與分治策略——二分搜尋技術

      遞迴與分治策略 二分搜尋技術 　　我們所熟知的二分搜尋演算法是運用分治策略的典型例子，針對這個演算法，先給出一個簡單的案例。 　　目的：給定已排好序的n個元素a[0:n-1]，現要在這n個元素中找出一特定的元素x。 　　我們首先想到的最簡單的是用順序搜尋方法，逐個比較a[0:n-1]中元素，直至找出元

      影象演算法中的設計模式（一）：使用策略模式設計演算法

      設計模式（Design pattern）是一套被反覆使用、多數人知曉的、經過分類編目的、程式碼設計經驗的總結。總體來說，一個設計模式就是一個可重用的、讓程式碼更容易被他人理解的、可靠性的解決方案。 策略設計模式的目的就是把演算法封裝進類。封裝後，演算法之間互相

      演算法分析與設計實驗 分治策略 兩路合併排序和快速排序

      實驗目的理解分治法的演算法思想，閱讀實現書上已有的部分程式程式碼並完善程式， 加深對分治法 的演算法原理及實現過程的理解。實驗內容用分治法實現一組無序序列的兩路合併排序和快速排序。要求清楚合併排序及快速排序 的基本原理， 程式設計實現分別用這兩種方法將輸入的一組無序序列排序

      整數劃分演算法實現 分治策略

      將正整數n表示成一系列正整數之和。 正整數n的這種表示成為正整數n的劃分。 正整數n的不同的劃分個數成為正整數n的劃分數。 int q(int n,int m){ if((n<1)||(m&

      常用演算法：分治演算法、動態規劃演算法、貪心演算法、回溯法、分支限界法

      1、概念     回溯演算法實際上一個類似列舉的搜尋嘗試過程，主要是在搜尋嘗試過程中尋找問題的解，當發現已不滿足求解條件時，就“回溯”返回，嘗試別的路徑。    回溯法是一種選優搜尋法，按選優條件向前搜尋，以達到目標。但當探索到某一步時，發現原先選擇並不優或達不到目標，就退回一步重新選擇，這種走不通就退回再

      萬惡的期末考試---演算法複習---遞迴與分治策略（二分搜尋與大數乘法與矩陣對角線相加，strassen矩陣乘法，棋盤覆蓋）

      已經考過三科了，還有三科，明天下午就要考演算法了，心慌慌，抓緊寫個部落格做演算法複習，靜靜心 呃呃呃  說好的只是複習下，自己拓展到了天外 ，第二章還沒結束....程式碼如下 大數乘法過程如下： 二分搜尋與大數乘法與矩陣對角線相加 package chap2_dgfz

      演算法設計與分析之遞迴與分治策略

       分治法：     將一個難以直接解決的大問題，分割成一些規模較小的相同問題，以便各個擊破，分而治之。 (1)可行性：如果原問題可分割成k個子問題(1<k<=n),且這些子問題都可解，並可利用這些子問題的解求出原問題的解，那麼分治法就是可行的。 (2)分治法與

      演算法分析與設計----分治策略

      一、分治策略的基本思想 1.將原始問題劃分或者歸結為規模較小的子問題 2.遞迴或迭代的求解每個子問題 3.將子問題的解綜合得到原問題的解 注意： 1.子問題與原始問題性質完全一樣 2.子問題之間可彼此獨立求解 3.遞迴停止時，子問題足夠小可直接求解 二、應用 （一

      遞迴、分治策略、動態規劃以及貪心演算法之間的關係

      引言 最近集中研究計算智慧，其中涉及到遞迴和動態規劃，動態規劃實現中又用到了遞迴，忽然發現這兩個概念的差別分得不太清楚。索性把遞迴、分治策略、動態規劃、貪婪選擇之間的聯絡與區別都一併搞清楚吧。 1、分治策略（Divide and Conquer）

      演算法之分治策略與應用

      歸併排序中我們利用了分治策略，在分治策略中，我們遞迴求解一個問題，在每層遞迴中應用如下三個步驟： 分解：將問題劃分為一些子問題，子問題的形式與原問題一樣，只是規模更小。 解決：遞迴的求解出子問題。如

      南郵演算法分析與設計實驗1 分治策略

      分治策略 實驗目的： 理解分治法的演算法思想，閱讀實現書上已有的部分程式程式碼並完善程式，加深對分治法的演算法原理及實現過程的理解。 實驗內容： 用分治法實現一組無序序列的兩路合併排序和快速排序。要求清楚合併排序及快速排序的基本原理，程式設計實現分別用這兩種方法將輸入的

      Java語言描述：遞迴與分治策略之合併排序與快速排序

      合併排序： package DivideAndConquer; public class MergeSort { //一定要多傳入一個多餘的temp陣列用於存放排序的中間結果 public static<AnyType extends Comparable&l

      演算法中分治策略實現快速排序

      快速排序演算法是基於分治策略的一個排序演算法，其基本思想是，對於輸入的子陣列，按以下三個步驟求解： 1 分解：選擇一個基準元素，將整個陣列分為大於基準元素，等於基準元素，小於基準元素的三組。基準元素在

      演算法分析-最大連續子陣列（分治策略）

      大家好，我是三十三，第一次寫部落格，有什麼考慮不周的，請廣大同學多多指正。作為一個計算機專業毛都不會的即將畢業狗，說實話，心裡一點有一絲絲慌慌的。在即將畢業之際，自己還是想囤點貨給自己貼貼金，有啥錯誤還望指出。一、 實驗目的及任務分治法求解最大子陣列問題二、 實驗環境c++或