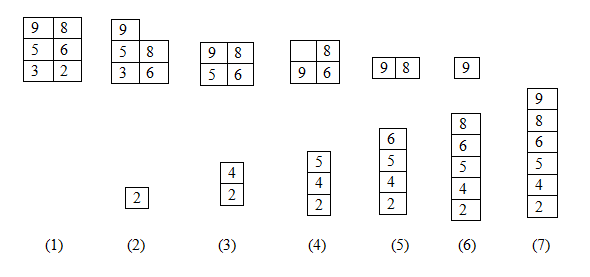
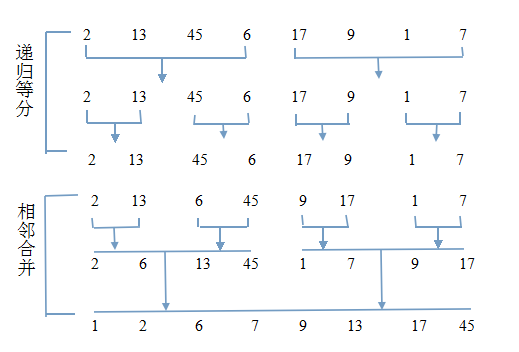
歸併排序:二路歸併
歸併排序(Merge Sort)是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個有序的子序列,再把有序的子序列合併為整體有序序列。
歸併排序的具體做法:
- 把原序列不斷地遞歸等分,直至每等份只有一個元素,此時每等份都是有序的。
- 相鄰等份合並,不斷合併,直至合併完全。
二路歸併
歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法(Divide
and Conquer)的一個非常典型的應用。歸併排序最常用的是二路歸併,即把兩個小的有序的序列和併成一個大的有序序列:合二為一。
一個二路歸併的流程圖是這樣的:
多路歸併無非是多個有序的小序列合併成一個大的有序序列,道理和二路歸併一樣。
先來看下如何把兩個有序的序列合併成一個大的有序序列,程式碼如下:
/* *把有序序列a和b,合併成c *該演算法成立前提: a和b已經有序 */ void merge(int a[], int na, int b[], int nb, int c[]) { if(a && b && c && na >0 && nb >0) { int i,j,k; i = j = k = 0; //不斷地比較a和b的頭部元素,較小的存入c while(i < na && j < nb) { if(a[i] <= b[j]) // <= 保持演算法的穩定性 c[k++] = a[i++]; else c[k++] = b[j++]; /*另一種更有效的做法是這樣的 while(i < na && a[i] <= b[j]) c[k++] = a[i++]; while(j < nb && b[j] < a[i]) c[k++] = b[j++]; */ } //把a或b中剩餘的元素直接存入c /* 也可以這樣: * memcpy(c+k, a+i, (na-i)sizeof(int)); * 下同 */ while(i < na) c[k++] = a[i++]; while(j < nb) c[k++] = b[j++]; } }
可以看出,二路歸併的時間複雜度是O(n),n是原序列的資料規模。以上程式碼是歸併排序的基礎,弄懂了它,就很好寫歸併排序了,看下歸併排序的流程圖:
可以看出,上半部分不斷地遞迴深入:不斷地均分原序列,直到每一部分只含有一個元素。下半部分,開始遞迴返回,通過反覆呼叫二路歸併演算法,把相鄰的有序子序列合併成一個規模更大的序列。
理解了這些,相信就很容易寫出歸併排序的程式碼了:
//把[first, mid]和[mid+1, last]範圍內的資料合併 void mergeArray(int a[], int b[], int first, int mid, int last) { int i, j, k; i = first, j = mid + 1, k = 0; while (i <= mid && j <= last) { while(i <= mid && a[i] <= a[j]) b[k++] = a[i++]; while(j <= last && a[j] < a[i]) b[k++] = a[j++]; } /* 也可以這樣: * memcpy(b+k, a+i, (mid-i+1)sizeof(int)); * 下同 */ while (i <= mid) b[k++] = a[i++]; while (j <= last) b[k++] = a[j++]; //[first,last]範圍內的資料已有序,則寫回原陣列 for (i = 0; i < k; i++) a[first + i] = b[i]; } void mergesort(int a[], int b[], int first, int last) { if (first < last) { int mid = first + ((last - first) >> 1); mergesort(a, b, first, mid); mergesort(a, b, mid + 1, last); mergeArray(a, b, first, mid, last); } } void MergeSort(int a[], int n) { if (a && n > 1) { int *b = new int[n]; //構建輔助陣列 mergesort(a, b, 0, n - 1); delete[]b; } }
在排序過程中,我們使用了一個相同大小的臨時輔助陣列。
演算法分析:
1.演算法的複雜度
對陣列長度為n的序列進行歸併排序,則大約要進行logn次歸併,每一次合併都是線性時間O(n)。故粗略的計算出歸併排序的時間複雜度是O(nlogn)(最好、最差都是這樣)。空間複雜度是O(n)。詳細的時間複雜度分析是這樣的:
對長度為n的序列歸併排序,需要遞迴的對長度為n/2的子序列進行歸併排序,最後把兩段子序列二路歸併。遞推關係是這樣的:T(n)=2T(n/2)+O(n),顯然T(1)=O(1),解得T(n)=o(nlogn)。
2.穩定性
歸併排序是穩定的,並且是時間複雜度為o(nlogn)的幾種排序(快速排序、堆排序)中唯一穩定的排序演算法。
3.儲存結構
順序儲存和鏈式儲存都行。
另外,歸併排序多用於外排序中。
若是有所幫助,頂一個哦!
所有內容的目錄