為什麼每次看到這種題的超簡短解題程式碼都會有一種“哇！”的感覺

題意

小Q非常富有，擁有非常多的硬幣，小Q的擁有的硬幣是有規律的，對於所有的非負整數K，小Q恰好各有兩個數值為2^k的硬幣，所以小Q擁有的硬幣是1，1，2，2，4，4，8，8……，小Q賣東西需要支付n元錢，請問小Q想知道有多少種組合方案。（如果兩種方案某個面值的硬幣選取的個數不一樣就考慮為不一樣的方案）

輸入

輸入：一個n (1<=n<=10^18),代表要付的錢
6

輸出

輸出：表示小Q可以拼湊的方案數目
3

思路

　　除了暴力法，毫無思路，真的不會，大家還是看看以下大神級別的思路吧。
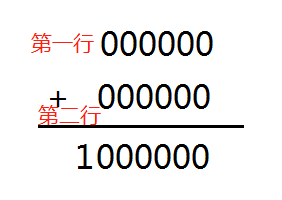
　　這道題我們應該理解為是要進行一種加法，和已經給定為n。然後我們現在有很多種2的k次方的值，要找出所有能加出n的方案。考慮到我們要加的數都是些2的k次方數，這其實跟二進位制的位數相加很像，每個硬幣都是二進位制位數上的一位，而且我們恰好不同種硬幣各有兩個，即有兩個2^0、兩個2^1、兩個2^2……把這些硬幣等分成兩份，正好就是兩個二進位制數，所以可以相當於兩個二進位制數數相加要得到n（大家自己看下圖悟一下）
　　

　　我們的硬幣等分成兩行，每一個硬幣都是每行上的一個0，因此這就是兩個長度為log2(n)的二進位制數的相加，和為長度為log2(n)+1的數且首位為1其餘位為0。
　　現在，再將上面圖中的兩行用十進位制的眼光來看，就是十進位制要加出個n總共有多少種組合方式，這個就是小學題了，比如n為8，有0+8，1+7，2+6，3+5，4+4。
　　走到這你就可以理解這份程式碼了，我們只需要注意兩點：
　　①、假如n為8，是允許如1000和000相加的情況的，也就是硬幣8和0（不拿）。
　　②、111+001（硬幣421和硬幣1）和101+011（硬幣41和硬幣21），只是前者選了第一行中面值為1的硬幣，後者選了第二行中面值為1的硬幣，本質上都得算同一種組合方法，也就是4211和4211都是同一種分法。因此我們可以考慮使用二進位制異或來對這種型別進行去重（這樣上0下1和上1下0結果都一樣了）。
　　結果都一樣後方案還是雙份的呀，怎麼變成一份呢。可以用set（注意這個容器）來儲存抑或結果，這樣就去重變成一份了。

程式碼

# include <iostream>
# include <set>

using namespace std;

int main(void) {
    int n;
    cin >> n;

    set<int> countset;
    for (int i = 0; i <= n/2; i++) {
        int result = i^(n-i); // 對兩行進行抑或 
        countset.insert(result);
    }
    cout <<  countset.size() << endl; 

    return
 
 0;
}