最短路徑演算法  -  迪傑斯特拉演算法

演算法描述 
1)演算法思想：設G=(V,E)是一個帶權有向圖，把圖中頂點集合V分成兩組，第一組為已求出最短路徑的頂點集合（用S表示，初始時S中只有一個源點，以後每求得一條最短路徑 , 就將加入到集合S中，直到全部頂點都加入到S中，演算法就結束了），第二組為其餘未確定最短路徑的頂點集合（用U表示），按最短路徑長度的遞增次序依次把第二組的頂點加入S中。在加入的過程中，總保持從源點v到S中各頂點的最短路徑長度不大於從源點v到U中任何頂點的最短路徑長度。此外，每個頂點對應一個距離，S中的頂點的距離就是從v到此頂點的最短路徑長度，U中的頂點的距離，是從v到此頂點只包括S中的頂點為中間頂點的當前最短路徑長度。

例子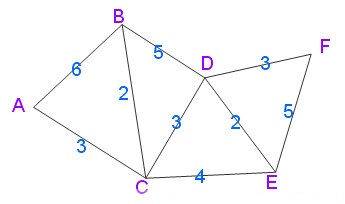 
 

 
重點需要理解：”按最短路徑長度的遞增次序依次把第二組的頂點加入S中。在加入的過程中，總保持從源點v到S中各頂點的最短路徑長度不大於從源點v到U中任何頂點的最短路徑長度”

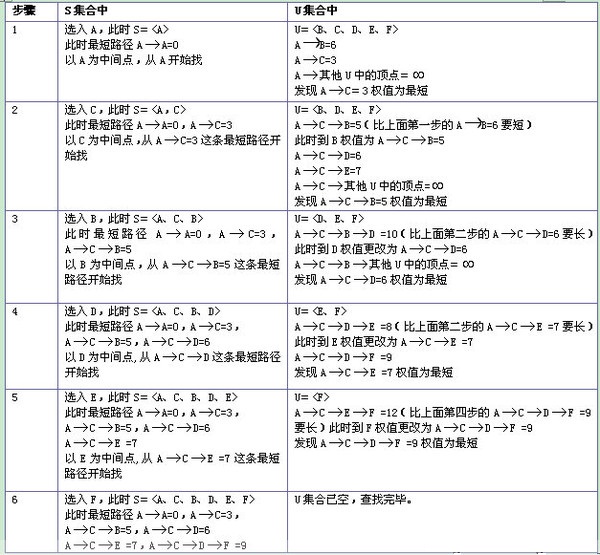
實際上，Dijkstra 演算法是一個排序過程，就上面的例子來說，是根據A到圖中其餘點的最短路徑長度進行排序，路徑越短越先被找到，路徑越長越靠後才能被找到，要找A到F的最短路徑，我們依次找到了 
A –> C 的最短路徑 3 
A –> C –> B 的最短路徑 5 
A –> C –> D 的最短路徑 6 
A –> C –> E 的最短路徑 7 
A –> C –> D –> F 的最短路徑 9 
Dijkstra 演算法執行的附加效果是得到了另一個資訊，A到C的路徑最短，其次是A到B, A到D, A到E, A到F