線段樹的定義

百度百科定義如下：

線段樹是一種二叉搜尋樹，與區間樹相似，它將一個區間劃分成一些單元區間，每個單元區間對應線段樹中的一個葉結點。

由定義可知，線段樹實質上是一種二叉搜尋樹，是一棵完全二叉樹，它們的各個節點儲存著一個線段的資訊(這個資訊可以是最值、區間和等多種資訊)。

線段樹的基本內容

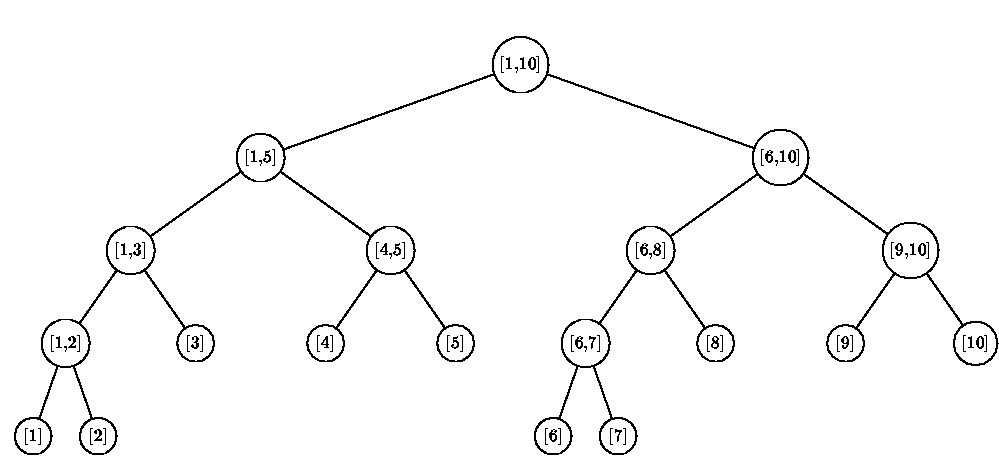
下圖是一棵區間長度為10的線段樹

一般的，我們把線段樹從上到下從左到右開始編號，例如：[1,10]編號為0，[1,5]編號為1，[6,10]編號為2，以此類推。其中每個非葉子節點都有左右兩棵子樹。

線段樹的儲存

//此存法為非指標版本
struct SEG{
    int
 
 l,r;//表示其所控制的區間(線段)
    int lch,rch;//表示它的左右兒子的節點編號
    int information;//表示儲存的資訊
    void clear(){//初始化
        l = r = 0;
        lch = rch = -1;//左右兒子為空
        information = INF;
    }
    void clear(int a,int b){//將其控制區間初始設為[a,b]
        clear();
        l = a;r = b;
    }
}Tree[MAXN*2];//MAXN為所需的最大值 可證明節點數最多為2倍區間長度
 

線段樹的基本操作

注意：這裡儲存的information是區間最小值

1.點修改

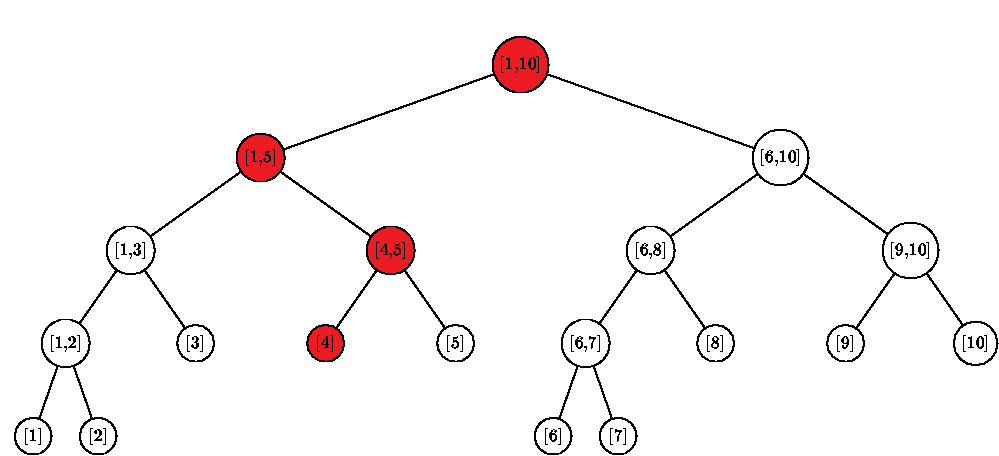
線段樹在點修改時會把包含該點的區間修改，下面是一個修改節點4的示意圖，紅色節點表示該節點被修改。具體改法詳見程式碼。

程式碼：

void change(int u,int p,int x){//u代表當前所在節點編號，p表示所要修改對應的線段，x是表示線段p要修改為x
    if(u==-1) return;//如果該節點不存在直接退出
    SEG &now=Tree[u];
    if(now.l>p||now.r<p) return;//如果p不在該區間內，則直接退出
 

    if(now.l==p&&now.r==p) now.min=x;//節點u為葉子節點，且節點u所管轄的線段正好是p，直接修改
    else{//此時滿足 l <= p <= r
        change(now.lch,p,x);//在左半個區間查詢並修改
        change(now.rch,p,x);//在右半個區間查詢並修改
        //修改完後依據其子區間的修改進行相應的修改
        now.min=min(Tree[now.lch].min,Tree[now.rch].min);
    }
}

其中單個點的修改時間是O(logn)。

2.查詢

還以上圖區間長度為10的線段樹為例，若要查詢區間[4,9]，那麼min([4,9])=min( min([4,5]) , min([6,8]) , min([9]) )，它可以分成這三個區間求最小值。
由此我們可以得出對於任意一個區間求最小值，其總可以分成線段樹上的幾個不同的節點求最小值（可證明分成的區間個數最多不超過2*h個，h為線段樹的深度），尋找的方法就是不斷的細分割槽間直到找到一個區間被所查詢的區間包括。具體實現見程式碼。

程式碼：

int query(int u,int L,int R){//u表示當前查詢已經訪問到節點u，要查詢的區間為L,R
    SEG &now=Tree[u];
    if(now.l>R||now.r<L) return INF;//如果所查詢的區間完全不在節點u所控制的區間範圍內返回正無窮
    if(now.l>=L&&now.r<=R) return now.min;//u所控制的區間是所要查詢的區間的子區間，則返回該區間的最小值
    return min(query(now.lch,L,R),query(now.rch,L,R));//如果上述兩種情況都不滿足則繼續細分割槽間直到滿足上述情況為止
}

同樣的每次查詢的時間為O(logn)。

3.建樹

建樹的過程是先預設好每個節點所管轄的線段，然後通過上面的change函式不斷的加點，預設每個點的函式見下面的程式碼。

預處理程式碼：

int tot=0;

int build(int L,int R){//需要建立一個區間為[L,R]的一棵線段樹
    int p=tot++;//申請一個新的節點
    SEG &now=Tree[p];
    now.clear(L,R);//並將該節點的區間設為[L,R]
    if(L<R){//如果區間還可以細分
        int mid=(L+R)/2;//取其中點繼續細分
        now.lch=build(L,mid);
        now.rch=build(mid+1,R);
        //並將其父節點的左右兒子設為其兒子的編號
    }
    return p;//返回該節點的編號
}

對於每個節點build函式只訪問了一次可以證明節點數最多為2*線段長度，因此上述的build函式的時間複雜度為O(n)。

建樹程式碼：

void Build(int n){
    build(1,n);//區間為[1,n]
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d",&x);
        change(0,i,x);
    }//對於每個節點不斷的加點並修改
}

對於每個節點的修改時間複雜度為O(logn)，因此總的建樹的程式碼時間複雜度應為O(nlogn)。

4.線段樹的區間修改

對於線段樹的區間修改，一種方法是按著點修改來這樣可以在O(nlogn)的時間內完成，但是時間效率並不高。因此我們介紹一個叫lazy_tag 的東西，通過對lazy_tag的修改來替代對區間的修改（注意當一個節點lazy_tag被修改後，它的影響範圍不只是侷限於該節點上，而是在對它本身為根的整棵子樹都有影響）。當我們訪問到一個節點時，如果其所儲存的lazy_tag值不為空，那麼就必須要把它所儲存的資訊傳到其孩子上（也就是下面的pushdown函式），原因見上面括號裡面的話。

注意：lazy_tag只是一個統稱在不同的程式碼裡面可能有不同的名字

程式碼：

void pushdown(int u){//注意此處的delta就是代表上面所說的lazy_tag
    if(u==-1) return;//寫上最好防止出現奇奇怪怪的錯誤QAQ
    SEG &now=Tree[u];
    if(now.delta){//如果lazy_tag不為空
        //注意此處全部用的是+=
        Tree[now.lch].delta+=now.delta;
        Tree[now.rch].delta+=now.delta;//修改lazy_tag
        Tree[now.lch].min+=now.delta;
        Tree[now.rch].min+=now.delta;//修改min
    }
    now.delta=0;//已經把lazy_tag傳下去，因此將其設為0
}

void Add(int u,int L,int R,int delta){
    if(u==-1) return;//沒錯，這也是防止一些奇奇怪怪的錯誤的QAQ
    SEG &now=Tree[u];
    if(now.l>R||now.r<L) return;//完全不包含的情況
    if(now.l>=L&&now.r<=R){//完全包含的情況
        //注意此處也是+= 
        now.min+=delta;
        now.delta+=delta;
        //然而我第一遍寫的時候順手寫了個等於然後就呵呵了QAQ
    }
    else{//部分包含的情況
        pushdown(u);//因為要遞迴呼叫它的子節點因此應該先把lazy_tag壓下去
        Add(now.lch,L,R,delta);
        Add(now.rch,L,R,delta);
        now.min=min(Tree[now.lch].min,Tree[now.rch].min);//子節點修改完後修改本身的值
    }
}
//因為區間修改完之後其查詢跟上面單點修改的查詢會有一點不一樣，故將查詢再次寫一遍
int query(int u,int L,int R){
    if(u==-1) return INF;
    SEG &now=Tree[u];
    if(now.l>R||now.r<L) return INF;
    if(now.l>=L&&now.r<=R) return now.min;
    else{
        pushdown(u);//注意其實就是這一點不一樣，還是剛剛說的在遞迴呼叫前必須先把lazy_tag壓到下面去，否則會出事的QAQ
        return min(query(now.lch,L,R),query(now.rch,L,R));
    }
}

舉個例子，還是上面的線段樹，當把區間[1,8]同時加上3時，會跟上面查詢時一樣，細分割槽間，分為[1,5]∪[6,8]，因此這兩條線段對應的節點上的lazy_tag的值增加（注意是增加不是變為）3，它所維護的資訊也因此而改變（例如min或max直接增加lazy_tag即可，而sum要增加（R-L+1）*lazy_tag）。

線段樹的模板題

這裡只提供兩道，一道是點修改：忠誠另一道是區間修改售票系統
這兩道一隻是檢驗最基本的線段樹的正確性，本文並沒有提供任何其他線段樹的用法，只介紹了一些最基本的東西。