關聯規則

參考資料：《資料探勘導論》人民郵電出版社Pang-Ning Tan等著

關聯規則是形如X→Y 的蘊含表示式，其中X和Y是不相交的項集。即X∩Y=∅。關聯規則的強度可以用它的支援度（support）和置信度（confidence）度量。支援度確定規則可以用於給定資料集的頻繁程度。而置信度確定Y在包含X的事務中出現的頻繁程度。

支援度

支援度是一種重要度量，因為支援度很低的規則可能只是偶然出現。從商務角度來看，低支援度的規則多半也是無意義的，因為對顧客很少同時購買的商品進行促銷可能好處也並不大。因此，支援度通常用來刪去哪些無意義的規則。此外，支援度還有一種期望的性質，可以用於關聯規則的有效發現。

置信度

置信度度量通過規則進行推理具有可靠性。對於給定的規則X→Y ，置信度越高，Y在包含X的事務中出現的可能性就越高。

應當小心解釋關聯規則分析的結果，由關聯規則作出的推論並不必然蘊含因果關係。它只表示規則前件和後件中的同時出現。

定義 關聯規則發現
給定事務的集合T，關聯規則發現是指找出支援度大於等於minsup並且置信度大於等於minconf的所有規則，其實minsup和minconf是對應的支援度和置信度閥值。

挖掘關聯規則的一種原始方法是，計算每個可能規則的支援度和置信度。但是這種方法的代價更高。提高關聯規則挖掘演算法效能的第一步是拆分支援度和置信度要求。

大部分關聯規則挖掘演算法通常採用的一種策略是，將關聯規則挖掘任務分解成如下2個子任務。
（1）頻繁項集產生：其目標是發現滿足最小支援度閥值的所有項集，這些項集稱作頻繁項集；
（2）規則的產生：其目標是從上一步發現的頻繁項集中提取所有高置信度的規則，這些規則稱作強規則。

通常，頻繁項集產生所需的計算開銷遠大於產生規則所需的開銷。

頻繁項集的產生

格結構常常用來列舉所有可能的項集。一般來說，一個包含k個項的資料集可能產生2k−1個頻繁項集（真子集）。
發現頻繁項集的一種原始方法是確定每個候選項集的支援度，這樣計算量是相當大的。
為了更加科學的計算頻繁項集，這裡先介紹下先驗原理。

先驗原理
如果一個項集是頻繁的，則它的所有子集一定也是頻繁的。
相反，如果一個項集是非頻繁的，則它的所有超集一定也是非頻繁的。

如果發現{a,b}是非頻繁的，則整個包含{a,b}超集的子圖可以被立即剪枝。這種基於支援度度量修剪指數搜尋空間的策略稱為基於支援度的剪枝。這種剪枝策略依賴於支援度度量的一個關鍵性質，即一個項集的支援度決不會超過它的子集的支援度。這種性質也稱為支援度度量的反單調性。

規則產生

如何有效的從給定的頻繁項集中提取關聯規則。
例子

設X={1，2，3}是頻繁項集。可以由X產生6個候選關聯規則：{1,2}→{3}，{1}→{2,3}….等。由於它們的支援度都等於X的支援度，這些規則一定滿足支援度閥值。
計算關聯規則的置信度並不需要再次掃描事務資料集。考慮規則{1,2}→{3}是由頻繁項集X={1,2,3}產生。該規則的置信度為σ({1,2,3})σ({1,2})。

基於置信度的剪枝

不像支援度度量。置信度不具有任何單調性。定理如下。

定理 如果規則X→Y−X不滿足置信度閥值，那麼X′→Y−X′的規則也一定不滿足置信度閥值。其中X′是 X的子集。

這一點通過定義很容易證明。

通過這一點性質可以進行剪枝。

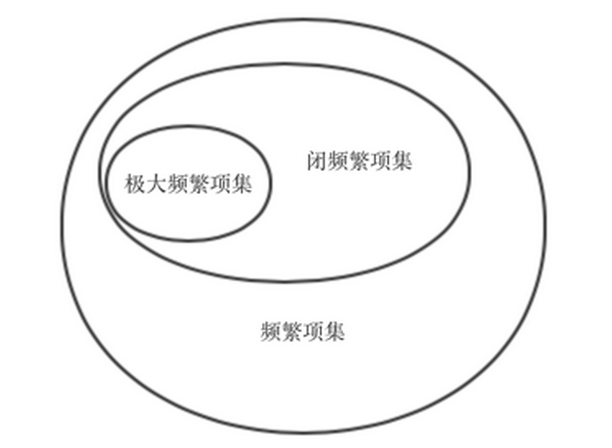
頻繁項集的緊湊表示

6.4.1 極大頻繁項集

定義 極大頻繁項集 ：極大頻繁項集是這樣的頻繁項集，它的直接超集都不是頻繁的。

6.4.2 閉頻繁項集

定義 閉項集 項集X是閉的，如果它的直接超集都不具備和他相同的支援度計數。
閉頻繁項集 一個項集是閉頻繁項集，如果它的閉的，並且它的支援度大於或等於最小支援度閥值。

6.6 FP增長演算法

該演算法不同於Apriori演算法的“產生-測試”範型，而是使用一種稱作FP樹的緊湊資料結構組織資料，並直接從該結構中提取頻繁項集。

6.6.1 FP樹表示法

詳見課本224頁
FP增長是一個有趣的演算法，它展示瞭如何使用事務資料集的壓縮表示來有效地產生頻繁項集。此外，對於某些事務資料集，FP增長演算法比標準Apriori演算法要快幾個數量級。FP增長演算法的執行效能依賴於資料集的壓縮因子。如果生成的條件FP樹非常茂盛，則演算法的效能顯著下降，因為演算法必須產生大量的子問題，並且需要合併每個子問題返回的結果。。。