Java多執行緒 -- JUC包原始碼分析18 -- ConcurrentSkipListMap(Set)/TreeMap(Set)/無鎖鏈表
-為什麼是SkipList,不是TreeMap的紅黑樹?
-無鎖鏈表的精髓
-ConcurrentSkipListMap
-ConcurrentSkipListSet
為什麼是SkipList?
大家都知道,在Java集合類中,有一個TreeMap,相對於HashMap,它的一個最大特點是:key是有序的。TreeMap的內部是用紅黑樹實現的。同HashMap一樣,它也是非執行緒安全的。
然後在JUC包中,提供了一個執行緒安全的、有序的HashMap,也就是今天所要講的ConcurrentSkipListMap。(關於什麼是SkipList,或者“跳躍表“,此處不再詳述,大家自行google之)
那為什麼實現這個執行緒安全的、有序的HashMap,不用紅黑樹,而用SkipList呢?
借用Doug Lea的原話:
The reason is that there are no known efficient lock-free insertion and deletion algorithms for search trees.也就是目前計算機領域沒找到一種高效的、作用在樹上的、無鎖的、增加和刪除結點的辦法。
那為什麼SkipList就可以無鎖的實現結點的增加、刪除呢?那就要從以下的故事說起:
無鎖鏈表
問題的提出
在Doug Lea的註釋中,他引用了下面這篇無鎖鏈表的Paper:
“A pragmatic implementation of non-blocking linked lists” (大家自行google之)
咋一看,無鎖鏈表不是很簡單嘛,還值得寫一篇paper專門論述?我們在前面講AQS的時候,已反覆用到無鎖佇列,其實現也是連結串列。那究竟區別在哪呢?
我們前面所講的無鎖佇列、棧,都是隻在頭、尾做cas操作,這個問題不大。而玄機就在,如果你在連結串列的中間做insert/delete操作,照通常的cas做法,就會出問題!
關於這個問題,那篇論文中有清晰的論述,此處引用如下:
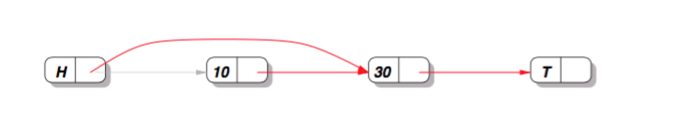
操作1: 在結點10後面插入結點20,沒什麼問題
操作2:刪除結點10,也沒什麼問題
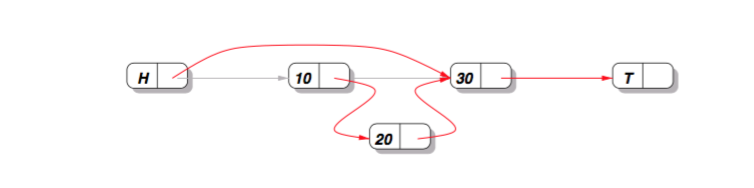
但如果2個執行緒同時操作,一個刪除結點10,一個要在10後面插入結點20。這2個操作都各自是CAS的,這個時候就會出問題:新插入的結點20會丟失!這個問題不是簡單的用CAS就可以解決的。
那為什麼會出現這個問題呢?
究其原因:我們在刪除結點10的時候,實際操作的是10的前驅H,10本身並沒有任何變化。這樣,在往10後插入20的這個執行緒,不知道10已經刪除了!!
要解決這個問題,論文中提出瞭如下的解決辦法:
把10的刪除分2步:第1步,把10的next指標,mark成刪除,也就是軟刪;第2步,找機會,物理刪除。
這個解決辦法有一個關鍵點:就是“把10的next指標指向20(insert操作)“ 和 “判斷10本身是否刪除“這2個,必須是原子的,必須在1個cas裡面完成!!!
解決辦法
辦法1: AtomicMarkableReference
要實現上面所說的,一個辦法是用前面所提到的AtomicMarkableReference,也就是說,每個next要是AtomicMarkableReference型別。但這個辦法,不夠高效。Doug Lea在ConcurrentSkipListMap的實現中,用了另外一種辦法
辦法2:Mark結點
* +——+ +——+ +——+ +——+
* … | b |——>| n |—–>|marker|——>| f | …
* +——+ +——+ +——+ +——+
*
* 3. CAS b’s next pointer over both n and its marker.
* From this point on, no new traversals will encounter n,
* and it can eventually be GCed.
* +——+ +——+
* … | b |———————————–>| f | …
* +——+ +——+
我們的目的,不就是想標記結點n,也就是標記它的next欄位嘛?那就新造一個marker結點,讓n.next = marker。
這樣也達到了,刪除n的時候,標記n的next指標的目的。
ConcurrentSkipListMap
SkipList結構
解決了無鎖鏈表的insert/delete問題,也就解決了SkipList的一個關鍵問題。因為SkipList,通俗點講,就是多層連結串列疊起來的:一個大的單向連結串列,儲存所有的
//最底層Node結點。所有的<k,v>對,都是這個單向連結串列串起來的。
static final class Node<K,V> {
final K key;
volatile Object value;
volatile Node<K,V> next;
。。。
}
//上面的Index層的結點
static class Index<K,V> {
final Node<K,V> node; //不儲存實際資料,指向Node
final Index<K,V> down; //關鍵點:每個Index結點,必須有個指標,指向其下一個Level對應的結點
volatile Index<K,V> right; //自己也組成單向連結串列
。。。
}
//整個ConcurrentSkipListMap就只用記錄最頂層的head結點
public class ConcurrentSkipListMap<K,V> extends AbstractMap<K,V>
implements ConcurrentNavigableMap<K,V>,
Cloneable,
java.io.Serializable {
。。。
private transient volatile HeadIndex<K,V> head;
}
final void initialize() {
keySet = null;
entrySet = null;
values = null;
descendingMap = null;
randomSeed = seedGenerator.nextInt() | 0x0100; // ensure nonzero
head = new HeadIndex<K,V>(new Node<K,V>(null, BASE_HEADER, null),
null, null, 1);
}put操作
public V put(K key, V value) {
if (value == null)
throw new NullPointerException();
return doPut(key, value, false);
}
private V doPut(K kkey, V value, boolean onlyIfAbsent) {
Comparable<? super K> key = comparable(kkey);
for (;;) {
Node<K,V> b = findPredecessor(key); //先找到結點的前驅(一定在base level上)
Node<K,V> n = b.next;
for (;;) {
if (n != null) {
Node<K,V> f = n.next;
if (n != b.next) // inconsistent read
break;
Object v = n.value;
if (v == null) { // n is deleted
n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // b is deleted
break;
int c = key.compareTo(n.key);
if (c > 0) {
b = n;
n = f;
continue;
}
if (c == 0) { //結點存在,直接改值
if (onlyIfAbsent || n.casValue(v, value))
return (V)v;
else
break; // restart if lost race to replace value
}
// else c < 0; fall through
}
Node<K,V> z = new Node<K,V>(kkey, value, n);
if (!b.casNext(n, z)) //結點不存在,新建一個,插入進入
break;
int level = randomLevel(); //關鍵點:判斷是否要給此結點加上Index層。randomLevel有50%概率會返回0,也就是說,50%的結點,不會有Index層,只會在最底層的連結串列上面
if (level > 0)
insertIndex(z, level); //level > 0,為其建索引
return null;
}
}
}
//關鍵函式:查詢一個結點的前驅,header開始,從左往右、從上往下遍歷
private Node<K,V> findPredecessor(Comparable<? super K> key) {
if (key == null)
throw new NullPointerException(); // don't postpone errors
for (;;) {
Index<K,V> q = head;
Index<K,V> r = q.right;
for (;;) {
if (r != null) {
Node<K,V> n = r.node;
K k = n.key;
if (n.value == null) {
if (!q.unlink(r))
break; // restart
r = q.right; // reread r
continue;
}
if (key.compareTo(k) > 0) {
q = r;
r = r.right;
continue;
}
}
Index<K,V> d = q.down; //跳到下一層
if (d != null) {
q = d;
r = d.right;
} else
return q.node;
}
}
}get操作
public V get(Object key) {
return doGet(key);
}
private V doGet(Object okey) {
Comparable<? super K> key = comparable(okey);
for (;;) {
Node<K,V> n = findNode(key);
if (n == null)
return null;
Object v = n.value;
if (v != null)
return (V)v;
}
}
private Node<K,V> findNode(Comparable<? super K> key) {
for (;;) {
Node<K,V> b = findPredecessor(key); //再次用的此函式
Node<K,V> n = b.next;
for (;;) {
if (n == null)
return null;
Node<K,V> f = n.next;
if (n != b.next) // inconsistent read
break;
Object v = n.value;
if (v == null) { // n is deleted
n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // b is deleted
break;
int c = key.compareTo(n.key);
if (c == 0)
return n;
if (c < 0)
return null;
b = n;
n = f;
}
}
}ConcurrentSkipListMap中,關於連結串列的操作,細節非常多,上面只是分析了其整體實現思路。關於insert/delete, insertIndex的具體實現細節,本文不在詳述,留待大家對照程式碼仔細分析。
ConcurrentSkipListSet
我們知道,TreeSet是基於TreeMap實現的,就是對TreeMap的一個簡單封裝。
同樣, ConcurrentSkipListSet也就是對ConcurrentSkipListMap的一個簡單封裝,具體不再詳述。
public ConcurrentSkipListSet() {
m = new ConcurrentSkipListMap<E,Object>();
}