題目描述：
在陣列中的兩個數字，如果前面一個數字大於後面的數字，則這兩個數字組成一個逆序對。輸入一個數組，求出這個陣列中的逆序對的總數。

輸入：
每個測試案例包括兩行：
第一行包含一個整數n，表示陣列中的元素個數。其中1 <= n <= 10^5。
第二行包含n個整數，每個陣列均為int型別。

輸出：
對應每個測試案例，輸出一個整數，表示陣列中的逆序對的總數。

樣例輸入：

4
7 5 6 4

樣例輸出：

5

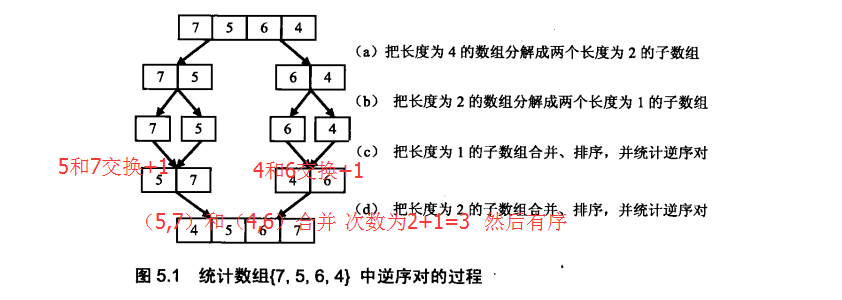
看到這樣的題目，最簡單的想法就是遍歷每一個元素，讓其與後面的元素對比，如果大於則count++，但是這樣的時間複雜度是o(n2)。這題有更好的解決方法，時間複雜度只需要o(nlogn)。其實這道題目的思路跟歸併排序差不多，求逆序對的過程就是一個求歸併排序的過程，在求出逆序對以後，原陣列變得有序，是通過歸併排序得到的。

考慮一下，逆序是說a[i]>a[j]，j>i。那麼在排序的過程中，會把a[i]和a[j]交換過來，這個交換的過程，每交換一次，就是一個逆序對的“正序”過程。歸併排序的思想就是把前一段排序，後一段排序，然後再整體排序。利用歸併排序的過程中，在每一次歸併兩個陣列的時候，如果左陣列比右陣列大，那麼著就是一個逆序。記錄所有左陣列比右陣列大的情況，就是全部的逆序數目。

package Test;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import
 
 java.io.StreamTokenizer;

public class jobdu1348 {
    static long count = 0;
    public static void mergeSort(int []input,int left,int right){
        //分治
        int mid = (left + right) / 2;  
        if (left < right) {  
            // 左邊  
            mergeSort(input,left,mid);  
            // 右邊  
 

            mergeSort(input,mid+1,right);  
            // 左右歸併  
            merge(input,left,mid,right);  
        }  
    }
    /**
     * 二路歸併
     * @param input
     * @param left左陣列的第一個元素的索引
     * @param center左陣列的最後一個元素的索引，center+1是右陣列第一個元素的索引
     * @param right右陣列最後一個元素的索引
     */
    public static void merge(int[]input,int left,int center,int right){
        int []tempArray = new int[right-left+1];
        int mid = center+1;
        int temp = left;
        int current = 0;
        while(left<=center && mid<=right){
            if(input[left]>input[mid]){
                tempArray[current++]=input[mid++];
                /*
                 * 如果input[left]>input[mid]，那麼表明下標為left~center的值都會比input[mid]大;
                 * (5,7,8)(4,9)合併為 3+0+0+0
                 * */               
                count+=center-left+1;
            }else{
                tempArray[current++]=input[left++];
            }
        }
        //只會執行一個
        while(left<=center){
            tempArray[current++]=input[left++];
        }
        while(mid<=right){
            tempArray[current++]=input[mid++];
        }
        current=0;
        while(temp<=right){
            input[temp++]=tempArray[current++];
        }
    }
    public static void main(String[] args) throws IOException {
        StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        while(cin.nextToken()!=cin.TT_EOF){
            int n = (int)cin.nval;
            int []input = new int[n];
            for(int i=0;i<n;i++){
                cin.nextToken();
                input[i] = (int)cin.nval;
            }
            count=0;
            mergeSort(input,0,input.length-1);
            System.out.println(count);
        }
    }
}