排序演算法是演算法的入門知識，其經典思想可以用於很多演算法當中。因為其實現程式碼較短，應用較常見。所以在面試中經常會問到排序演算法及其相關的問題。但萬變不離其宗，只要熟悉了思想，靈活運用也不是難事。一般在面試中最常考的是快速排序和歸併排序，並且經常有面試官要求現場寫出這兩種排序的程式碼。對這兩種排序的程式碼一定要信手拈來才行。還有插入排序、氣泡排序、堆排序、選擇排序、基數排序、桶排序等。面試官對於這些排序可能會要求比較各自的優劣、各種演算法的思想及其使用場景。還有要會分析演算法的時間和空間複雜度。通常查詢和排序演算法的考察是面試的開始，如果這些問題回答不好，估計面試官都沒有繼續面試下去的興趣都沒了。所以想開個好頭就要把常見的排序演算法思想及其特點要熟練掌握，有必要熟練寫出程式碼[1]。

對排序演算法的分類方式也有很多種[2]:

1、計算的時間複雜度（最差、平均、和最好效能），依據列表（list）的大小(n)。一般而言，好的效能是O(n log n)，壞的效能是O(n2)。對於一個排序理想的效能是O(n)，但平均而言不可能達到。基於比較的排序演算法對大多數輸入而言至少需要O(n log n)。

2、空間複雜度。

3、穩定性：穩定排序演算法會讓原本有相等鍵值的紀錄維持相對次序。也就是如果一個排序演算法是穩定的，當有兩個相等鍵值的紀錄R和S，且在原本的列表中R出現在S之前，在排序過的列表中R也將會是在S之前。

4、排序的方法：交換、選擇、插入、合併等等。

首先給出一個對比的表格，以便從整體上理解排序演算法：

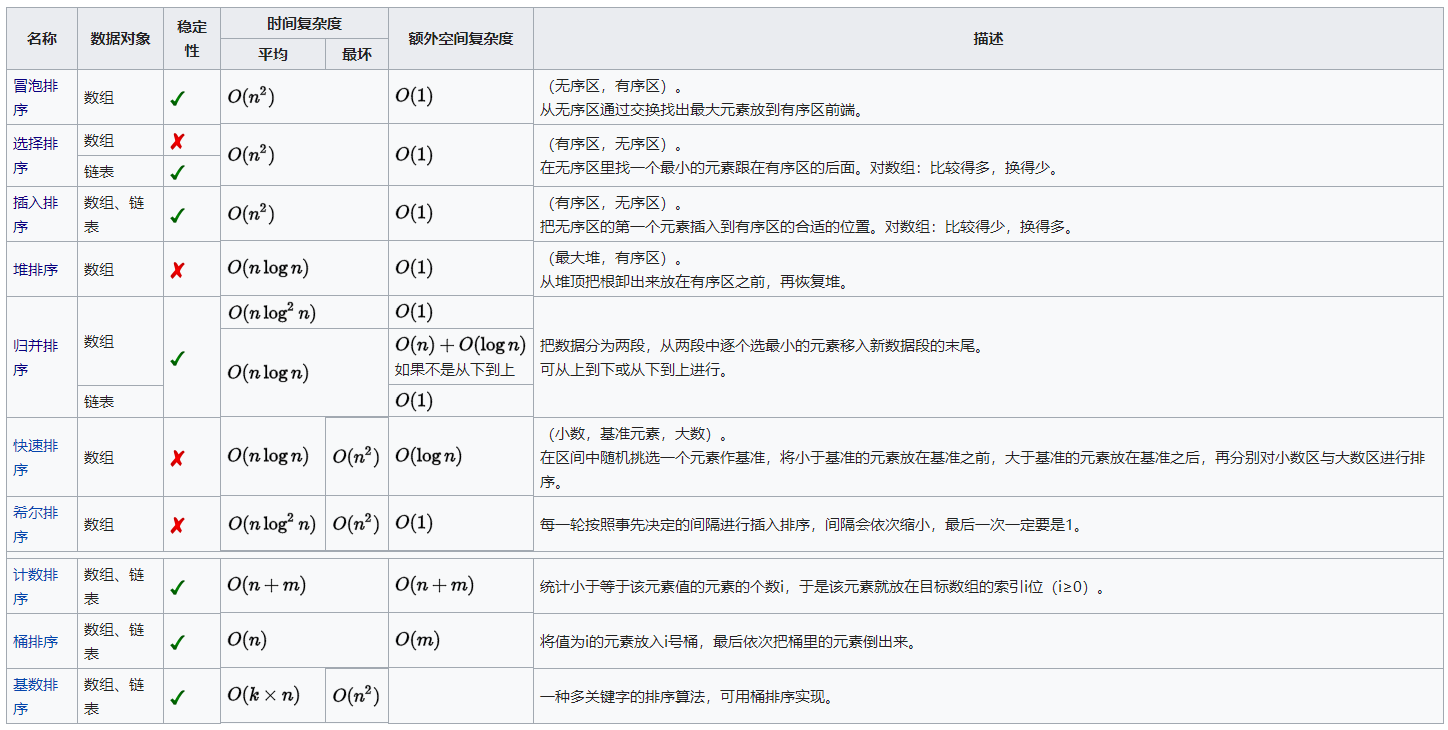
接下來我們按照

交換排序：氣泡排序、快速排序

選擇排序：選擇排序、堆排序

插入排序：插入排序

歸併排序：歸併排序

的順序、分析一下這六種常見的排序演算法及其使用場景。限於篇幅，某些演算法的詳細演示和圖示請在演算法導論中尋找詳細的參考。值得一提的是，本文中的程式碼思想都源自演算法導論，如果有不明白的程式碼請翻閱演算法導論一書。本文專為面試前突擊而作，套路和思想和演算法導論一模一樣，即以方便記憶為主。

交換排序

交換排序的基本方法是在待排序的元素中選擇兩個元素，將他們的值進行比較，如果反序則交換他們的位置，直到沒有反序的記錄為止。交換排序中常見的是氣泡排序和快速排序。

氣泡排序

氣泡排序演算法的虛擬碼如下：

function bubble_sort (array, length) {
    var i, j;
    for(i from 0 to length-1){
        for(j from 0 to length-1-i){
            if (array[j] > array[j+1])
                swap(array[j], array[j+1])
        }
    }
}

參考虛擬碼不難寫出程式碼：

 /**
 * @param arr
 * 1、氣泡排序
 * 氣泡排序時間複雜度O(n^2)，比較次數多，交換次數多。因此是效率極低的演算法。
 * 氣泡排序是一種穩定的演算法。
 */
public static void bubbleSort(int[] arr){ 
    int len = arr.length;
    for(int i = 0; i < len - 1; i++){
        for(int j = 0; j < len - 1 - i; j++){
            if(arr[j] > arr[j + 1]){
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }

} 

氣泡排序對n個專案需要O(n^2)的比較次數，且可以原地排序。儘管這個演算法是最簡單瞭解和實現的排序演算法之一，但氣泡排序的實現通常會對已經排序好的數列拙劣地執行O(n^2),它對於包含大量的元素的數列排序是很沒有效率的。

快速排序

快速排序是氣泡排序的一種改進，氣泡排序排完一趟是最大值冒出來了，那麼可不可以先選定一個值，然後掃描待排序序列，把小於該值的記錄和大於該值的記錄分成兩個單獨的序列，然後分別對這兩個序列進行上述操作。這就是快速排序，我們把選定的那個值稱為樞紐值，如果樞紐值為序列中的最大值，那麼一趟快速排序就變成了一趟氣泡排序。

快速排序是基於分治模式的[3]：

分解：陣列A【p..r】被劃分成兩個（可能空）子陣列A【p..q-1】和A【q+1..r】，使得A【p..q-1】中的每個元素都小於等於A(q)，而且，小於等於A【q+1..r】中的元素。下 標q 也在返個劃分過程中迕行計算。

解決：通過遞迴呼叫快速排序，對子陣列A【p..q-1】和A【q+1..r】排序。

合併：因為兩個子陣列使就地排序的，將它們的合併不需要操作：整個陣列A【p..r】已排序。

/**
 * @param arr
 * @param p
 * @param r
 * 2、快排
 * 快排最壞時間複雜度O(n^2)，平均時間複雜度O(nlgn)。空間複雜度為O(nlgn)。
 * 快排是一種不穩定的演算法。
 */
public static void quickSort(int[] arr, int p, int r){
    if(p < r){
        int q = partition(arr, p, r);
        quickSort(arr, p, q - 1);
        quickSort(arr, q + 1, r);

    }
    return;
}

public static int partition(int[] arr, int p, int r){
    int x = arr[r];
    int i = p - 1;
    for(int j = p; j < r; j++){
        if(arr[j] < x){
            swap(arr, ++i, j);
        }
    }
    swap(arr, ++i, r);
    return i;
}

private static void swap(int[] arr, int i,int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

快速排序是最常用的一種排序演算法，包括C的qsort，C++和Java的sort，都採用了快排（C++和Java的sort經過了優化，還混合了其他排序演算法）。

快排最壞情況O( n^2 )，但平均效率O(n lg n)，而且這個O(n lg n)幾號中隱含的常數因子很小，快排可以說是最快的排序演算法，並非浪得虛名。另外它還是就地排序。

舉一個例子，java中arrays.sort()方法：

1）當待排序的陣列中的元素個數較少時，原始碼中的閥值為7，採用的是插入排序。儘管插入排序的時間複雜度為0(n^2)，但是當陣列元素較少時，插入排序優於快速排序，因為這時快速排序的遞迴操作影響效能。

2）較好的選擇了劃分元（基準元素）。能夠將陣列分成大致兩個相等的部分，避免出現最壞的情況。例如當陣列有序的的情況下，選擇第一個元素作為劃分元，將使得演算法的時間複雜度達到O(n^2).

　原始碼中選擇劃分元的方法:

　　當陣列大小為 size=7 時 ，取陣列中間元素作為劃分元。int n=m>>1;(此方法值得借鑑)

　　當陣列大小 7

選擇排序

選擇排序的基本思想是，每趟排序在待排序序列中，選擇值較小的元素，順序新增到有序序列的最後，直到全部記錄排序完畢。常用的有簡單選擇排序和堆排序。

簡單選擇排序

簡單選擇排序是一種簡單直觀的排序演算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然後，再從剩餘未排序元素中繼續尋找最小（大）元素，然後放到已排序序列的末尾。以此類推，直到所有元素均排序完畢。

/**
 * @param arr
 * 3、選擇排序
 * 選擇排序時間複雜度O(n^2)。比較次數多，交換次數少。
 * 選擇排序是一種不穩定的排序演算法。例如:(7) 2 5 9 3 4 [7] 1...
 * 當我們利用直接選擇排序演算法進行排序時,(7)和1調換,(7)就在[7]的後面了,原來的次序改變,這樣就不穩定.
 */
public static void selectSort(int[] arr){
    int len = arr.length;
    for(int i = 0; i < len - 1; i++){
        int min = i;
        for(int j = i + 1; j < len; j ++){
            if(arr[min] > arr[j]){
                min = j;
            }
        }
        swap(arr, i, min);
    }
}

簡單選擇排序是移動次數最少的演算法。原始序列為正序時，比較次數O( n^2 )，移動次數為0；逆序時，比較次數O( n^2 )，移動次數O( n )。平均情況下時間複雜度O( n^2 )，空間複雜度O( 1 )。

另外簡單選擇排序是不穩定的；簡單選擇排序是原地排序。

堆排序

在堆的資料結構中，堆中的最大值總是位於根節點(在優先佇列中使用堆的話堆中的最小值位於根節點)。堆排序需要用到堆中定義以下三個種操作：

1. 最大堆調整（Max_Heapify）：將堆的末端子節點作調整，使得子節點永遠小於父節點。
2. 建立最大堆（Build_Max_Heap）：將堆所有資料重新排序。
3. 堆排序（HeapSort）：移除位在第一個資料的根節點，並做最大堆調整的遞迴運算。

/**
         * @param arr
         * 4、堆排序
         * 堆排序有三個操作：1、維護堆性質；2、建堆；3、堆排序
         * 1、維護堆性質，時間複雜度為O(lgn)
         * 2、建堆，時間複雜度O(n)
         * 3、堆排序，n-1次呼叫維護堆性質函式，每次時間複雜度為O(lgn)，因此總體時間複雜度為O(nlgn)。
         * 空間複雜度為O(lgn)
         * 堆排序是一種不穩定的排序。
         */
        public static void heapSort(int[] arr){
            /*
             *  第一步：將陣列堆化
             *  beginIndex = 第一個非葉子節點。
             *  從第一個非葉子節點開始即可。無需從最後一個葉子節點開始。
             *  葉子節點可以看作已符合堆要求的節點，根節點就是它自己且自己以下值為最大。
             */
            int len = arr.length - 1;
            int beginIndex = (len - 1) >> 1; 
            for(int i = beginIndex; i >= 0; i--){
                maxHeapify(arr, i, len);
            }

            /*
             * 第二步：對堆化資料排序
             * 每次都是移出最頂層的根節點A[0]，與最尾部節點位置調換，同時遍歷長度 - 1。
             * 然後從新整理被換到根節點的末尾元素，使其符合堆的特性。
             * 直至未排序的堆長度為 0。
             */
            for(int i = len; i > 0; i--){
                swap(arr, 0, i);
                maxHeapify(arr, 0, i - 1);
            }
        }


        /**
         * 調整索引為 index 處的資料，使其符合堆的特性。
         * 
         * @param index 需要堆化處理的資料的索引
         * @param len 未排序的堆（陣列）的長度
         */
        public static void maxHeapify(int[] arr, int i, int len){
            int l = 2 * i + 1;              // 左子節點索引
            int r = l + 1;                  // 右子節點索引
            int largest = i;                // 預設父節點索引為最大值索引
            if(l <= len && arr[l] > arr[i]){        //判斷左子節點是否比父節點大
                largest = l;
            }
            if(r <= len && arr[r] > arr[largest]){              //判斷右子節點是否比父節點大
                largest = r;
            }
            if(largest != i){
                swap(arr, i, largest);              // 如果父節點被子節點調換，
                maxHeapify(arr, largest, len);              // 則需要繼續判斷換下後的父節點是否符合堆的特性。
            }
        }

插入排序

插入排序不是通過交換位置，而是通過比較找到合適的位置插入元素。類似於打撲克牌，整牌的時候就是拿到一張牌，找到一個合適的位置插入。這個原理其實和插入排序是一樣的。

直接插入排序

/**
 * @param arr
 * 5、插入排序
 * 插入排序平均時間複雜度為O(n^2)，空間複雜度為O(1)。
 * 直接插入排序是一種穩定的演算法，當陣列長度較小時，效果要比快排好。
 */
public static void insertSort(int[] arr){
    int len = arr.length;
    for(int i = 1; i < len; i++){
        int temp = arr[i];
        int j = i - 1;
        // 找到合適的位置j來插入arr[i]
        while(j >= 0 && arr[j] > temp){
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = temp;
    }
}

合併排序

合併排序的基本方法是，將兩個或兩個以上的有序序列歸併成一個有序序列。常見的演算法有歸併排序。

歸併排序

/**
         * @param arr
         * 6、歸併排序
         * 歸併排序平均時間複雜度為O(nlgn)，空間複雜度為O(n)。
         * 歸併排序是一種穩定的演算法。
         * 
         */
        public static void mergeSort(int[] arr, int p, int r){
            if (p < r){
                int q = (p + r) / 2;
                mergeSort(arr, p, q);
                mergeSort(arr, q + 1, r);
                merge(arr, p, q, r);
            }

        }

        public static void merge(int[] arr, int p, int q, int r){
            int len1 = q - p + 1;
            int len2 = r - q;
            // 建立長度為len1和len2的新陣列。
            int[] arr1 = new int[len1 + 1];
            int[] arr2 = new int[len2 + 1];
            // 賦值，尾部值為無窮。
            for(int i = 0; i < len1; i++){
                arr1[i] = arr[p + i];
            }
            for(int i = 0; i < len2; i++){
                arr2[i] = arr[q + 1 + i];
            }
            arr1[len1] = Integer.MAX_VALUE;
            arr2[len2] = Integer.MAX_VALUE;
            // 比較兩個新陣列的元素大小，將小的元素新增的arr，進行排序。
            for(int k = 0, i = 0, j = 0; k < len1 + len2; k++){
                if(arr1[i] < arr2[j]){
                    arr[p + k] = arr1[i++];
                }else{
                    arr[p + k] = arr2[j++];
                }

            }
        }

參考文獻

[3] 演算法導論