1 過擬合原因

（1）建模樣本抽取錯誤，包括（但不限於）樣本數量太少，抽樣方法錯誤， 抽樣時沒有足夠正確考慮業務場景或業務特點，不能有效足夠代表業務邏輯或業務場景。

（2）樣本里的噪音資料干擾過大，模型學習了噪音特徵，反而忽略了真實的輸入輸出間的關係。

（3）建模時的“邏輯假設”到了模型應用時已經不能成立了。 任何預測模型都是在假設的基礎上才可以搭建和應用的。常用的假設包括：

• 假設歷史資料可以推測未來，
• 假設業務環節沒有發生顯著變化，
• 假設建模資料與後來的應用資料是相似的，等等。
• 如果上述假設違反了業務場景的話，根據這些假設搭建的模型當然是無法有效應用的。

（4）引數太多、模型複雜度高。

（5）決策樹模型。

• 如果我們對於決策樹的生長沒有合理的限制和修剪的話， 決策樹的自由生長有可能每片葉子裡只包含單純的事件資料(event)或非事件資料（no event）， 可以想象，這種決策樹當然可以完美匹配（擬合）訓練資料， 但是一旦應用到新的業務真實資料時，效果是一塌糊塗。

（6）神經網路模型。

• 由於對樣本資料,可能存在隱單元的表示不唯一，即產生的分類的決策面不唯一，隨著學習的進行, BP演算法使權值可能收斂過於複雜的決策面，並至極致。
• 權值學習迭代次數足夠多(Overtraining)，擬合了訓練資料中的噪聲和訓練樣例中沒有代表性的特徵.

2 判斷是否過擬合

• 首先看一下三種誤差的計算方法：
  training error (訓練誤差)
  $J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$
  cross validation error (交叉驗證誤差)
  $J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum_{i=1}^{m_{cv}}(h_\theta(x_{cv}^{(i)})-y_{cv}^{(i)})^2$
  
  test error (測試誤差)
  $J_{test}(\theta) = \frac{1}{2m_{test}}\sum_{i=1}^{m_{test}}(h_\theta(x_{test}^{(i)})-y_{test}^{(i)})^2$
• 判斷究模型否過擬合方法：

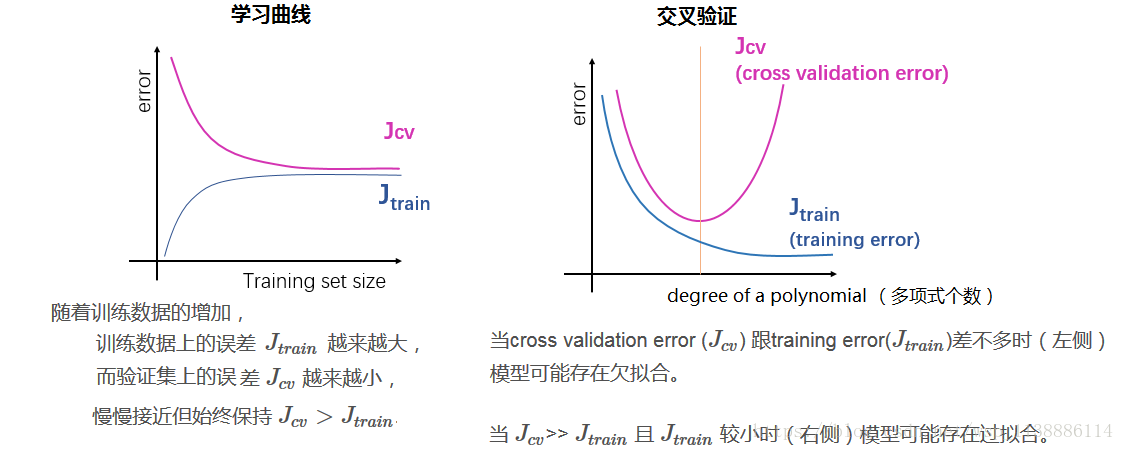
1）學習曲線（learning curves）

學習曲線就是比較 $j_{train}$ 和 $j_{cv}$。

如下圖所示，為一般的學習曲線，藍線:訓練誤差 $j_{train}$ , 粉色的線:驗證集上的誤差 $j_{cv}$，橫軸表示訓練集合的大小。

2）交叉驗證（cross-validation）

模型的Error = Bias + Variance
Error反映的是整個模型的準確度
Bias反映的是模型在樣本上的輸出與真實值之間的誤差，即模型本身的精準度
Variance反映的是模型每一次輸出結果與模型輸出期望之間的誤差，即模型的穩定性。

3 欠擬合–解決方法

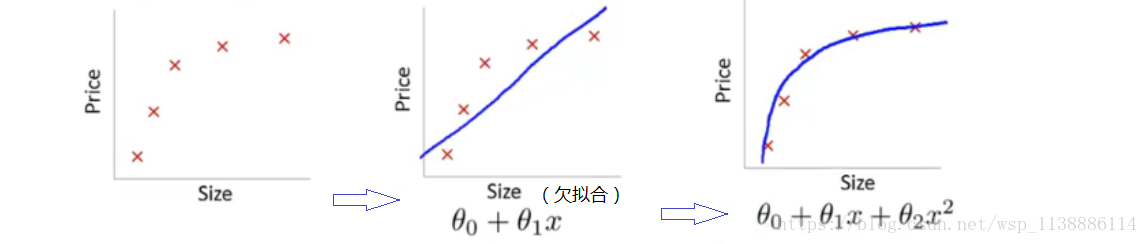
首先欠擬合就是模型沒有很好地捕捉到資料特徵，不能夠很好地擬合數據。

解決方法：

1. 新增其他特徵項，模型出現欠擬合的時候是因為特徵項不夠導致的，可以新增其他特徵項來很好地解決。
   例如，“組合”、“泛化”、“相關性”三類特徵是特徵新增的重要手段， 無論在什麼場景，都可以照葫蘆畫瓢，總會得到意想不到的效果。 除上面的特徵之外，“上下文特徵”、“平臺特徵”等等，都可以作為特徵新增的首選項。

2. 新增多項式特徵，例如將線性模型通過新增二次項或者三次項使模型泛化能力更強。

3. 減少正則化引數，正則化的目的是用來防止過擬合的，當模型出現了欠擬合，則需要減少正則化引數。

4 過擬合–解決方法

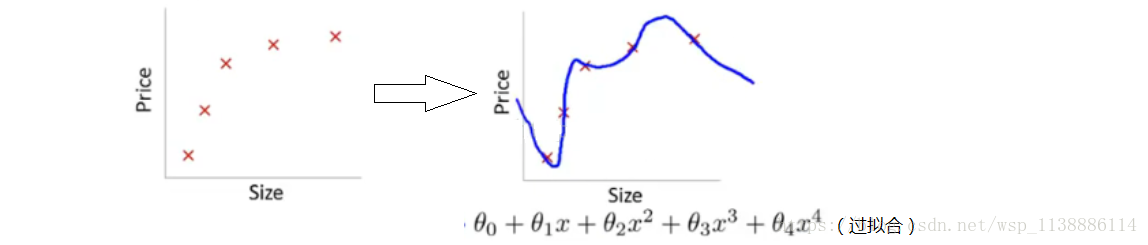
通俗一點地來說過擬合就是模型把資料學習的太徹底(強行擬合)，以至於把噪聲資料的特徵也學習到了， 這樣不能夠很好的分離（識別）測試資料，模型泛化能力太差。例如下面的例子：

解決方法：

1. 重新清洗資料，導致過擬合的一個原因也有可能是資料不純導致的， 如果出現了過擬合就需要我們重新清洗資料。

2. 增大資料的訓練量，之前用於訓練的資料量太小導致的，訓練資料佔總資料的比例過小。

3. 採用正則化方法。正則化方法包括 L0正則、L1正則和L2正則， 而正則一般是在目標函式之後加上對於的範數。但是在機器學習中一般使用L2正則，下面看具體的原因。

   1. L0 範數是指向量中非0的元素的個數。

   2. L1 範數是指向量中各個元素絕對值之和，也叫“稀疏規則運算元”（Lasso regularization）。
      兩者都可以實現稀疏性，既然L0可以實現稀疏，為什麼不用L0，而要用L1呢？個人理解一是因為L0範數很難優化求解（NP難問題）， 兩者都可以實現稀疏性，既然L0可以實現稀疏，為什麼不用L0，而要用L1呢？個人理解一是因為L0範數很難優化求解（NP難問題）， 二是L1範數是L0範數的最優凸近似，而且它比L0範數要容易優化求解。

   3. L2 範數是指向量各元素的平方和然後求平方根。
      可以使得W的每個元素都很小，都接近於0， 可以使得W的每個元素都很小，都接近於0， 但與L1範數不同，它不會讓它等於0，而是接近於0。L2正則項起到使得引數w變小加劇的效果，
      但是為什麼可以防止過擬合呢？一個通俗的理解便是：更小的引數值w意味著模型的複雜度更低， 對訓練資料的擬合剛剛好（奧卡姆剃刀），不會過分擬合訓練資料，從而使得不會過擬合， 以提高模型的泛化能力。還有就是看到有人說L2範數有助於處理 condition number不好的 情況下矩陣求逆很困難的問題（具體這兒我也不是太理解）。

5 神經網路過擬合解決方案

（1）權值衰減.它在每次迭代過程中以某個小因子降低每個權值,這等效於修改E的定義,  
加入一個與網路權值的總量相應的懲罰項,此方法的動機是保持權值較小,避免weight decay, 從而使學習過程向著複雜決策面的反方向偏。 

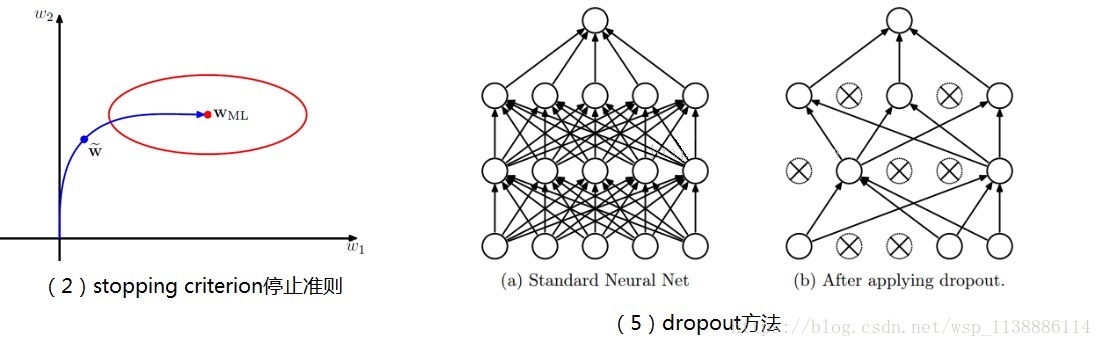
（2）適當的stopping criterion （如圖）
    在二次誤差函式的情況下，關於早停止和權值衰減類似結果的原因說明。 
    橢圓給出了常數誤差函式的輪廓線，Wml表示誤差函式的最小值。 
    如果權向量的起始點為原點，按照區域性負梯度的方向移動，那麼它會沿著曲線給出的路徑移動。 
    通過對訓練過程早停止，我們找到了一個權值向量w。 
    定性地說，它類似於使用檢點的權值衰減正則化項，然後最小化正則化誤差函式的方法得到的權值。  

（3）驗證資料
	一個最成功的方法是在訓練資料外再為演算法提供一套驗證資料,
	應該使用在驗證集合上產生最小誤差的迭代次數,不是總能明顯地確定驗證集合何時達到最小誤差. 
	（通常30%的訓練模式；每個時期檢查驗證集錯誤；如果驗證錯誤上升，停止訓練）  
	
（4）交叉驗證
	交叉驗證方法在可獲得額外的資料提供驗證集合時工作得很好,但是小訓練集合的過度擬合問題更為嚴重.   
	
（5）採用dropout方法。這個方法在神經網路裡面很常用。 
	dropout方法是ImageNet中提出的一種方法，通俗一點講就是dropout方法在訓練的時候讓神經元以一定的概率不工作，如下圖。