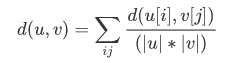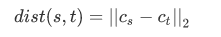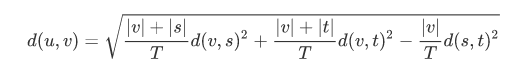Python層次聚類sci.cluster.hierarchy.linkage函式詳解
1 函式原型:
scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)函式功能:進行層次聚類/凝聚聚類。
引數:
y: 可以是1維壓縮向量(距離向量),也可以是2維觀測向量(座標矩陣)。若y是1維壓縮向量,則y必須是n個初始觀測值的組合,n是座標矩陣中成對的觀測值。
返回值:(n-1)*4的矩陣Z(後面會仔細的講解返回值各個欄位的含義)
linkage方法用於計算兩個聚類簇s和t之間的距離d(s,t),這個方法的使用在層次聚類之前。當s和t行程一個新的聚類簇u時,s和t被從森林(已經形成的聚類簇群)中移除,而用新的聚類簇u來代替。當森林中只有一個聚類簇時演算法停止。而這個聚類簇就成了聚類樹的根。
距離矩陣在每次迭代中都將被儲存,d[i,j]對應於第i個聚類簇與第j個聚類簇之間的距離。每次迭代必須更新新形成的聚類簇之間的距離矩陣。
假定現在有|u|個初始觀測值u[0],...,u[|u|-1]在聚類簇u中,有|v|個初始物件v[0],...,v[|v|-1]在聚類簇v中。回憶s和t合併成u。讓v成為森林中的聚類簇,而不是u。
下面是計算新形成的聚類簇u和v之間距離的方法:
- method = ‘single’
d(u,v) = min(dist(u[i],u[j]))
對於u中所有點i和v中所有點j。這被稱為最近鄰點演算法。
- method = 'complete'
d(u,v) = max(dist(u[i],u[j]))
對於u中所有點i和v中所有點j。這被稱為最近鄰點演算法。
- method = 'average'
|u|,|v|是聚類u和v中元素的的個數,這被稱為UPGMA演算法(非加權組平均)法。
- method = 'weighted'
d(u,v) = (dist(s,v) + dist(t,v))/2
u是由s和t形成的,而v是森林中剩餘的聚類簇,這被稱為WPGMA(加權分組平均)法。
- method = 'centroid'
Cs和Ct分別為聚類簇s和t的聚類中心,當s和t形成一個新的聚類簇時,聚類中心centroid會在s和t上重新計算。這段聚類就變成了u的質心和剩下聚類簇v的質心之間的歐式距離。這杯稱為UPGMC演算法(採用質心的無加權paire-group方法)。
- method = 'median'
- method = 'ward' (沃德方差最小化演算法)
新的輸入d(u,v)通過下式計算得出,
u是s和t組成的新的聚類,v是森林中未使用的聚類。T = |v|+|s|+|t|,|*|是聚類簇中觀測值的個數。
注意:當最小距離在一個森林中成對存在時,即有多個最小距離的時候,具體的實現要看MATLAB的版本(因為這個函式是從matlab裡面copy過來的)。
2 引數:
y:nump.ndarry。是一個壓縮距離的平面上三角矩陣。或者n*m的觀測值。壓縮距離矩陣的所有元素必須是有限的,沒有NaNs或infs。
method:str,可選。
metric:str或function,可選。在y維觀測向量的情況下使用該引數,苟澤忽略。參照有效距離度量列表的pdist函式,還可以使用自定義距離函式。
optimal_ordering:bool。若為true,linkage矩陣則被重新排序,以便連續葉子間距最小。當資料視覺化時,這將使得樹結構更為直觀。預設為false,因為資料集非常大時,執行此操作計算量將非常大。
Note:上述演算法的時間複雜度如下:
| 演算法 | 時間複雜度 |
| single | O(n2) |
| complete | O(n2) |
| average | O(n2) |
| weighted | O(n2) |
| ward | O(n2) |
| 其他 | O(n2) |
3 返回值:
Z:numpy.ndarry。
層次聚類編碼為一個linkage矩陣。
Z共有四列組成,第一欄位與第二欄位分別為聚類簇的編號,在初始距離前每個初始值被從0~n-1進行標識,每生成一個新的聚類簇就在此基礎上增加一對新的聚類簇進行標識,第三個欄位表示前兩個聚類簇之間的距離,第四個欄位表示新生成聚類簇所包含的元素的個數。
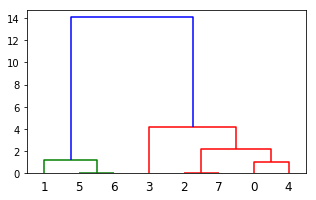
下面舉個例子來說明一下:
#%%
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
# X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
plt.show()下面是返回值的解析:
2018/2/25凌晨1點於中關村。