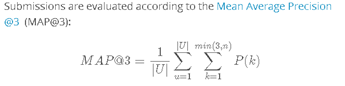這是參加的第二個kaggle的比賽：facebook V：Predicting Check ins，其與前一陣子Expedia比賽很相似，其預測目標集合都是非常大的。這是比賽入口：https://www.kaggle.com/c/facebook-v-predicting-check-ins。本文可以當做一個簡單粗糙的資料探勘tutorial。

1、關於賽題

比賽題目要求是預測登入使用者的地點id，資料集是10km * 10km的方形區域（facebook團隊創造的虛擬人工世界）中100,000個地點id的使用者相關資訊，其中的資料帶有程度不定的噪聲。提交的檔案要求預測test.csv中每一個row_id（8,607,230 個）對應的地點id預測，選手可為每個row_id提供三個預測地點。結果的評估公式如下：

如上所示，評估的公式採用MAP公式，即要求推薦的三個place_id 中沒有一個預測正確則不得分。在三個place_id中，有次序關係，若預測正確的place_id次序越前，則得分越高。

2、資料探索

2.1 資料概況：

在對於該資料探勘問題的方案制定前，需要先對資料進行探索。資料探索有助於對資料有個初步的瞭解。其中訓練資料為1.24G、測試資料為0.27G。機器為8G RAM。故將訓練資料資料抽取10,000,000個樣本讀入記憶體，瞭解其概況資訊。

import numpy as np
import pandas as pd
import matplotlib.pyplot as
 
 plt

df_train = pd.read_csv('../train_sample_10000000.csv')
    # 讀入檔案

## 畫分佈圖
statis_values = df_train['place_id'].value_counts().values
    # 統計地點id
place_statis = Series(statis_values, index = range(len(statis_values)))
    # 為地點id重新編號
place_statis.plot()
    # 繪圖
plt.show()
    # 顯示

## 資料統計描述
print(descirbe(df_train))
 

以下是抽樣資料大致的概貌情況：

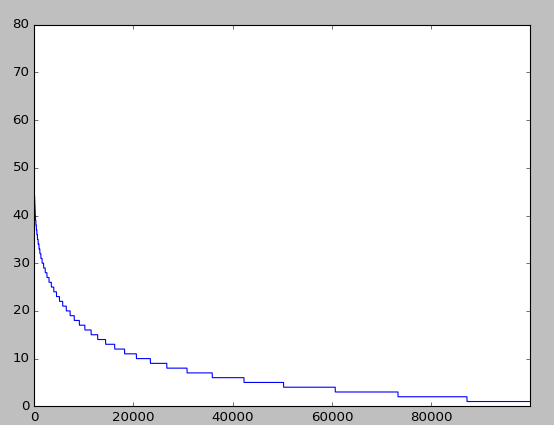
圖1：100,000個地點的頻數分佈

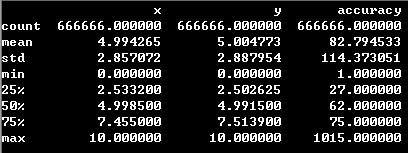
圖2：特徵的統計特性

如上圖所示：由於需要預測的類別集合元素有100,000個，故這種情況不適合使用迴歸、SVM、神經網路以及決策樹等演算法直接構建分類器。因為這些演算法僅僅在類別數目比較少時才能有效工作。

2.2 問題分解

2.2.1 抽樣問題：

由以上觀察的資料結果，我們可以對訓練資料進行抽樣。鑑於訓練樣本集有大致2千多萬條條目，故抽樣資料不能夠太少，否則會使得抽樣後的樣本分佈對比原分佈改變太多。
以下是抽樣函式的實現程式碼：

## 抽樣資料集
def pickSample(filename, nSample = 1000000):    
    df = pd.read_csv(filename)
    len_df = len(df.index)
    samp_id = sorted(random.sample(range(len_df), nSample))
        # 得到隨機的抽樣id
    outputFilename = filename[len(PATH_SAVE) : -4] + '_' + 'sample' + '_' + str(nSample) + '.csv'
        #　生成樣本資料的檔名
    samps_train = df[df.row_id.isin(samp_id)]
    samps_train.to_csv(PATH_SAVE + outputFilename, index = False, mode = 'w')   

pickSample('../train.csv', 1000000)
    # 抽取1000000個訓練樣本

2.2.2 地理座標網格化：

由於訓練資料與預測資料的條目非常多，對於任何一個機器學習演算法都是一個不小的負擔。特別對於在這個地方，嘗試通過將x，y地點切分為40*40網格的方型區域，隨機其中選取中一個網格進行資料探索。

## 將資料分到相應的網格中去
    n_cell_x = 40
    n_cell_Y = 40

    # x, y尺度歸一
    size_x = 10. / n_cell_x
    size_y = 10. / n_cell_y

    ## 去除0值
    eps = 0.00001 # 設定精度到eps，
    xs = np.where(df.x.values < eps, 0 , df.x.values - eps)
    ys = np.where(df.y.values < eps, 0 , df.y.values - eps)

    ## 生成網格id
    pos_x = (xs / size_x).astype(np.int)
        # normilze and change it to int type(整數)
    pos_y = (ys / size_y).astype(np.int)
    df['grid_cell'] = pos_y * n_cell_x + pos_y

    ## 試驗
    th = 5 # 地點頻數閾值
    test = getDataFromGrid(df_train, 0, th)

##　網格內資料擷取
def getDataFromGrid(df, grid_id, th):
    df = df.loc[df.grid_cell == grid_id]
        # 與 temp = df[df.grid_cell == grid_id] 等價
        # 擷取滿足條件的train樣本
    place_counts = df.place_id.value_counts()
        # 做每個網格里的地點統計
    mask = (place_counts[df.place_id.values] >= th).values
        # 將數目少的地點當做噪聲排除掉
        # 這裡dfInCell_train.place_id.values作為下標輸入，輸出的該地點下標
        # 的統計值
    df = df.loc[mask]

    return df

分佈圖如下所示：

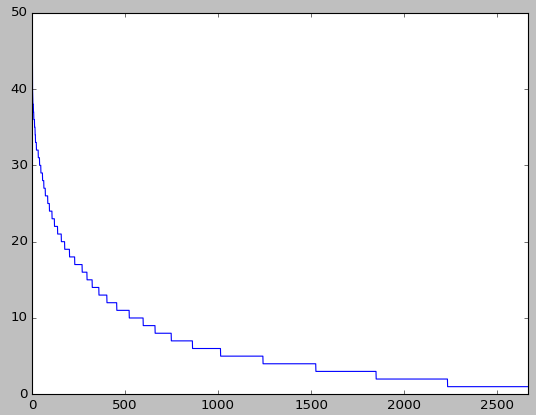
圖3：某個網格內的地點頻數分佈

可以看出，隨機選取的網格中的地點數量降至2600多。可以發現100,000個地點確實是按一定地理位置分佈的。故選擇合適的網格大小在按網格劃定建立每個網格對應的預測系統是可行的。同時地點中有許多頻數非常小的地點，這些地點在預測中通常對被預測系統的選擇推薦的可能性不大，故可將低於一定頻度的地點濾去。上面的做法對於使用如knn、貝葉斯以及其他ML演算法而言，較小的資料量能大幅減少演算法的訓練時間與空間儲存大小。

2.3 特徵分析：

給定的資料中有四個特徵：x，y，accuracy與time：以下依次為四個特徵的頻率分佈圖，前兩個圖為time與accuracy，後三個圖為想x，y的聯合分佈圖。

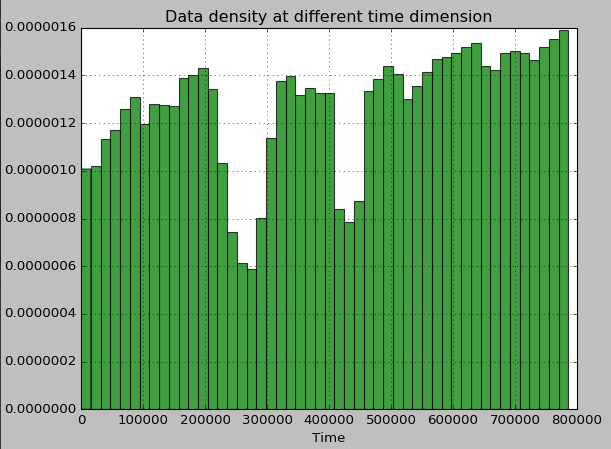
圖4：某個網格內的time頻數分佈

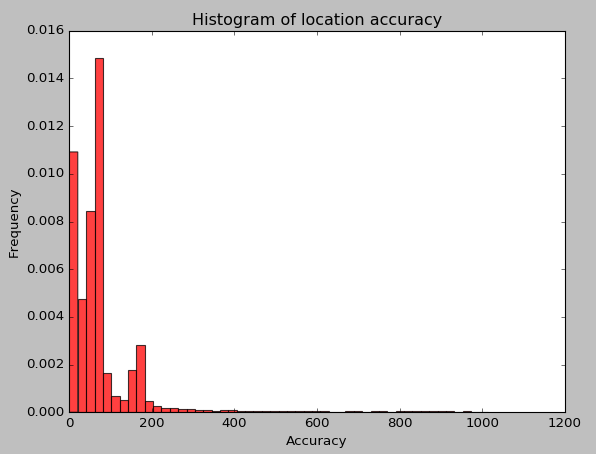
圖5：某個網格內的accuracy頻數分佈

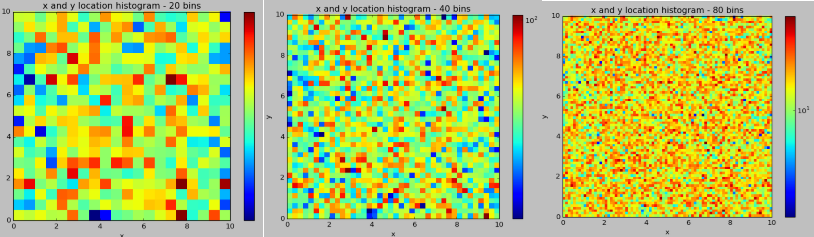
圖6：某個網格內x，y按20 X 20、40X40與80X80的樣本頻數分佈

由上圖可以觀察出幾個特徵之間的量程範圍差距太多，其中時間特徵需要具體切分細化。accuracy這個特徵取值的拖尾很嚴重，如果直接使用該特徵作為輸入，大多數ML演算法都會大打折扣。而且從網格化的x，y聯合分佈來看，其頻數分佈隨機性比較大，且其分佈並不是稠密的。故使用ML演算法去訓練資料時，需要考慮一些網格本身的樣本稀疏性，才能夠提供很好的地點預測。

其中繪圖的原始碼參考來自以下kaggle選手的公開程式碼：

2.4 資料預處理與特徵工程

以下是隨機擷取5個樣本資料，由於特徵有限，故可以考慮人工新增一些特徵:

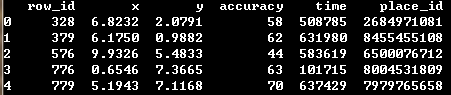
圖7：樣本示例

## 特徵生成函式
def featEngineering(df, n_cell_x, n_cell_y):

    ##　網格位置特徵
    size_x = 10. / n_cell_x
    size_y = 10. / n_cell_y

    eps = 0.00001 # 設定精度到eps，
    xs = np.where(df.x.values < eps, 0 , df.x.values - eps)
    ys = np.where(df.y.values < eps, 0 , df.y.values - eps)

    pos_x = (xs / size_x).astype(np.int)
        # normilze and change it to int type(整數)
    pos_y = (ys / size_y).astype(np.int)
    df['grid_cell'] = pos_y * n_cell_x + pos_y

    ## 修正地理特徵
    fw_1 = [500, 1000]
        # 特徵加權引數
    df.x = df.x.values * fw_1[0]
    df.y = df.y.values * fw_1[1]

    ## 時間特徵
    fw_2 = [4, 3, 1./22., 2, 10] 
    initial_date = np.datetime64('2014-01-01T01:01', dtype='datetime64[m]') 
    d_times = pd.DatetimeIndex(initial_date + np.timedelta64(int(mn), 'm') 
                               for mn in df.time.values)    
    df['hour'] = d_times.hour * fw_2[0]
    df['weekday'] = d_times.weekday * fw_2[1]
    df['day'] = (d_times.dayofyear * fw_2[2]).astype(int)
    df['month'] = d_times.month * fw_2[3]
    df['year'] = (d_times.year - 2013) * fw_2[4]
    df = df.drop(['time'], axis=1) 

    return df

從樣例資料中可以看出time採用的不是傳統的記錄形式，可將其轉化為年月日-時分秒的形式，再依次得到year，month，weekday，day，hour等更精確的時間特徵；對於各種精確時間可將其相對化，可生成hour_of_day，day_or_week，month_of_year等特徵；同時為了將樣本進行網格化，可以根據x，y的取值劃定其處於哪個網格，並設為新特徵grid_id；accuracy特徵由於其分佈呈現拖尾情況，故可以新增其對數特徵作為新特徵。

3、機器學習演算法：KNN

3.1 具體方案

資料切分為20*40個網格區域，使用網格化下的最近鄰演算法為每個預測樣本選取3個最有可能的地點。KNN演算法在每個網格中使用，以下是使用25個k鄰近點、採用距離加權，且距離度量為曼哈頓距離的knn程式碼（KNN的演算法來自scikit-learn的python機器學習包）：

    nNeighbors = 25
    clf = KNeighborsClassifier(n_neighbors = nNeighbors, weights='distance', 
                                metric='manhattan')
    clf.fit(X, y)
    y_pred = clf.predict_proba(X_test)

3.2 實現程式碼

• 網格內的knn演算法：

def knn_inGrid(df_train, df_test, grid_id, th, mpps): 

    grid_train = getDataFromGrid(df_train, grid_id, th)
    grid_test = df_test.loc[df_test.grid_cell == grid_id]

    canPass = len(grid_train) != 0 and len(grid_test) != 0

    if canPass == True:
        print('one grid use knn')
        ## 提煉訓練與測試樣本資料  
        row_ids = grid_test.index
            # 獲得id

        ## 機器學習模組
        le = LabelEncoder()
            # 生成一個標籤編碼器，利用標籤編碼器給多個類做編碼
        y = le.fit_transform(grid_train.place_id.values)
            # 轉換成輸出y
        X = grid_train.drop(['row_id', 'place_id', 'grid_cell'], axis=1).values.astype(int)
            # 一步到位轉化成ndarry，可以作為機器學習演算法輸入
        X_test = grid_test.drop(['row_id', 'grid_cell'], axis = 1).values.astype(int)

      ## 演算法

        nNeighbors = 25
        clf = KNeighborsClassifier(n_neighbors = nNeighbors, weights='distance', 
                                    metric='manhattan', n_jobs = -1)
        clf.fit(X, y)
        y_pred = clf.predict_proba(X_test)
        pred_labels = le.inverse_transform(np.argsort(y_pred, axis=1)[:,::-1][:,:3])  
            # 排序可能性由高到低，轉化標籤
            # [:,::-1]是取反序（兩個分號），[:,:3]是擷取前3個   

    ## 如果網格內無訓練資料，但有測試資料。使用最頻繁的地點id填充       
    elif len(grid_test) != 0:
        print('one grid use mpps')
        row_ids = grid_test.index
        pred_labels = np.array([np.array(mpps) for i in range(len(row_ids))])

    ## 若果網格內訓練集與測試集都沒有  
    else:
        pred_labels = False
        row_ids = False
        print('skip one grid')
        pdb.set_trace()

    return pred_labels, row_ids



def knn(df_train, df_test, th, n_cells):
    preds = np.zeros((df_test.shape[0], 3), dtype=np.int64)
    mpps = getMostProbPlaces(df_train)

    for grid_id in range(n_cells):
        if grid_id % 100 == 0:
            print('finish: %s grids' %(grid_id))
        pred_labels, row_ids = knn_inGrid(df_train, df_test, grid_id, th, mpps) 
        if isinstance(pred_labels, np.ndarray) == False:
            continue
        else:
            preds[row_ids] = pred_labels
        # 保留下測試集的標籤
    return preds

• 主函式部分：

df_train = featEngineering_ver1(df_train, n_cell_x, n_cell_y)
df_test = featEngineering_ver1(df_test, n_cell_x, n_cell_y)

## training and predicting
preds = knn(df_train, df_test, th, n_cell_x * n_cell_y)

使用KNN演算法需要考慮的是特徵之間的量程問題，太大量程範圍的特徵會對演算法起主導作用。故使用需要改變各個特徵的加權引數，使用加權引數可以將各個特徵量程調節到大致的水平上，但是這樣忽略了不同特徵的重要性。為了發掘不同特徵並做加權引數的確定，我們使用邏輯迴歸的方法可以大致估算knn演算法的權重，具體思路如下：

由於採用的是曼哈頓距離，且採用距離加權，可以想象KNN此時的分類的決定因素是樣本點與鄰近點的距離。故可以考慮一個機器學習問題：對於一個給定的地點ID，設計一個二分類器，分類輸出結果為是此地點和非此地點，而輸入的特徵為鄰近點的特徵與樣本點特徵的差值。使用常用機器學習方法可解決此機器學習問題，該方案中採用邏輯迴歸，而得到的權值即可作為KNN演算法的特徵加權參考值。

輸入特徵為x，y，hour，day_of_week，month_of_year，year，下面為計算程式碼塊：

    df['hour'] = d_times.hour
    df['weekday'] = d_times.weekday
    df['month'] = d_times.month

    df['hour'] = (d_times.hour%24+1)*fw[2]
    df['weekday'] = (df['weekday']%7+1)*fw[3]
    df['month'] = (df['month']%12+1)*fw[4]
    df['year'] = (d_times.year - 2013) * fw[5]

加權引數計算程式碼：<待補充>
得到的KNN加權依次為:

knn_w = [500., 1000., 3., 4., 3., 11.]

以上的方案的評估結果分數為：0.56829

3.3 演算法提升

3.3.1 更精細的特徵工程

再加入了3維特徵，accuracy的對數值特徵，sine與cos值特徵

    df['sine'] = np.sin(2*np.pi*df["hour_of_day"]/24)
    df['cos'] = np.cos(2*np.pi*df["hour_of_day"]/24)
    df['accuracy'] = np.log(df['accuracy']+1)

得到的KNN加權依次為:

knn_w = [500., 1000., 4., 3., 2., 11., 10., 12., 9.]

得到的結果為：（待補充），提升了一些。

3.3.2 彌補網格化的缺陷

網格化的KNN沒有考慮到如下的問題，當要預測的網格邊界附近的樣本點時，其附近的近鄰點有可能很多在網格邊界之外，而網格化的KNN演算法並沒有考慮到這些點，從而導致網格邊界附近的樣本點預測效果比較差。

這裡的方案參考kaggle選手 David 的方案，採用網格鬆弛增量的方式緩解這個問題。具體方案：

對訓練資料進行網格化資料擷取時，定義x，y兩個方向上的鬆弛增量。在擷取長寬均比原網格較大的網格，再資料輸入KNN演算法模組訓練。這樣做減少如左圖所示的邊界問題出現的可能情況。對於測試資料採用非鬆弛增量的方式擷取資料即可，並利用上面得到的KNN模組進行預測。

由於太多的特徵超出了8G RAM，機器跑不了，故僅選擇如下的特徵：

x，y，hour，day_of_week，month_of_year，year

計算得到的相應權值為：

knn_w = [500., 1000., 3., 4., 3., 11.]

擷取的程式碼如下：

    x_border_augment = 0.02
    y_border_augment = 0.02
    #Working on df_train
    df_cell_train = df_train[(df_train['x'] >= x_min-x_border_augment) & (df_train['x'] < x_max+x_border_augment) &
                               (df_train['y'] >= y_min-y_border_augment) & (df_train['y'] < y_max+y_border_augment)]
    #Working on df_test
    df_cell_test = df_test[(df_test['x'] >= x_min) & (df_test['x'] < x_max) &
                               (df_test['y'] >= y_min) & (df_test['y'] < y_max)]

計算結果為：0.57187

3.3.2 Ensemble方法提升預測精度

<未完>

以上的程式碼和思路參考以下選手的程式碼與資料：