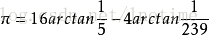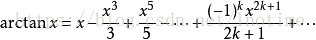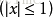馬青公式：

再根據

得到

π = 16(1/5 - 1/3/5^3 + 1/5/5^5 - ...) - 4(1/239 - 1/3/239^3 + 1/5/239^5 - ...)

π = (16/5 - 4/239) + (- 16/5^3/3 + 4/239^3/3) + (16/5^5/5 - 4/239^5/5) + ...

這就可以計算每一項，再累加即可。由於浮點數的小數位數有限，所以用整數來計算π，比如想計算小數點後10位，就直接計算乘以10^10後的結果，那就是上面那個式子等號右邊擴大10^10倍。當數值特別大但型別是浮點型別的時候會用科學計數法表示，也會損失精度，所以除法都用取模防止得到浮點數。

def pi(n):
    p = 10 ** (n + 10)  # 準備初始整數，先多乘10個0，以增加精度，最後再去掉
    a = p * 16 // 5     # 第一項的前半部分
    b = p * 4 // -239   # 第一項的後半部分
    f = a + b           # 第一項的值
    p = f               # π
    j = 3              
    while abs(f):       # 當|f|=0後計算π的值就不會再改變了
        a //= -25       # 第n項的前半部分
        b //= -57121    # 第n項的後半部分
        f = (a + b) // j
        p += f
        j += 2
    return p // 10**10
 

第一句的多乘10個0，也是為了增加精度，隨著n的增大，總會有不準確的時候。當多乘1、2、3...9個0時，分別計算到小數點後第 8, 31, 158, 306, 359, 4254, 13389, 17533, 17533 位開始不準確，當多乘10個0時，一直計算十萬位都沒有出現錯誤。