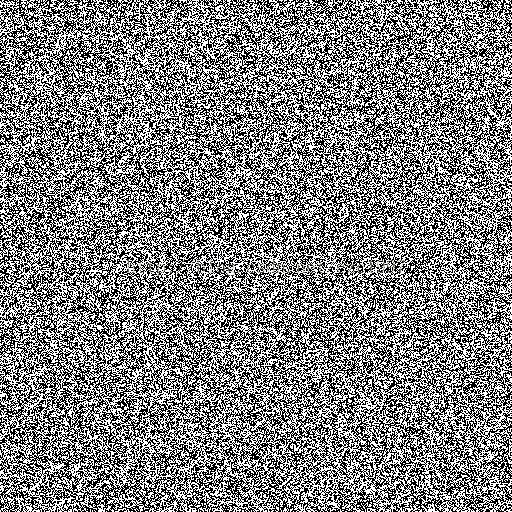說到隨機這個詞，相信各位肯定都深有體會了。生活中有太多的不確定因素從各方各面影響著我們，但也正是因為這樣我們的人生更加多彩，具有了更多的可能性。

可以說，隨機是個非常有魅力的東西。

你在生活中可能因為隨機享過福，也有可能吃過虧。想要對它瞭解更多？如今是時候去揭開它的真面目了。

I.真隨機數&偽隨機數的基本定義

在這之前需要先明白一點：隨機數都是由隨機數生成器（Random Number Generator）生成的。

1.真隨機數 TRUE Random Number

真正的隨機數是使用物理現象產生的：比如擲錢幣、骰子、轉輪、使用電子元件的噪音、核裂變等等，這樣的隨機數發生器叫做物理性隨機數發生器，它們的缺點是技術要求比較高。      ----百度百科

根據百科上的定義可以看到，真隨機數是依賴於物理隨機數生成器的。使用較多的就是電子元件中的噪音等較為高階、複雜的物理過程來生成。

至於“宇宙中不存在真正的隨機”這種言論已經屬於哲學範疇，在此不做討論。在此我們預設存在隨機。

使用物理性隨機數發生器生成的真隨機數，可以說是完美再現了生活中的真正的“隨機”，也可以稱為絕對的公平。

2.偽隨機數 Pseudo-Random Number

真正意義上的隨機數（或者隨機事件）在某次產生過程中是按照實驗過程中表現的分佈概率隨機產生的，其結果是不可預測的，是不可見的。而計算機中的隨機函式是按照一定演算法模擬產生的，其結果是確定的，是可見的。我們可以這樣認為這個可預見的結果其出現的概率是100%。所以用計算機隨機函式所產生的“隨機數”並不隨機，是偽隨機數。

---百度百科

從定義我們可以瞭解到，偽隨機數其實是有規律的。只不過這個規律週期比較長，但還是可以預測的。主要原因就是偽隨機數是計算機使用演算法模擬出來的，這個過程並不涉及到物理過程，所以自然不可能具有真隨機數的特性。

II.c語言中的偽隨機數詳解

既然我們已經瞭解了真偽隨機數的概念，接下來就來探究一下離我們最近的偽隨機數吧。

c語言中就存在一個隨機函式：rand().它就是一個標準的偽隨機數生成器。依賴的標頭檔案是stdlib.h.

接下來我就使用rand函式，來試著產生一些隨機數。

#include <stdio.h>
#include <stdlib.h>

int main ()
{
       int random = rand();
    printf("%d\n",random);
    random = rand();
    printf("%d\n",random);
    random = rand();
    printf("%d\n",random);
}
 

這裡我使用一個整形變數來接受rand函式產生的隨機數，並對其進行列印。

執行後，成功看到了結果。貌似是一串隨機數。

可是，當我們多次執行時，發現它的數值卻還是41，18467, 6334。

這並不是我們想要的結果，我們希望每一次執行都可以產生不同的數值。可是如何解決這個問題呢？

其實，在c語言中的rand函式中有一個定義叫做種子，rand函式是通過對這個種子進行一系列的運算來模擬出一個隨機數的。我們直接呼叫rand函式，並不指定種子，系統就會呼叫預設的種子：1，來產生隨機數。因為每次重新執行時的種子都是1，執行出來的結果自然就還是這幾個數啦。

現在我們已經知道了種子這個重要的引數，我們就可以用一個一元二次方程來模擬這個過程。

例如，rand函式的內部實現為 x^2 + 4x - 8,這個種子就相當於x。

如果想要改變rand最終的值，只能通過改變x來實現。

那麼，既然要產生隨機數，x就應該是一直在不斷變化的，才能讓x^2 + 4x - 8這個表示式的值不斷的變化。

x，也就是種子，該採用什麼東西呢？

沒錯，最理想的就是時間了。時間每分每秒都在變動，正好符合我們的要求。這裡需要使用到time.h。

#include <stdio.h>
#include <time.h>
#include <stdlib.h>

int main ()
{
	srand ((unsigned)time(NULL));
	int random = rand();
	printf("%d\n",random);
	random = rand();
	printf("%d\n",random);
	random = rand();
	printf("%d\n",random);
}

這時候再執行，每次都會得出不同的結果了。

這裡srand函式的定義就是：隨機數生成器的初始化函式。通常是和rand函式配合使用的。

函式原型：srand(unsigned seed)

程式碼中的time（NULL）將返回計算機目前的時刻與1970年1月1日0時0分0秒之間的時間差，單位是秒。

srand又需要unsigned int型別，所以這裡使用一個強制型別轉換，最後完成種子的設定。

需要注意的是，srand函式必須放在迴圈或者迴圈呼叫的外面，否則還是會得出重複的數字。

到這裡，就可以產生你想要的隨機數了。如果你想在0~4之間產生隨機數，只需要int random = rand（）%4，這樣每次出來的隨機數就會在0-4中了。

那麼，我想讓產生的隨機數在1-100範圍內，用int random = rand（）%100，這樣行嗎？

當然不行！！

是，沒錯，結果都是在範圍內的。但是你如果短時間內連續執行，會發現它是有規律可循的，會隨著時間的推移慢慢上漲，到100後再回到0，再重新上漲...

這可是個嚴重的問題。遊戲如果敢這麼做，肯定會虧的妻離子散。

所以，這個辦法只能用於範圍較小的隨機數，應用範圍非常窄。

通用的一個方法是  （int）(n*rand()/(RAND_MAX+1.0))，這樣產生隨機數的週期會大大縮短，從而達到我們想要的效果。

III.真隨機數的詳解

之前已經介紹過，真隨機數是使用物理裝置產生的。那麼在這裡我就要介紹一個網站：

這個網站可以免費提供真隨機數的服務，並且可以自己設定上下限，通常用於重要場合。

那麼，既然偽隨機數生成那麼簡單，而且看上去確實是隨機的，為什麼人們還要大費周章的使用繁瑣又高價的物理裝置去獲得隨機數呢？

前面在偽隨機數的定義裡講了，偽隨機數其實是有周期的。

聽起來很恐怖對不對？也就是說，經過足夠多次的執行，結果會出現重複。

// Requires the GD Library
header("Content-type: image/png");
$im = imagecreatetruecolor(512, 512)
    or die("Cannot Initialize new GD image stream");
$white = imagecolorallocate($im, 255, 255, 255);
for ($y = 0; $y < 512; $y++) {
    for ($x = 0; $x < 512; $x++) {
        if (rand(0, 1)) {
            imagesetpixel($im, $x, $y, $white);
        }
    }
}		
imagepng($im);
imagedestroy($im);

這是摘自

的一段程式碼，使用PHP語言編寫的。它的作用就是將隨機數視覺化。下面分別放出真隨機數和偽隨機數的影象。

真隨機數影象：

偽隨機數影象：

很明顯的可以看到，偽隨機數的影象呈現出了某種規律。但作者也同時解釋到：這個現象也只是在Windows平臺上的php語言中的 rand函式裡出現。當他在linux上運行同樣的程式碼時，發現並沒有非常明顯的規律。同樣是windows平臺的PHP語言，使用mt_rand()這個改進了的隨機數生成函式的話也不會發現明顯的規律。

筆者推測是大大增加了重複的週期，畢竟是演算法產生的偽隨機數，永遠不可能具有真隨機數的不確定性。也就是說，規律還是存在，只不過需要更長的觀察週期 才能夠發現而已。

所以真隨機數的重要性就在於，完全沒有規律。所以一般企業對產品的加密祕鑰的生成必須採用真隨機數生成器，這樣才能保證萬無一失，杜絕了被破解的可能性。