官方地址：

http://cs231n.github.io/neural-networks-1/#actfun

翻譯：

這三天寫上

常用的啟用函式
每個啟用函式（或者非線性的）輸入一個數值然後對其作某個固定的數學處理。你在練習中可能遇到這些啟用函式。
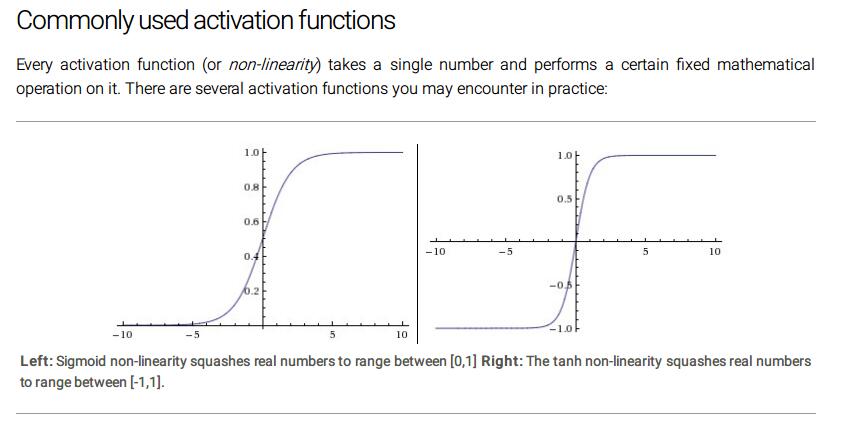
左：Sigmoid 非線性對映實數到[0,1]區間，右：tanh非線性對映實數到[-1,1]區間。
Sigmoid。sigmoid非線性啟用函式的公式是，如上上圖左。之前的章節提過，它將實數壓縮到0 1 區間。而且，大的負數變成0，大的正數變成1。sigmoid函式由於其強大的解釋力，在歷史上被最經常地用來表示神經元的活躍度：從不活躍（0）到假設上最大的（1）。在實踐中，sigmoid函式最近從受歡迎到不受歡迎，很少再被使用。它有兩個主要缺點：
1.sigmoid過飽和、丟失了梯度。sigmoid神經元的一個很差的屬性就是神經元的活躍度在0和1處飽和，它的梯度在這些地方接近於0。回憶在反向傳播中，某處的梯度和其目標輸出的梯度相乘，以得到整個目標。因此，如果某處的梯度過小，就會很大程度上幹掉梯度，使得幾乎沒有訊號經過這個神經元以及所有間接經過此處的資料。除此之外，人們必須額外注意sigmoid神經元權值的初始化來避免飽和。例如，當初始權值過大，幾乎所有的神經元都會飽和以至於網路幾乎不能學習。
2.sigmoid的輸出不是零中心的。這個特性會導致為在後面神經網路的高層處理中收到不是零中心的資料。這將導致梯度下降時的晃動，因為如果資料到了神經元永遠時正數時，反向傳播時權值w就會全為正數或者負數。這將導致梯度下降不希望遇到的鋸齒形歡動。但是，如果採用這些梯度是由批資料累加起來，最終權值更新時就會更準確。因此，這是一個麻煩一些，但是能比上面飽和的啟用問題結果好那麼一些。
Tanh.Tanh如上圖右。其將實數對映到[-1,1]。就像sigmoid神經元一樣，它的啟用也會好合，但是不像sigmoid函式，它是零中心的。因此在實際應用中tanh比sigmoid更優先使用。而且注意到tanh其實很簡單，是sigmoid縮放版。


左：糾正線性單元啟用函式，就是當x<0為0，當x>0時斜率為1。右：從Krizhevsky 等人論文中摘出的圖表，表現ReLU單元比tanh單元具有6倍的收斂速度提升。
ReLU。ReLU近幾年很流行。它求函式f(x) = max(0,x)。換句話說，這個啟用函式簡單設0為閾值（見上圖左—）。關於用ReLU有這些好處和壞處：
（+）其在梯度下降上比較tanh/sigmoid有更快的收斂速度。這被認為時其線性、非飽和的形式。
（+）比較tanh/sigmoid操作開銷大（指數型），ReLU可以簡單設計矩陣在0的閾值來實現。
（-）不幸的是，ReLU單元脆弱且可能會在訓練中死去。例如，大的梯度流經過ReLU單元時可能導致神經不會在以後任何資料節點再被啟用。當這發生時，經過此單元的梯度將永遠為零。ReLU單元可能不可逆地在訓練中的資料流中關閉。例如，比可能會發現當學習速率過快時你40%的網路都“掛了”（神經元在此後的整個訓練中都不啟用）。當學習率設定恰當時，這種事情會更少出現。


ReLU滲漏法。這是種解決ReLU掛了的辦法。當x<0，用小的負梯度(0.01)來替代0。

截圖存留：