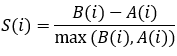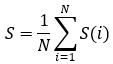聚類分析優缺點：

優點：

1.聚類是自動的不必帶有方向性

2.易於理解和實施

缺點：

1.有時候難以解讀聚類的結果

2.聚類結果對距離計算方式的算則和特徵之間的權重十分敏感

3.K-mean由K值主導

4.K-means對初始中心的選擇十分敏感

5.異常值也會成為族群

做聚類分析之前，我們要先對資料進行一些必要的處理：

對於continuous變數：

我們需要先rescale，把所有資料都化成同一口徑，才能進行比較。rescale一般採用兩種方法，一種是normalization，將資料統一變成0到1之間；另外一種方法是standardization，把資料都化成以0為mean，1為標準差的口徑。前者的缺點是若果存在異常值，會把正常的資料rescale到一個很小的範圍，後者則會變得unbounded。

對於categorical變數：

需要先變成0,1變數，如果種類多於2個，則需要創造dummy variable。

判斷k值的兩個方法：

1.根據經驗判斷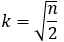，其中n是記錄數，因此k可能會很大

2.通過Silhouette值來判斷聚類的效果好壞，Silhouette介乎於-1到1之間，-1代表效果極差，1代表效果極好

Silhouette是一個判斷聚類效果的工具，其融合了一個族群內部的凝聚度以及族群於族群之間的分離度作為一個綜合指標。Silhouette的值在-1和1之間，數值越大，聚類效果越好。公式如下：

其中，S(i)表示每個點的Silhouette值，A(i)表示i這個點與其所屬族群所有點的距離平均值，B(i)表示i這個點與其中一個外族群中所有點的距離平均值的最小值(也就是說B(i)=min[ (i與第一個外族群所有點的距離平均值)，(i與第二個外族群所有點的距離平均值)，(i與第三個外族群所有點的距離平均值).....]，計算所有S(i),取平均值，

若果對於Silhouette的計算量太大，我們可以採取折中的方法，採取一種叫Slight Silhouette的方法來計算Slight Silhouette值用於判斷聚類效果。Slight Silhouette中A(i)的值是計算i這個點與本族群中心的距離，B(i)則是計算i到外族群中心點距離的最小值(即min(i與各個外族群中心點的距離))。