【BZOJ 2395】 [Balkan 2011]Timeismoney
2395: [Balkan 2011]Timeismoney
Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 304 Solved: 169
[Submit][Status][Discuss]
Description
有n個城市(編號從0..n-1),m條公路(雙向的),從中選擇n-1條邊,使得任意的兩個城市能夠連通,一條邊需要的c的費用和t的時間,定義一個方案的權值v=n-1條邊的費用和*n-1條邊的時間和,你的任務是求一個方案使得v最小
Input
第一行兩個整數n,m,接下來每行四個整數a,b,c,t,表示有一條公路從城市a到城市b需要t時間和費用c
Output
【output】timeismoney.out
僅一行兩個整數sumc,sumt,(sumc表示使得v最小時的費用和,sumc表示最小的時間和) 如果存在多個解使得sumc*sumt相等,輸出sumc最小的
Sample Input
5 7
0 1 161 79
0 2 161 15
0 3 13 153
1 4 142 183
2 4 236 80
3 4 40 241
2 1 65 92
Sample Output
279 501
HINT
【資料規模】
1<=N<=200
1<=m<=10000
0<=a,b<=n-1
0<=t,c<=255
有5%的資料m=n-1
有40%的資料有t=c
對於100%的資料如上所述
最小乘積生成樹模板題。
最小乘積生成樹:
每條邊有兩個權值
我們把
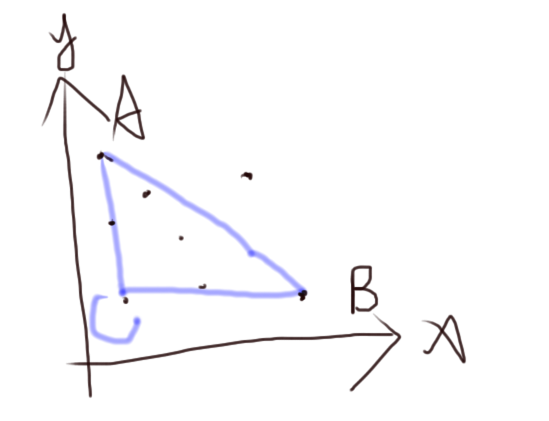
因此我們需要求出所有這些點構成的凸包的左下部分,從中找一個最大的。
怎麼求凸包的左下部分呢?
用分治法。
1.首先分別求出
2.然後遞迴下去分別求離
3.最後整個左下凸包上的點就都求出來了。
如何求離線段
離
我們要讓前面那一部分最小,那麼把所有邊權賦值為
邊界就是
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#define LL long long
using namespace std;
int n,m,f[205];
struct edge
{
int x,y,t,c;
LL v;
}e[100005];
struct Point
{
LL x,y;
}ans,A,B;
bool cmp(edge a,edge b)
{
return a.v<b.v;
}
int Getfather(int x)
{
return f[x]==x?x:f[x]=Getfather(f[x]);
}
Point Kruscal()
{
Point p=(Point){0,0};
sort(e+1,e+1+m,cmp);
for (int i=1;i<=n;i++)
f[i]=i;
int now=1;
for (int i=1;i<=m;i++)
{
int fx=Getfather(e[i].x),fy=Getfather(e[i].y);
if (fx==fy) continue;
p.x+=e[i].c,p.y+=e[i].t;
f[fx]=fy;
now++;
if (now==n) break;
}
if ((ans.x*ans.y==p.x*p.y&&p.x<ans.x)||ans.x*ans.y>p.x*p.y)
ans=p;
return p;
}
LL Cross(Point a,Point b,Point c)
{
return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
void Solve(Point a,Point b)
{
LL y=a.y-b.y,x=b.x-a.x;
for (int i=1;i<=m;i++)
e[i].v=1LL*e[i].c*y+1LL*e[i].t*x;
Point p=Kruscal();
if (Cross(p,a,b)>=0) return;
Solve(a,p);
Solve(p,b);
}
int main()
{
ans.x=1e9,ans.y=1e9;
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].c,&e[i].t),
e[i].x++,e[i].y++,e[i].v=e[i].c;
A=Kruscal();
for (int i=1;i<=m;i++)
e[i].v=e[i].t;
B=Kruscal();
Solve(A,B);
printf("%lld %lld\n",ans.x,ans.y);
return 0;
}